ROSSBY WAVES WITH THE CHANGE OFβAND THE INFLUENCE OF TOPOGRAPHY IN A TWO-LAYER FLUID
SONG Jian,LIU Quan-sheng,CEN Rui-ting,YANG Lian-gui
(1.College of Sciences,Inner Mongolia University of Technology,Hohhot 010051,China)(2.School of Mathematical Sciences,Inner Mongolia University,Hohhot 010021,China)
ROSSBY WAVES WITH THE CHANGE OFβAND THE INFLUENCE OF TOPOGRAPHY IN A TWO-LAYER FLUID
SONG Jian1,LIU Quan-sheng2,CEN Rui-ting1,YANG Lian-gui2
(1.College of Sciences,Inner Mongolia University of Technology,Hohhot 010051,China)(2.School of Mathematical Sciences,Inner Mongolia University,Hohhot 010021,China)
In this paper,we study the problem of the change of Rossby parameter and the topography in a two-layer fl uid.Based on the traveling wave method and the perturbation method,the Rossby wave amplitude is obtained to satisfy the homogeneous KdV equation and the homogeneous mKdV equation,which describe the evolution of the amplitude of solitary Rossby waves.The e ff ects of Rossby parameters and topography on Rossby wave are generalized.
change ofβ;homogeneous KdV equation;homogeneous mKdV equation;topography
1 Introduction
The solitary Rossby waves was applied to the planetary-scale wave phenomenon.Since Long[1]derived the Korteweg-de Vries(KdV)equation on a baratropic atmosphere,theories of solitary Rossby waves were developed by Larse[2],Benney[3-7],Clarke[8]and Redekopp[9,10]primarily in the context of the atmospheric models.The basic theory demonstrates that the amplitude of long Rossby waves propagating in a zonal shear flow is governed by either the KdV or modi fi ed Korteweg-de Vries(mKdV)equation depending on the vertical density distribution in the atmospheric model.Hukuda[11]studied the e ff ect of vertical shear in an analysis restricted to neutral modes propagating in a weak horizontal shear flow without critical layers.Pedlosky[12,13]presented theory that is the fi nite-amplitude behavior of unstable baroclinic waves in a quasi-geostrophic two-layer model,it was shown that in the absence of dissipation the equilibrated fi nite-amplitude state exhibits an oscillation,both of the mean flow and the baroclinic waves.Mitsudera and Grimshaw[14]also presented a weakly nonlinear,long-waves theory to describe a complicated system,they described thegeneration and evolution of mesoscale phenomena in a baroclinic current when it is interacting with a localized longshore topographic feature.Gottwald and Grimshaw[15]gave that the in fl uence of topography on the interaction of long,weakly nonlinear,quasigeostrophic baroclinic waves can be described by a pair of linearly coupled KdV equations,with a forcing term in one of the equations.Patoine and Warn[16]showed the interaction of long,quasi-stationary baroclinc waves with topography can be described by an inhomogeneous KdV equation.Liu and Tan[17]discussed the change of the Rossby parameter beta with latitude and extended the beta-plane approximation.Liu and Tan[18]used a barotropic semi-geostrophic model with topogrphic forcing the stability and solution of the nonlinear Rossby waves were discussed.They found that the e ff ect of the W-E oriented topography and the N-S oriented topography on the stability and phase speed of the waves are quite different,the Rossby waves forced by the topography can been described by the KdV equation.Luo[19]studied a kind of the solitary Rossby waves excited by the change ofβexcluding e ff ects of shear basic flow and topography,showed theβparameter with the change of latitude may be one reason of producing dipole blocking in the mid-high latitudes.Luo[20]investigated the planetary-scale baroclinic envelope Rossby solitons for zonal wavenumber 2 in a two-layer,it is found that when the shear of basic state westerly winds between the upper and lower layers is weak,both the upper-and lower-layer envelope Rossby solitons are almost in phase and exhibit vortex pair block structure which have a weak baroclinicity.But he did not discussed the topography e ff ect on the Rossby waves.Charney and Straus[21]showed that the forced flow of a barotropic fl uid over wary topography in a periodic beta-plane channel may possess a multiplicity of stationary equilibrium states of which more than one may be stable.Lv[22]showed the solitary Rossby waves caused by the shearing basic flow and orography with small variable slope were mainly of meridional wave number one and two,di ff erent shears of flow can excite di ff erent stream line patterns of solitary waves,and the orography with variable slope is also important factors of formation of solitary Rossby waves.Solutions of solitary waves play such an important role in soliton theory that many mathematicians and physicists were interested in this topic,such as Hirota’s bilinear method,the Jacobi elliptic function expansion method et al.[23,24]were proposed and used widely.
2 The Governing Equation
The non-dimensional quasi-geostrophic with topography potential vorticity equation in each fl uid layer on aβ-plane can be written in the form[11]
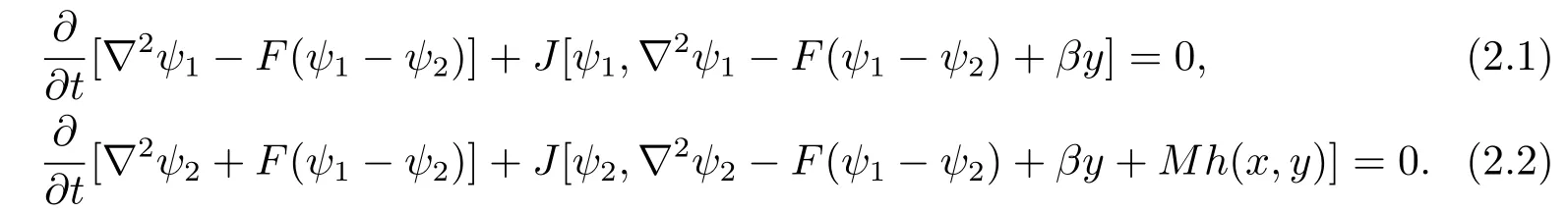
In equations(2.1),(2.2),the variables with subscripts 1,2 refer to the quantities defined in the upper and lower-layers,respectively.Theψn(x,y,t)represents the geostrophic streamfunction in the nth layer,wheren=1,2.?2is the horizontal Laplace operator,h(x,y)is the function of topography.The internal rotational Froude number and the dimensionless gradient of planetary vorticityβ,defined as
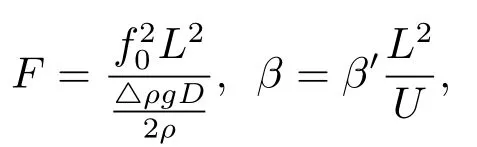
M=is the e ff ect parameter of topography,=gH,wheref0is a constant Coriolis parameter in moderate position,Lis the north-south extent of the zonal fi eld,the density di ff erence anomaly between the upper and lower layers,gthe gravitational acceleration,Dis the total fl uid depth andUis a characteristic zonal velocity,His the scale height.The boundary conditions is wall at the northern and southern[12]

Introducing a scaled coordinate in the form[9,10]

To consider e ff ects of topography,assuming[22],

herecis the phase speed of a long Rossby wave and?the dimensionless Rossby number assumed to be smaller than unity,it is a measure of the Rossby wave amplitude.Inserting(2.4)and(2.5)into(2.1),(2.2)and(2.3)gives an set of equations
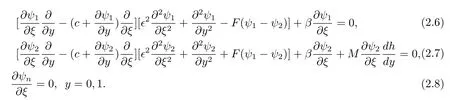
The total flowψ(ξ,y)is composed of the basic shear flow plus the long wave disturbance.
The disturbance turn out to be solitary waves described by nonlinear equation depending on the balance between the e ff ects of nonlinear and dispersion.
3 Expansion of Solution
3.1 The Even Order of?Expansion
First,we seek a solution in the form[25]
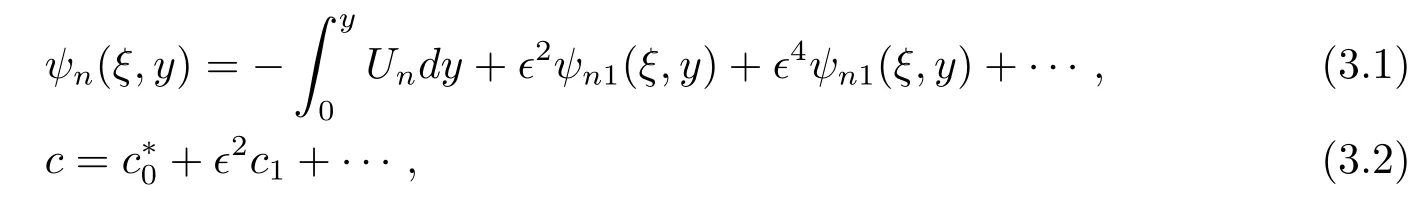
whereUn(y)represents a zonal in the nth layer,is the phase speed of an in fi nitely long Rossby wave.Inserting(3.1),(3.2)into(2.6),(2.7)gives
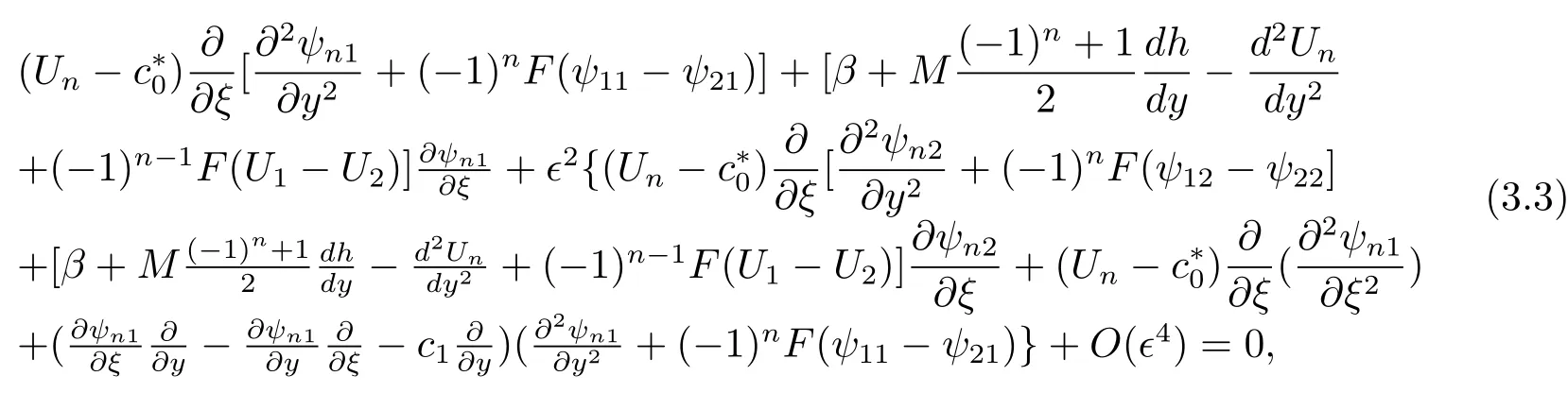
heren=1,2,from equation(3.3)the problem of the lowest order are written asO(?0):

Separating variables in the form[9]

whereφn(y)satis fi es
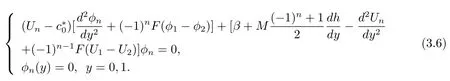
Equation(3.6)determines the model structure of a long Rossby wave while the wave amplitudeA(ξ)is as yet undetermined to this order.Proceeding to the next orderO(?2),obtainingO(?2):
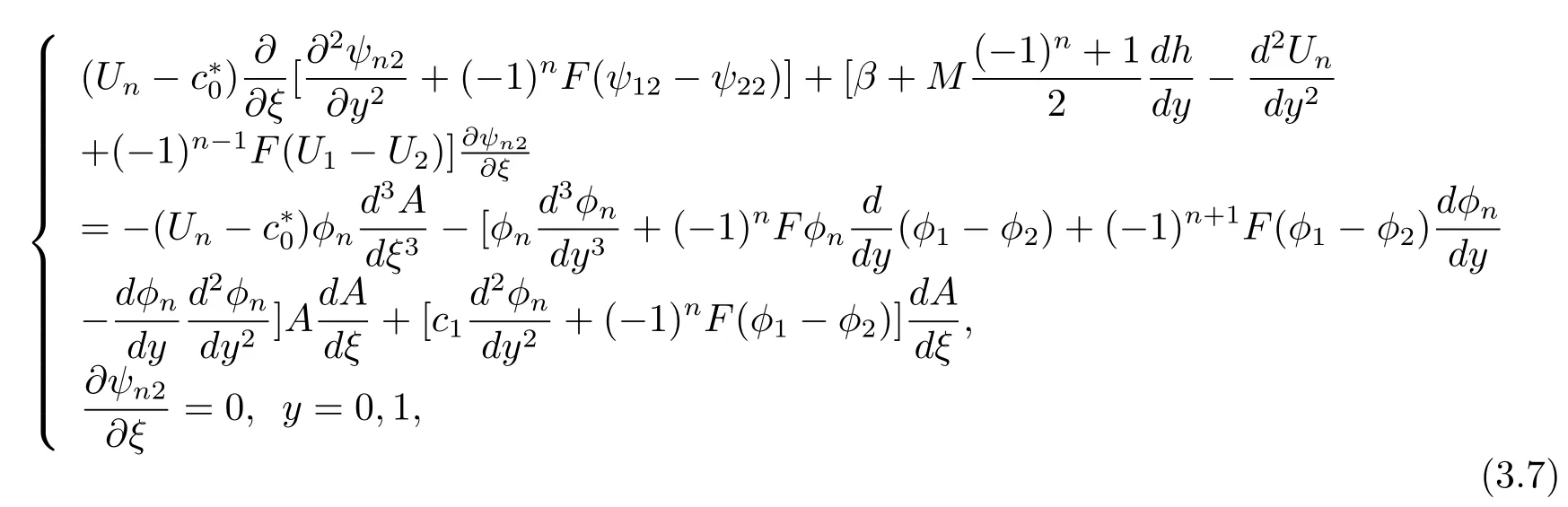
Using equation(3.6)gives

By application of the solvability condition having
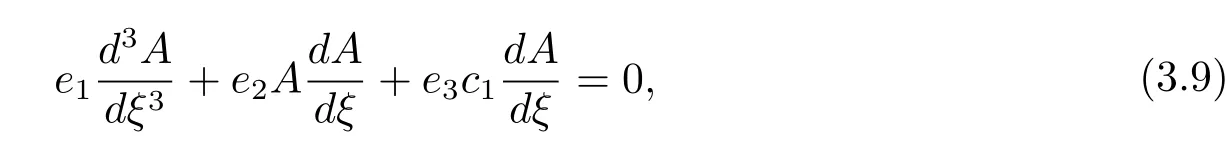
where

In the above derivation,assuming that any critical level does not exist,i.e.,Equation(3.9)is an KdV equation including topography forcing term.Pursuing
another possible expansion.
3.2 The Order of?Expansion
Another solution to equations(2.6)-(2.8)may be sought in the form
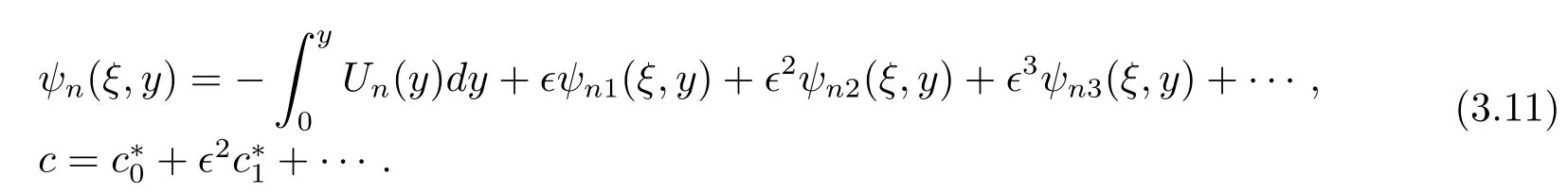
Substitution of(3.11)into equations(2.6),(2.7)yields
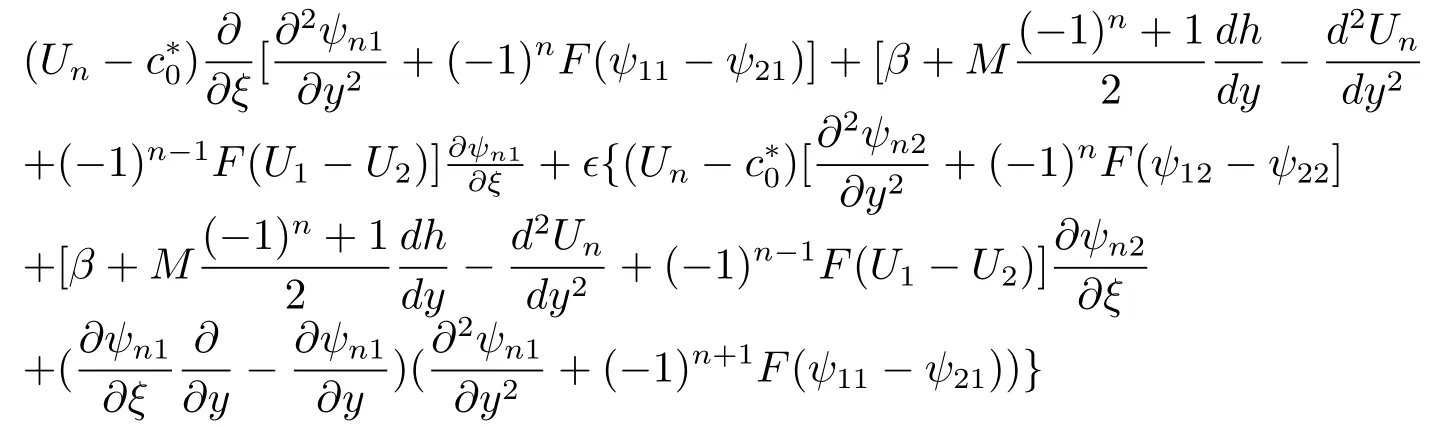
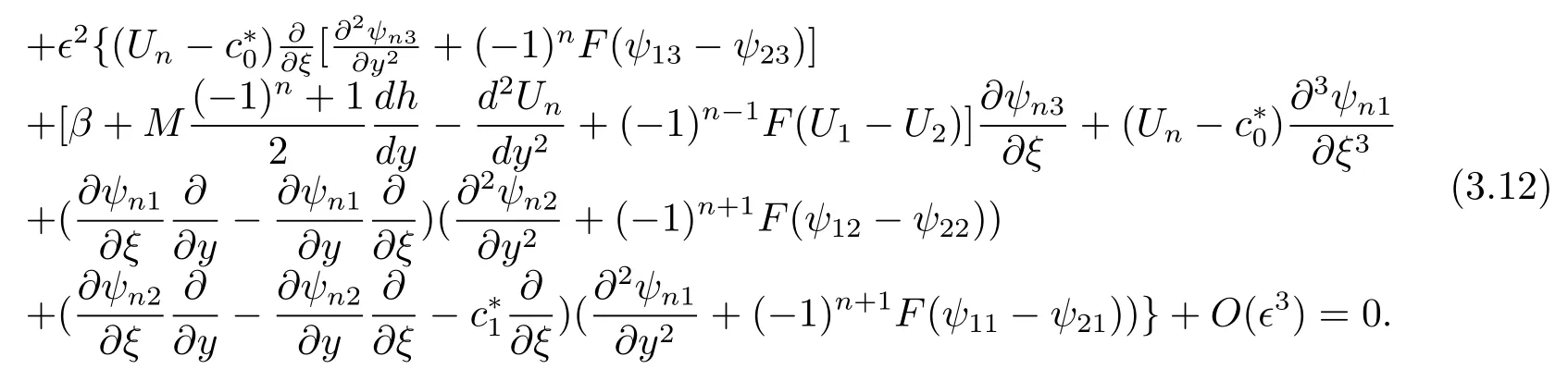
From equation(3.12),the problem of the lowest order are written asO(?0):
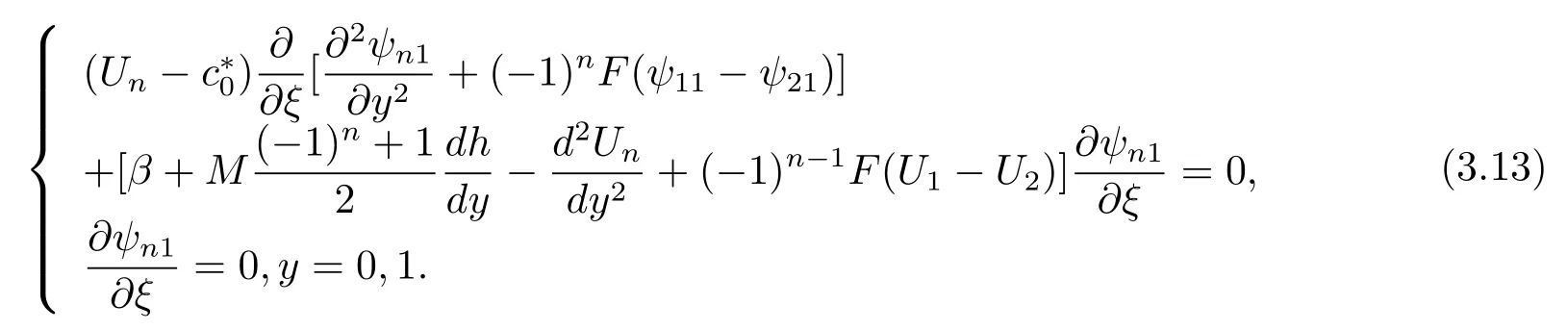
Separating variables in the form
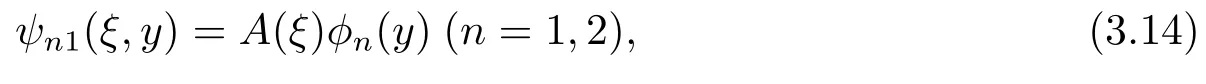
hereφn(y)satis fi es
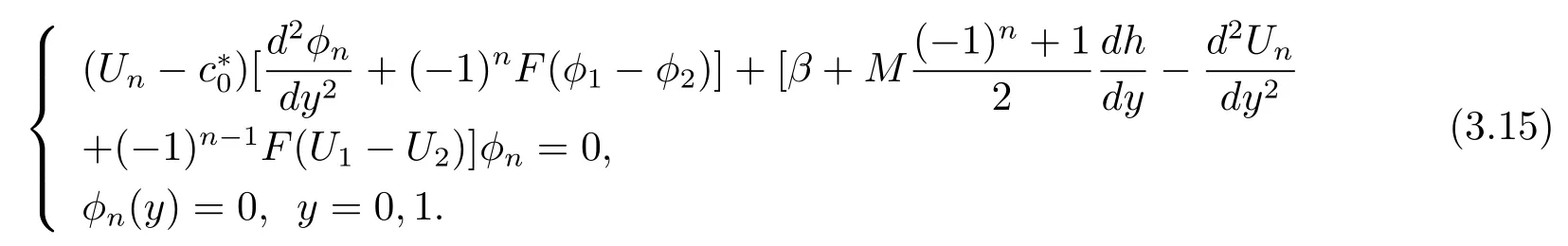
That the lowest order problem agrees with that of the KdV equation case.From the next order problem,we obtainO(?1):
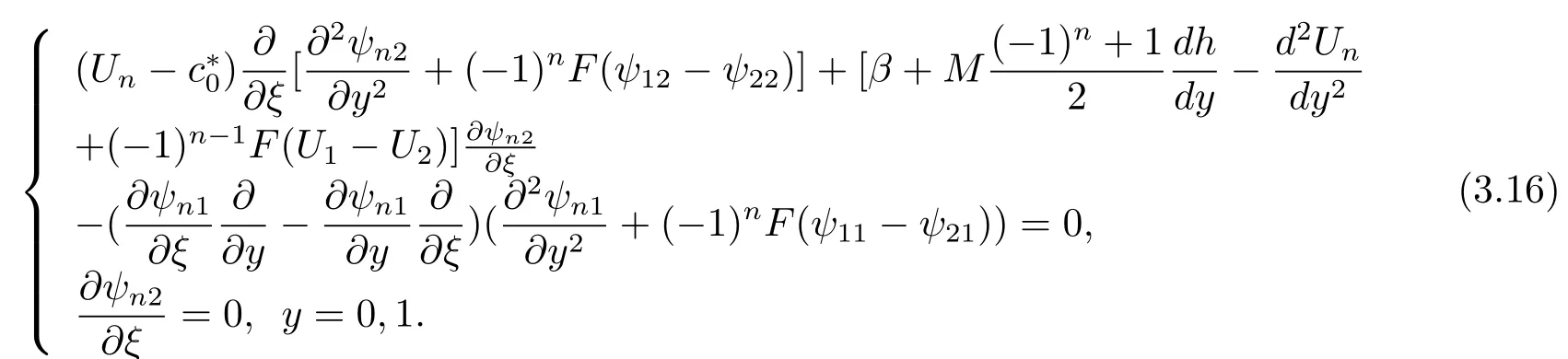
The solution of equation(3.16)is[11]

whereχn(y)satis fi es
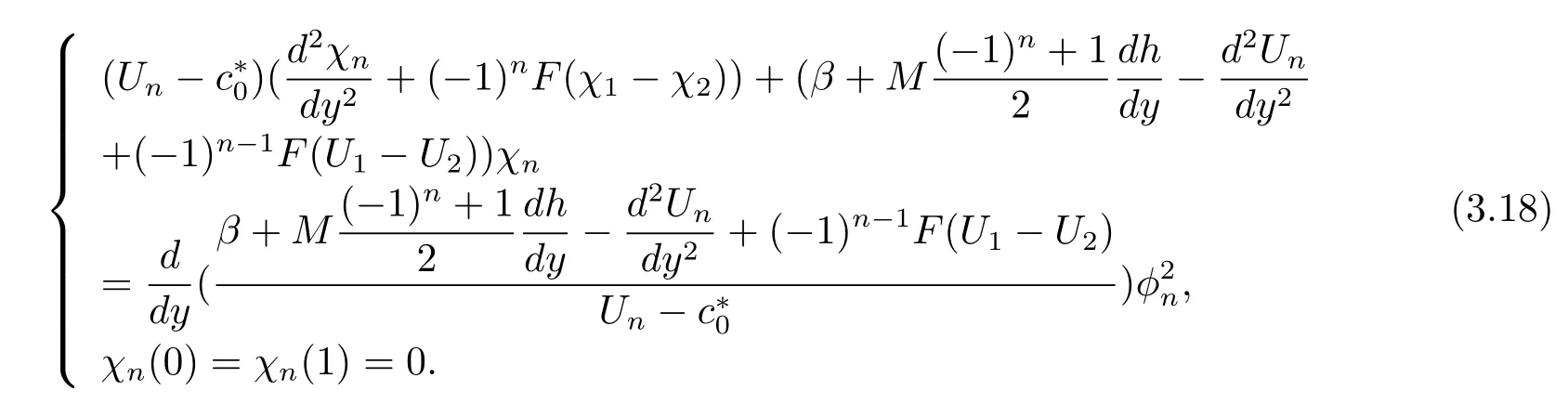
The last problem yieldsO(?2):

As in equation(3.8),application of the solvability condition yields,the mKdV equation
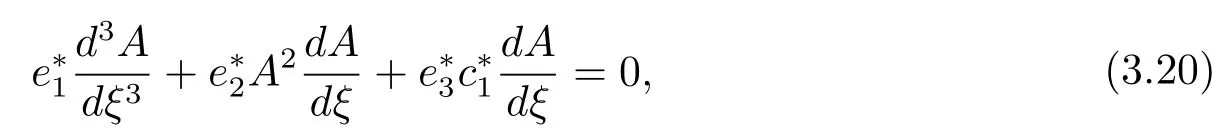
where
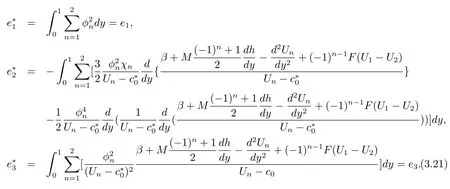
4 The Coefficient of KdV and mKdV Equation under the Change of β
In the section,discuss the change ofβand the topography.Theβand the topographic basic fi eld chosen here is[17,22]

The KdV equation has the solitary waves solution[11]
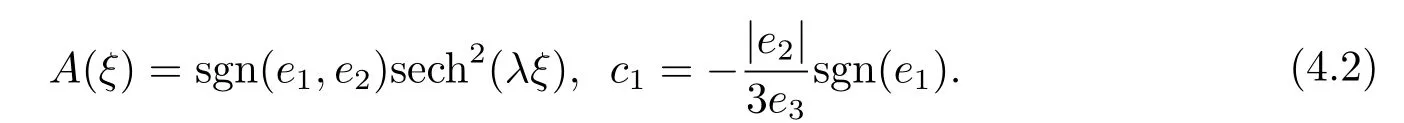
The wave steepnessλis
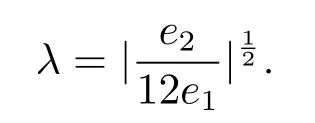
The solitary wave solution of the mKdV equation[11]
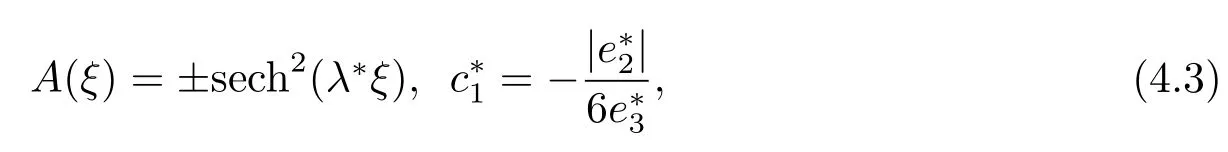
where

In order to determine these coefficients of the inhomogeneous KdV and mKdV equation,substitution of(4.1)into(3.10),(3.21),are approximate evaluated to yield

For the baroclinic modee2,tell us thatδ000 in spite of the absence of the basic flowUn=constant,the KdV(mKdV)solition can exist.The change ofβand topography is the important factors that induce Rossby solitary waves.
5 Concluding Remarks
These solitary Rossby waves of the two layer fl uid are described by the homogeneous KdV or mKdV equation depending on the baroclinicity fl uid,when the change ofβand the fl uid with the topography.In the general case where the basic flow has the shear,Rossby solitary waves are described by the KdV(mKdV)equation,but,if considering the change ofβ,the Rossby solitary can exit in the absence of horizontal shear in the basic flow.The inhomogeneous terms of the KdV and mKdV equation are induce by the bottom topography e ff ect.The internal rotational Froude numberFhas a certain e ff ect on the Rossby solitarywaves steepness,with the decrease ofF,the solitary waves steepness is increase.There is no e ff ect on the basic flow pattern of solitary waves.The horizontal shear and the vertical shear of the basic flow are also the factor causing solitary waves steepness increase.Finally,the further modi fi cations the Rossby waves will be considered;the instability of the Rossby solitary with the changeβ;the Rossby waves in then-level model.
[1]Long R.Solitart waves in the westerlies[J].J.Atmos.Sci.,1964,21(2):197-200.
[2]Larsen L N.Comments on :Solitary waves in the Westerlies[J].J.Atmos.Sci.,1965,22(2):222-224.
[3]Benney D J.Long nonlinear waves in fliud flow[J].J.Math.Phys.,1966,45(3):52-63.
[4]Benney D J.The e ff ect of latitudinal shear on equatorial waves.Part II:theory and methods[J].J.Atmos.Sci.,1978,35(12):2236-2258.
[5]Benney D J.Equatorial solitary waves.Part I:Rossby solitons[J].J.Phy.Ocean.,1980,10(11):1699-1717.
[6]Benney D J.Equatorial solitary waves.Part II:envelope solitons[J].J.Phy.Ocean.,1983,13(3):428-448.
[7]Benney D J.The slow manifold on a fi ve-mode model[J].J.Atmos.Sci.,1994,51(8):1057-1064.
[8]Clarke A.Solitary and cnoidal planetary waves[J].Geophys.Fluid Dyn.,1971,2(1):343-354.
[9]Redekopp L G.On the theory of solitary Rossby waves[J].J.Fluid Mech.,1977,82(4):725-745.
[10]Weidman P D and Redekopp L G.Solitary Rossby waves in the presence of vertieal shear[J].J.Atmos.Sci.,1980,37(8):2243-2247.
[11]Hisashi Hukuda.Solitary Rossby waves in a two-layer system[J].Tellus,1979,31(2):161-169.
[12]Pedlosky J.Finite-Amplitude baroclinic waves[J].J.Atmos.Sci.,1970,27(1):15-30.
[13]Pedlosky J.A simple model for nonlinear critical layers in an unstable baroclinic wave[J].J.Atmos.Sci.,1982,39(10):2119-2127.
[14]Mitsudera,Grimshaw.Generation of mesoscale variablility by Resonant interaction between a baroclinc current and localized topography[J].J.Phy.Ocean.,1991,21(6):737-765.
[15]Gottwald,Grimsaw.The e ff ect of topography on the dynamics of interacting solitary waves in the context of atmospheric blocking[J].J.Atmos.Sci.,1999,56(10):3663-3678.
[16]Patoine A,Warn T.warn the interaction of long,quasi-stationary baroclinic waves with topography[J].J.Atmos.Sci.,1982,39(5):1018-1025.
[17]Liu S K,Tan B K.Rossby waves with the change ofβ[J].Appl.Math.Mech.,1992,13(1):35-44(in Chinese).
[18]Liu S K,Tan B K.Nolinear Rossby waves Forced by topography[J].Appl.Math.Mech.,1988,9(3):229-240(in Chinese).
[19]Luo D H.Solitary Rossby waves with the beta parameter and dipole blocking[J].Quar.Appl.Meter.,1995,6(2):220-227(in Chinese).
[20]Luo D H.Planetary-scale baroclinic envelope Rossby solitons in a two-layer model and their interaction with synoptic-scale eddies[J].Dyna.Atmos.Ocean.,2000,32(1):27-74.
[21]Chraney J G and Straus D M.From-drag instability,multiple equilibria and propagating planetary waves in baroclinic,ographically force,planetary waves systems[J].J.Atmos.Sci.,1980,37(6):1157-1176.
[22]Lv K L.The e ff ects of orography on the solitary Rossby waves in a barotropic atmosphere[J].Acta Meter.Sin.,1987,45(3):267-420(in Chinese).
[23]Hu Zonghai,Wu Ranchao,Zhang Weiwei.Soliton solutions of the long-short wave resonance equations[J].J.Math.,2011,31(1):35-42.
[24]Li Ning,Taogetusang.The new solutions of some kinds of generalized nonlinear evolution equations[J].J.Math.,2014,61(1):7-14(in Chinese).
[25]Je ff rey A,Kawahara T.Asymptotic methods in nonlinear waves theory[M].Melbourne:Pitman Publishing Inc.,1982:22-26.
兩層流體中具有β變化和地形影響的Rossby波
宋 健1,劉全生2,岑瑞婷1,楊聯(lián)貴2
(1.內(nèi)蒙古工業(yè)大學(xué)理學(xué)院,內(nèi)蒙古呼和浩特 010051)(2.內(nèi)蒙古大學(xué)數(shù)學(xué)科學(xué)院,內(nèi)蒙古呼和浩特 010021)
本文研究了兩層流體中具有變化的Rossby參數(shù)和地形Rossby波的問題.利用行波法和攝動的方法,獲得了Rossby波振幅滿足齊次KdV方程和齊次mKdV方程,推廣了Rossby參數(shù)和地形對Rossby孤立波的影響.
變化的β;齊次KdV方程;齊次mKdV方程;地形
O351;P433
on:76B65;86A10
A Article ID: 0255-7797(2017)04-0751-10
date:2015-12-18Accepted date:2016-04-20
Supported by Natural Science Foundation of China(11362012;11562014);the scienti fi c research project of the Inner Mongolia Autonomous Region high school(NJZY16096);the Scienti fi c research project of Inner Mongolia University of Technology(ZD201411).
Biography:Song Jian(1970-),male,born at Xinzhou,Shanxi,assistance professor,major in geophysical fl uid dynamics dynamics.
——高建新教授
- 數(shù)學(xué)雜志的其它文章
- THE GROWTH ON ENTIRE SOLUTIONS OF FERMAT TYPE Q-DIFFERENCE DIFFERENTIAL EQUATIONS
- A MODIFIED BIC TUNING PARAMETER SELECTOR FOR SICA-PENALIZED COX REGRESSION MODELS WITH DIVERGING DIMENSIONALITY
- FINITE GROUPS WHOSE ALL MAXIMAL SUBGROUPS ARE SMSN-GROUPS
- GLOBAL BOUNDEDNESS OF SOLUTIONS IN A BEDDINGTON-DEANGELIS PREDATOR-PREY DIFFUSION MODEL WITH PREY-TAXIS
- ON PROJECTIVE RICCI FLAT KROPINA METRICS
- 態(tài)R0代數(shù)

