A PROJECTION-TYPE ALGORITHM FOR SOLVING GENERALIZED MIXED VARIATIONAL INEQUALITIES?
Kai TU(涂凱) Fuquan XIA(夏福全)
1.Department of Mathematic,Sichuan Normal University,Chengdu 610068,China
2.College of Applied Sciences,Beijing University of Technology,Beijing 100124,China
A PROJECTION-TYPE ALGORITHM FOR SOLVING GENERALIZED MIXED VARIATIONAL INEQUALITIES?
Kai TU(涂凱)1,2?Fuquan XIA(夏福全)1
1.Department of Mathematic,Sichuan Normal University,Chengdu 610068,China
2.College of Applied Sciences,Beijing University of Technology,Beijing 100124,China
E-mail:kaitu?02@163.com;fuquanxia@sina.com
We propose a projection-type algorithm for generalized mixed variational inequality problem in Euclidean space Rn.We establish the convergence theorem for the proposed algorithm,provided the multi-valued mapping is continuous and f-pseudomonotone with nonempty compact convex values on dom(f),where f:Rn→R∪{+∞}is a proper function.The algorithm presented in this paper generalize and improve some known algorithms in literatures.Preliminary computational experience is also reported.
projection-type algorithm;generalized mixed variational inequality;f-pseudomonotone mapping
2010 MR Subject Classifcation90C25;90C30;90C33
1 Introduction
Let h·,·i and k·k denote the usual inner product and norm in Rn,respectively.Let f:Rn→R∪{+∞}be a proper convex lower semicontinuous function and F:Rn→2Rnbe a multi-valued mapping.In this paper,we consider the generalized mixed variational inequality problem,denoted by GMVI(F,f,dom(f)),which be defned as
Find x∈dom(f)and ξ∈F(x)such that hξ,y?xi+f(y)?f(x)≥0,?y∈dom(f),(1.1) where dom(f)={x∈Rn:f(x)<+∞}denotes the efective domain of f.Let S be the solution set of problem(1.1).
Problem(1.1)is encountered in many applications,in particular in mechanical problems and equilibrium problems,and hence numerical methods and formulations are studied,see [1–9].On the other hand,the generalized mixed variational inequality problem GMVI(F,f, dom(f))includes a large variety of problems as special instance.For example,let F be the subdiferential of a fnite-valued convex continuous function ψ defned on Rn,the GMVI(F,f,dom(f))becomes the following unconstraint convex optimization problem
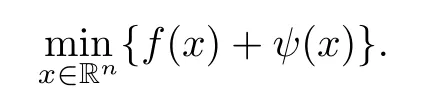
We remark that if F be a single-valued mapping,the problem(1.1)is equivalent to the mixed variational inequality problem
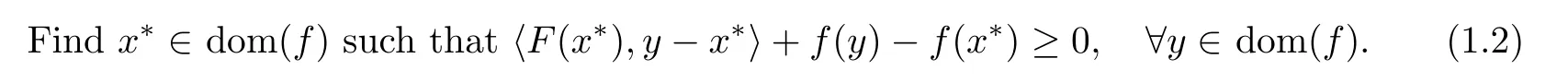
A number of papers in the literature studied the theoretical properties and solution algorithms of problem(1.2),see[10–15].Recently,He[13]extended Algorithm 2.1 of[16]to solve the mixed variational inequality problem.The iteration sequence generated by the algorithm converges to a solution,provided F is f-pseudomonotone and continuous on dom(f),and f is Lipschitz continuous on dom(f).
Furthermore,if f be the indicator function of a nonempty closed convex set K?Rn,that is,
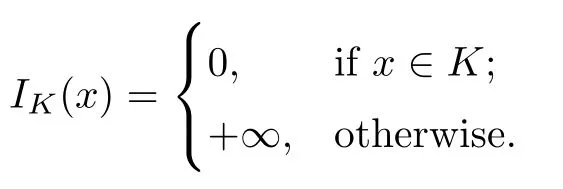
Then problem(1.2)reduces to the variational inequality problem(in short,VI(F,K)):

Many algorithms for solving the VI(F,K)are projection algorithms that employ projections onto the feasible set K of VI(F,K),or onto some related sets,in order to iteratively reach a solution,see[16–20]and the references therein.In particular,Solodov and Svaiter[16]suggested a new projection method,known as the double projection method,for solving problem(1.3).It consists two steps.First,a hyperplane is constructed,which strictly separates current iterate from the solution set.The construction of this hyperplane requires an Armijo-type linesearch. Then the next iterate is produced by projecting the current iterate onto the intersection of the set K and the hyperplane.[18]showed that Solodov and Svaiter’s method obtain a longer stepsize,and guarantee that the distance from the next iterative point to the solution set has a large decrease;and hence it’s a better method than the method proposed by Iusem and Svaiter [19].
On the other hand,if f(x)=IK(x)for all x∈Rn,then problem(1.1)collapses to:

which is called the classical generalized variational inequality problem,denoted by GVI(F,K). Browder[21]introduced problem(1.4)and studied the existence of its solution.Since then, theory and algorithm of GVI(F,K)were much studied in the literatures,see[1,17,21–25]and the references therein.By using diferent Armijo-type linesearches and constructing proftable hyperplanes,which separating strictly current point xiand the solution set S,[24,25]proposed some double projection algorithms for generalized variational inequality problems.For these papers,the separating hyperplane determines the convergence speed of the sequence generated by the double projection algorithm.
Inspired and motivated by the above results,we suggest a new projection-type algorithm to solve the generalized mixed variational inequality problem.In our algorithm,we suggest a newArmijo-type linesearch procedure and construct a suitable separating hyperplane separating strictly current point xiand the solution set S.We also obtain the convergence theorem of our algorithm under some suitable conditions.The algorithm presented in this paper generalize and improve Algorithm 2.1 of Solodov and Svatier(SIAM J.Control Optim.37(3):765-776,1999) or Algorithm 3.1 of He(Acta Math.Sci.27A(2):215-220,2007).Noting that,if f(x)=IK(x) for all x∈Rn,our algorithm is diferent from Algorithm 1 of[24,25].Furthermore,we present some numerical tests(see Example 4.1 and 4.2 below).Example 4.1 shows that our algorithm can be applied to solve problem(1.1);Example 4.2 shows that our algorithm can solve(1.4) (for the case that f(x)=IK(x)for all x∈Rn).Moreover,comparing with Algorithm 1 of [24,25],our method can obtain better numerical results.
2 Preliminaries
In this section,we list some well known concepts and propositions.
Defnition 2.1Let f:Rn→R∪{+∞}be a proper convex function,and K?dom(f) be a nonempty set,f is said to be δ?Lipschitz continuous on K(for some δ>0)if

Defnition 2.2Let f:Rn→R∪{+∞}be a proper convex function,K?dom(f)be a nonempty,closed and convex set,and F:K→2Rnbe a multi-valued mapping.F is said to be
(i)lower semicontinuous at x∈K,if we give any sequence{xk}?K converging to x and any y∈F(x),there exist a sequence yk∈F(xk)such that converges to y.
(ii)upper semicontinuous at x∈K,if for every open set V containing F(x),there is an open set U containing x such that F(y)?V for all y∈K∩U.
(iii)continuous at x∈K,if it is both lower semicontinuous and upper semicontinuous at x.
(iv)pseudomonotone on K,if for any x,y∈K,u∈F(x),v∈F(y),
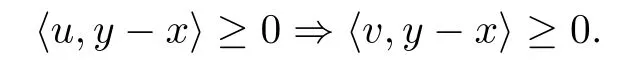
(v)monotone on K,if for any x,y∈K,u∈F(x),v∈F(y),
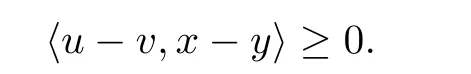
(vi)f-pseudomonotone on K,if for any x,y∈K,u∈F(x),v∈F(y),
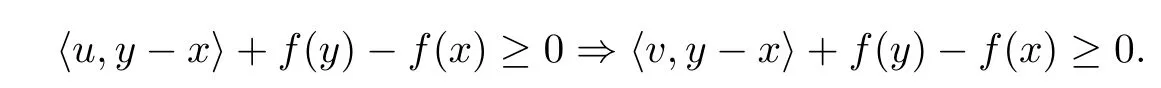
Remark 2.3(i)Obviously,a monotone mapping must be a f-pseudomonotone mapping. A f-pseudomonotone mapping is not necessary monotone,see Example 3.2 below.
(ii)If f≡0,then a f-pseudomonotone mapping reduces to a pseudomonotone mapping.
(iii)We would like to point that the notion of f-pseudomonotonicity was used to study gap functions and global error bounds for generalized mixed variational inequalities in Hilbert spaces by Tan et al.[7],the F-complementarity problems in Banach spaces by Yin et al.[26], and the stability analysis for minty mixed variational inequalities in refexive Banach spaces by Zhong et al.[27].
Notice that the following Defnition 2.4 and Lemma 2.5 are from[10].
Defnition 2.4For any maximal monotone operator A:Rn→Rn,the resolvent operator associated with A of parameter λ be defned as follows:
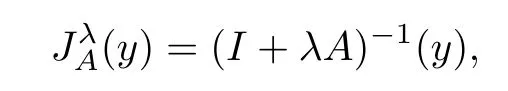
where λ>0 is a constant and I denotes the identity operator.
Let f be a proper convex lower semicontinuous function,the subdiferential of f at x∈dom(f)is the set
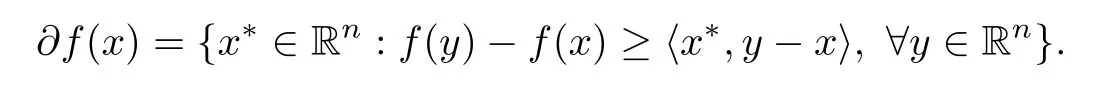
From[10],we know?f is a maximal monotone operator;and hence for each λ>0,Jλf:= (I+λ?f)?1is single-valued and nonexpansive,i.e.,
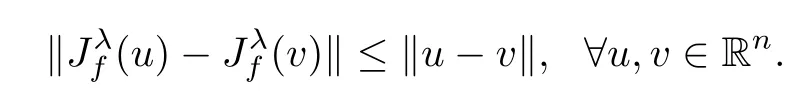
The resolvent operator Jλf(·)has the following useful characterization.
Lemma 2.5For a given v∈Rnand λ>0,the inequality
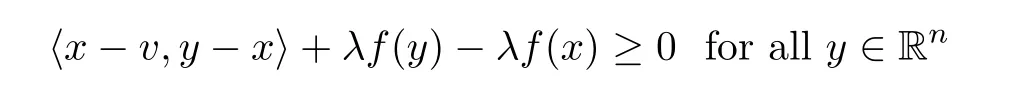
holds if and only if x=Jλf(v).
Notice that if f be the indicator function of a closed convex set K?Rn,then the resolvent operator Jλf(·)reduces to the projection operator PK(·),defned by
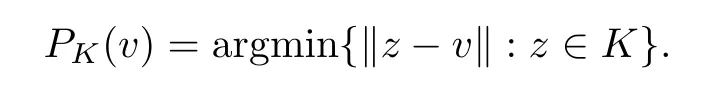
Let dist(x,K)denotes the distance from x to the nonempty subset K,i.e.,
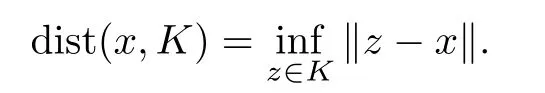
The projection operator PK(·)was extensively studied and we list some properties as follows.See ref.[28]for more details.
Lemma 2.6Let K be a nonempty,closed and convex subset of Rn.Then for any x,y∈Rnand z∈K,
(1)dist(x,K)=kx?PK(x)k;
(2)kPK(x)?zk2≤kx?zk2?kPK(x)?xk2.
For simplifying the notation,for any x∈Rn,ξ∈F(x)and λ>0,we let r(x,λ,ξ):= x?Jλf(x?λξ).The following proposition is simple.
Proposition 2.7If x?∈dom(f)solves GMVI(F,f,dom(f))if and only if there exists ξ?∈F(x?)such that
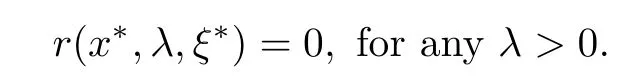
Proposition 2.7 provides us a stopping criterion in designing the algorithm.
3 The Algorithm and Convergence Analysis
In this section,we assume that the resolvent of f can be easy to compute and propose our projection-type algorithm formally.Some related properties are presented.We prove the convergence theorem under the following conditions:
(C1)The solution set S of GMVI(F,f,dom(f))is nonempty.
(C2)f is a proper convex function such that dom(f)is closed.
(C3)f is Lipschitz continuous on dom(f)with modulus β>0.
(C4)F is a continuous and f-pseudomonotone mapping with nonempty compact convex values on dom(f).
Remark 3.1(a)Clearly,assumption(C2)implies that dom(f)is a nonempty,closed and convex subset of Rn.
(b)Let f be the indicator function of a closed convex set K,the above assumptions be used to construct double projection algorithm for generalized variational inequalities,see[24,25].
(c)Let F be single-valued,assumptions(C1)–(C4)be used to construct the algorithm for solving problem(1.2)by[13,15];we also give the following Example 3.2 that satisfes all the conditions when F is multi-valued.
Example 3.2Let n=1,and f be defned by
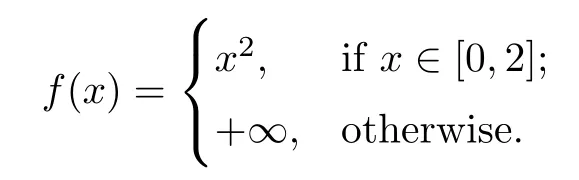
Let F:R→2Rbe defned by
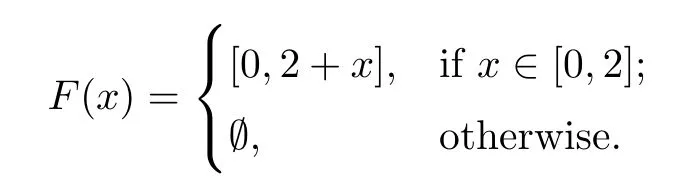
Now we have the following conclusions:
(a)f is a proper convex function,and dom(f)=[0,2].
(b)It is easy to see that x=0 solves GMVI(F,f,dom(f)).
(c)Clearly,f is a 4-Lipschitz continuous mapping on dom(f).
(d)F is f-pseudomonotone on dom(f).In fact,let x,y∈[0,2],u∈F(x)=[0,2+x],v∈F(y)=[0,2+y],if
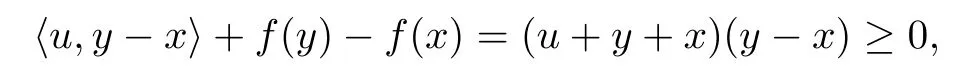
then y≥x and hence
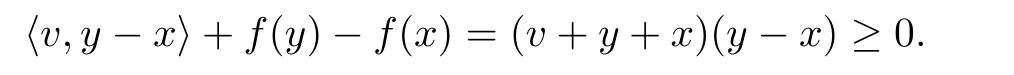
(e)Clearly,F is a continuous mapping with nonempty compact convex values on dom(f).
(f)F is not monotone on dom(f).Let x=1,y=2,u=3∈F(x)and v=2∈F(y),it follows that
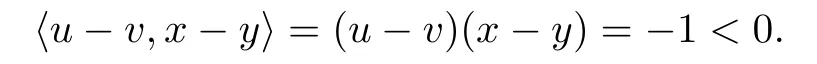
Algorithm 3.3Choose x0∈dom(f)and take two parameters σ∈(0,1),γ∈(0,1).Set i=0.
Step 1Take arbitrarilyξi∈F(xi),compute?xi=J1f(xi?ξi)and r(xi,1,ξi).If r(xi,1,ξi)= 0,stop;else go to Step 2.
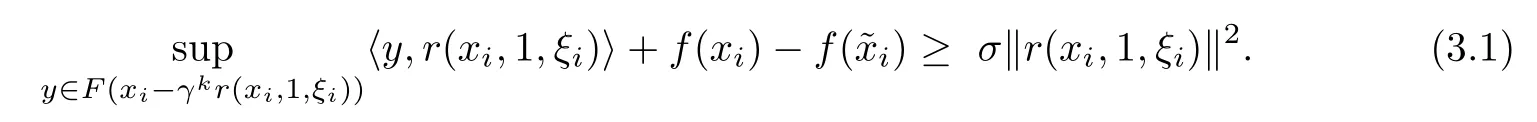
Step 2Let kibe the smallest nonnegative integer satisfyingSet ηi:=γki,zi=xi?ηir(xi,1,ξi)and yi∈argmax{hy,r(xi,1,ξi)i|y∈F(zi)}.
Step 3Compute the next iterate xi+1=PCi(xi),where Ci:={x∈dom(f):hi(x)≤0}, and
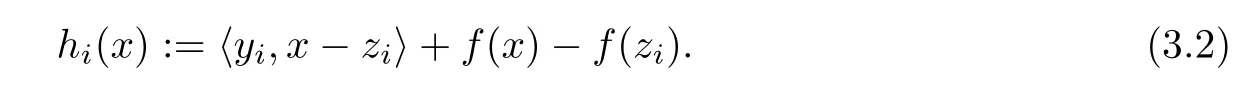
Let i:=i+1 and return to Step 1.
Remark 3.4The computation of yiin Step 2 is implementable in some special cases.In particular,if F(xi?γkr(xi,1,ξ))is a polytope,then it has fnitely many extreme points,i.e.,Thus
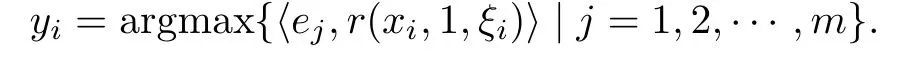
Remark 3.5Algorithm 3.3 includes some algorithms as special case:
(i)Let F be a single-valued mapping and f be the indicator function of a nonempty closed convex set K,then Algorithm 3.3 becomes Algorithm 2.1 in[16].
(ii)Let F be a single-valued mapping,then Algorithm 3.3 becomes Algorithm 3.1 in[13].
Remark 3.6If f be the indicator function of a nonempty closed convex set K,Algorithm 3.3 can be used to solve generalized variational inequality problem.Let us compare the above algorithm with Algorithm 1 in[24,25].
(i)ξican be taken arbitrarily in our method.In[24],choosing ξineeds solving a singlevalued variational inequality and hence is computationally expensive.
(ii)Comparing our algorithm with Algorithm 1 in[24,25],we use diferent Armijo-type linesearch process and hyperplane.
First,we show that Algorithm 3.3 is well defned,and hence our algorithm is implementable, provided the resolvent of f is easy to compute exactly.Obviously,if r(xi,1,ξi)=0 for some i≥0,then it terminates at a solution of problem GVMI(f,F,dom(f)).Therefore,from now on,we assume that r(xi,1,ξi)6=0 for all i≥0.
Lemma 3.7If r(xi,1,ξi)6=0,then there exists a nonnegative integer kisatisfying(3.1).
ProofSuppose(3.1)is not satisfed for any integer k,that is,
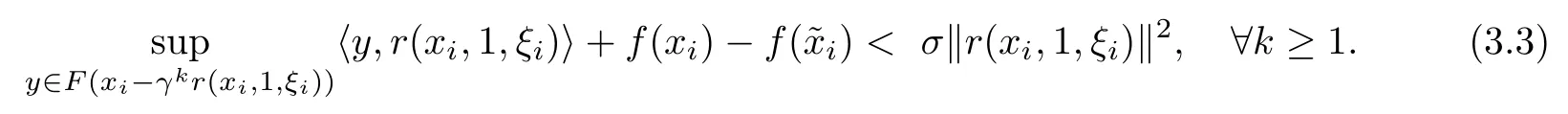
Applying Lemma 2.5 with λ:=1,v:=xi?ξi,x:=?xiand y:=xi,we get
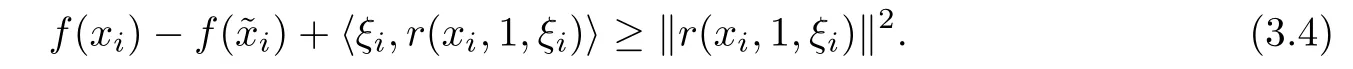
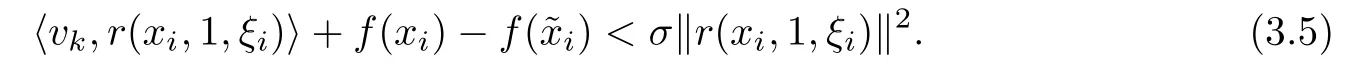
Let k→∞in(3.5),we get that
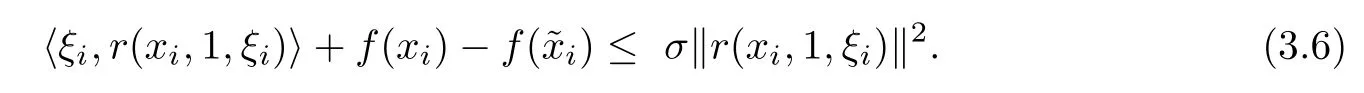
Combining(3.4)and(3.6),we have σ≥1.This is a contradiction,which completes the proof.
Now,we list some useful lemmas as follows.
Lemma 3.8(see[13]) Let h:Rn→R be a real-valued function on Rn.Let K be the set{x∈Rn:h(x)≤0}such that K?D?dom(f).If h is Lipschitz continuous on D with modulus θ>0,then
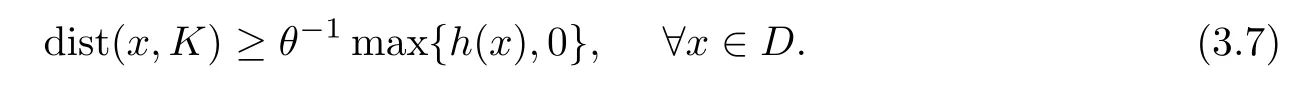
Lemma 3.9Let x?solves GMVI(F,f,dom(f))and the function hibe defned by(3.2). Then hi(xi)≥ηiσkr(xi,1,ξi)k2and hi(x?)≤0.In particular,if r(xi,1,ξi)6=0,then hi(xi)>0.
ProofIt follows directly from the defnition of hi(x)that
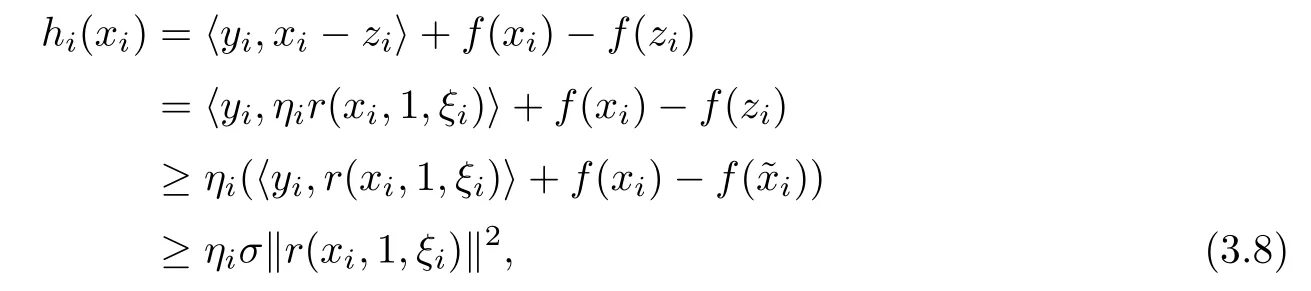
where the frst inequality is from the convexity of f,the last one is from inequality(3.1).If r(xi,1,ξi)6=0,it follows from(3.8)that hi(xi)>0.
We next prove that hi(x?)≤0.Since x?∈S,there exist ξ?∈F(x?)such that
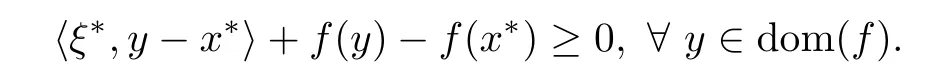
Taking y:=ziin the above inequality,we obtain that
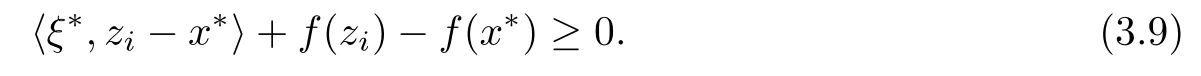
By the f-pseudomonotonicity of F,it follows from yi∈F(zi)that
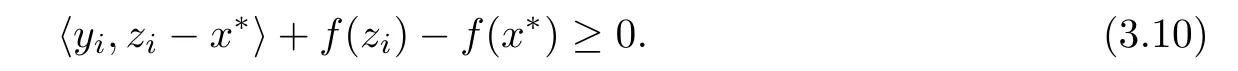
That is hi(x?)≤0,which completes the proof and implies x?∈Ci.
Theorem 3.10Suppose that Assumptions(C1)–(C4)hold.Then either Algorithm 3.3 terminates in a fnite number of iterations or generates an infnite sequence{xi}converging to a solution of problem(1.1).
ProofLet x?∈S.We assume that Algorithm 3.3 generates an infnite sequence{xi}. Thus,for each i,r(xi,1,ξi)6=0.It follows that
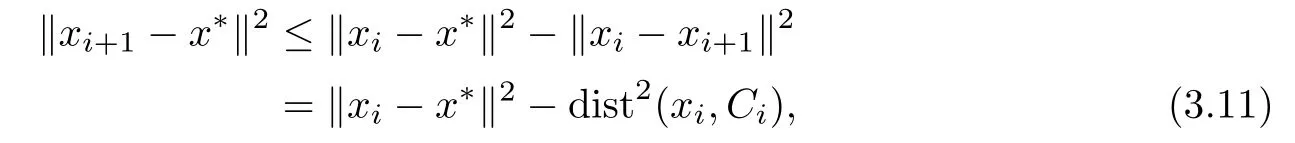
where the inequality follows from x?∈Ciand Lemma 2.6(2),the equality follows from Lemma 2.6(1).It follows from(3.11)that{kxi?x?k}is a convergent sequence,i.e.,there exists some δ≥0 such that

Therefore,{xi}is bounded and

Since F is continuous with compact convex values,Proposition 3.11 of[29]implies that{F(xi): i∈N}is a bounded set,and so the sequence{ξi}is bounded.Since J1f(·)is nonexpansive,we have that
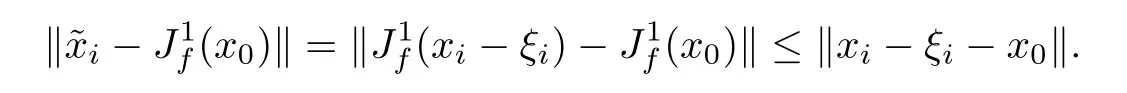
By the above inequality,we obtain that there exist M>0,
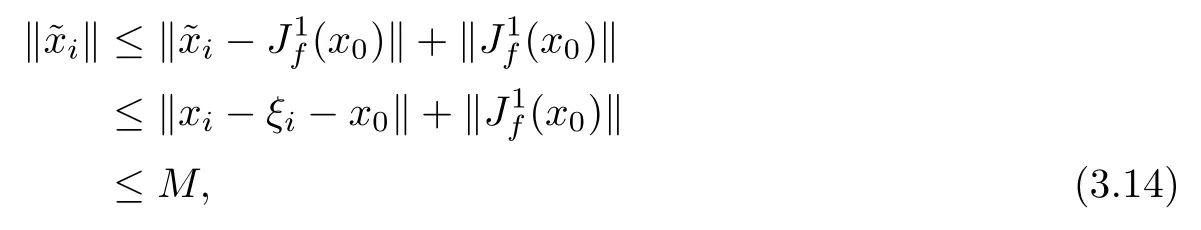
and hence the sequences{?xi},{r(xi,1,ξi)}are bounded.Since zi=xi?ηir(xi,1,ξi),we have that the sequence{zi}is bounded.Similar,we obtain that the sequence{yi}is bounded.Thus there exist τ≥0 such that kyik≤τ.Thus,hiis Lipschitz continuous on dom(f)with modulus (τ+β)>0.Noting that xi/∈Ci,and applying Lemma 3.8,we have
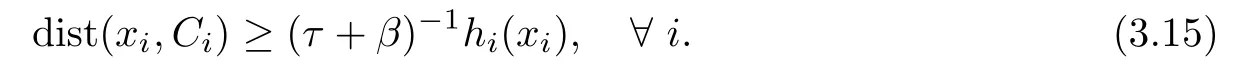
It follows from Lemma 3.9 and(3.15)that
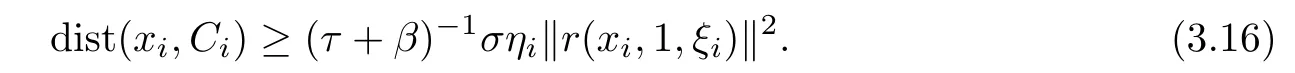
By(3.13)and(3.16),it follows that

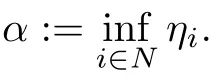
If α>0,it follows from(3.17)that
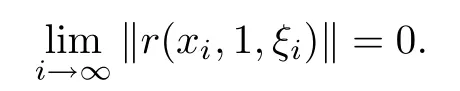
Since r(·,1,·)is continuous and the sequence{xi}and{ξi}are bounded,there exists an accumulation point(ˉx,ˉξ)of{(xi,ξi)}such that r(ˉx,1,ˉξ)=0.Since F is upper semicontinuous with compact convex values,Proposition 3.7 of[29]implies that F is closed and soˉξ∈F(ˉx). That is,ˉx∈dom(f)is a solution of GMVI(F,f,dom(f)).
Suppose now that α=0.Let(ˉx,ˉξ)be an accumulation point of{(xi,ξi)}.Thus,there exists an index set I such that
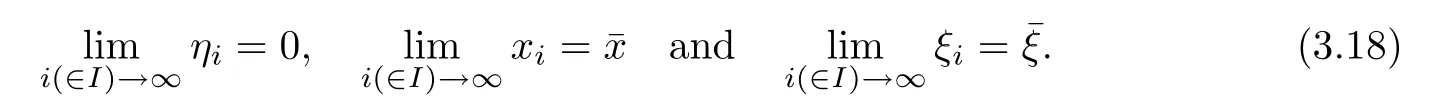
It follows that
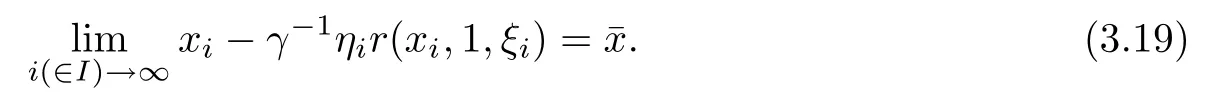
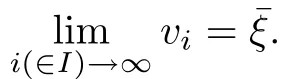
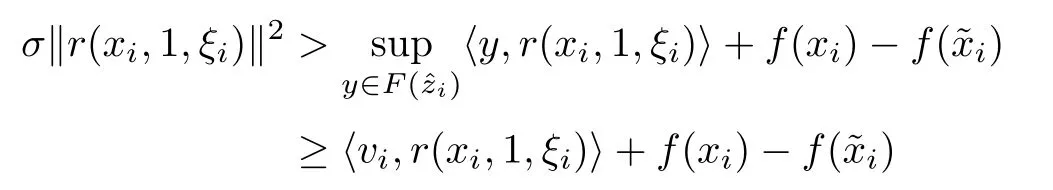
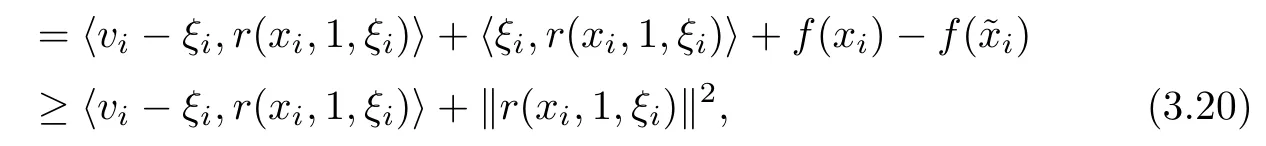
where the frst inequality is from the construction of ki,the second inequality is from vi∈F(?zi), the last one is from(3.4).Letting i∈I and i→∞in(3.20),we obtain r(ˉx,1,ˉξ)=0.The above two cases prove that there exists an accumulation pointˉx of the sequence{xi}such that ˉx∈dom(f),
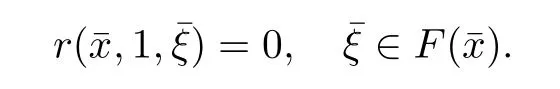
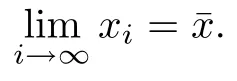
4 Numerical Experiments
In this section,we present some numerical experiments for the proposed method.The MATLAB codes are run on a PC(with Intel(R)Core(TM)i7-5500U CPU@2.4GHz(4CPUs), 8192MB RAM)under MATLAB Version 7.12.0.635(R2011a)Service Pack 1 which contains optimization Toolbox version 6.0.
In Example 4.1,we use our algorithm to compute the solution point of problem(1.1).The computational experiments show that our algorithm is valid and efective.
In Example 4.2,we use our algorithm to compute the solution of problem(1.4).If n=4, the GVI(F,K)which we use in Example 4.2 is used in[25].Thus,Example 4.2 is a extension of the one in[25].The computational experiment shows that our algorithm is efective to solve GVI(F,K).Moreover,comparing with Algorithm 1 in[24,25],our method can obtain better numerical results.
In Table 1,Table 2 and Table 3,“Iter.”denotes number of iteration and“CPU”denotes the CPU time seconds.We use“nf.”for the total number of times that F is evaluated.The tolerance ? means when kr(x,1,ξ)k≤?,the procedure stops.
Example 4.1Let n=4,
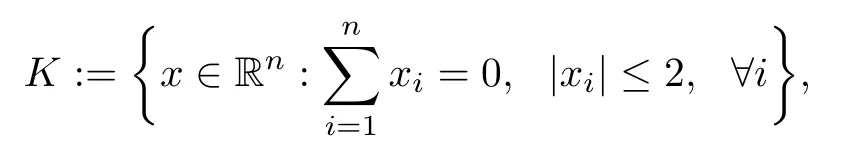
and f be defned by
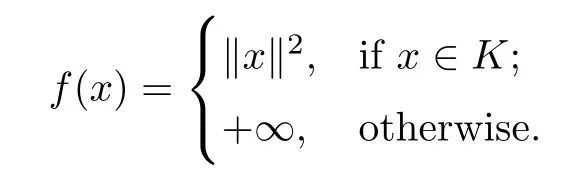
Let F:Rn→2Rnbe defned by
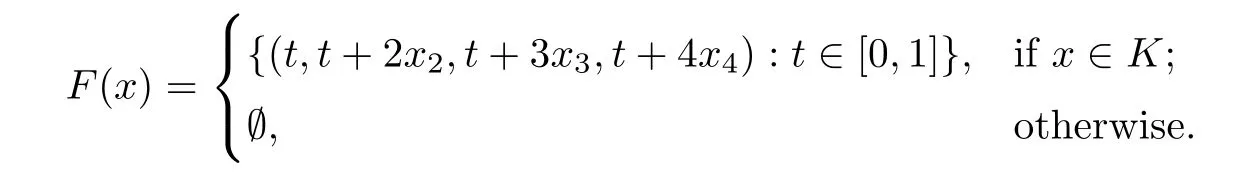
It is easy to know that all the assumptions in Theorem 3.10 are satisfed and x=(0,0,0,0) is a solution of GMVI(F,f,dom(f)).
Now we show that the resolvent of f can be computed.For any g∈Rn,let z=(I+?f)?1(g).It follows that fnding z is equivalent to solving the following separable convex programming

where θj(xj)=x2j+12(xj?gj)2,K0={v∈R:|v|≤2}.Problem(4.1)can be considered as a special case of multi-block convex minimization problems:

It follows that fnding z is equivalent to solving the VI(F,K)with F(x)=3x?g.Since F is strongly monotone with modulus 3 and K is a nonempty compact convex set,it follows that the above variational inequality has a unique solution z.Thus,the solution point z can be computed by some known algorithms for classical variational inequality problem.We use Algorithm 2.1 of Slodov and Svaiter in[16]to compute the solution point z in this example and choose σ=0.5,γ=0.9 for our Algorithm 3.3 in Table 1.

Table 1 Result for Example 4.1
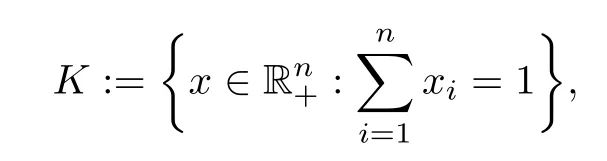
Example 4.2Letand F:K→2Rnbe defned by
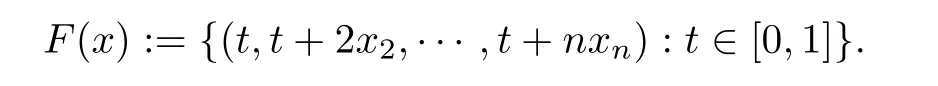
Let f(x)=IK(x),it is easy to know that all the assumptions in Theorem 3.10 are satisfed and(1,0,···,0)is a solution of GVI(F,K).Notice that if n=4,the GVI(F,K)which we use in Example 4.2 is used in[25].Thus,Example 4.2 is a extension of the one in[25].We frst let n=4(n denotes the dimension of Euclidean space)(see Table 2),and then we let n=8 (see Table 3).The choice of parameters of example 4.2 for Algorithm 1 of[24,25]is what the reference[25]proposed.We choose σ=0.3 and γ=0.7 for our Algorithm 3.3 in Table 2 and Table 3.
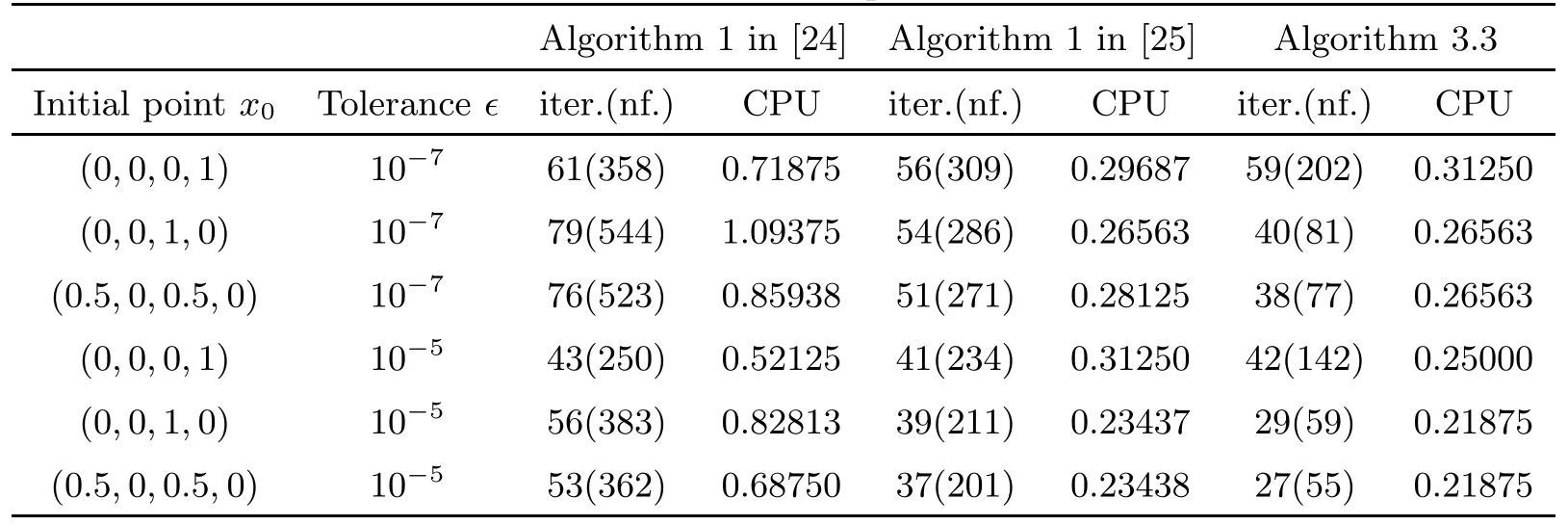
Table 2 Result for Example 4.2 with n=4
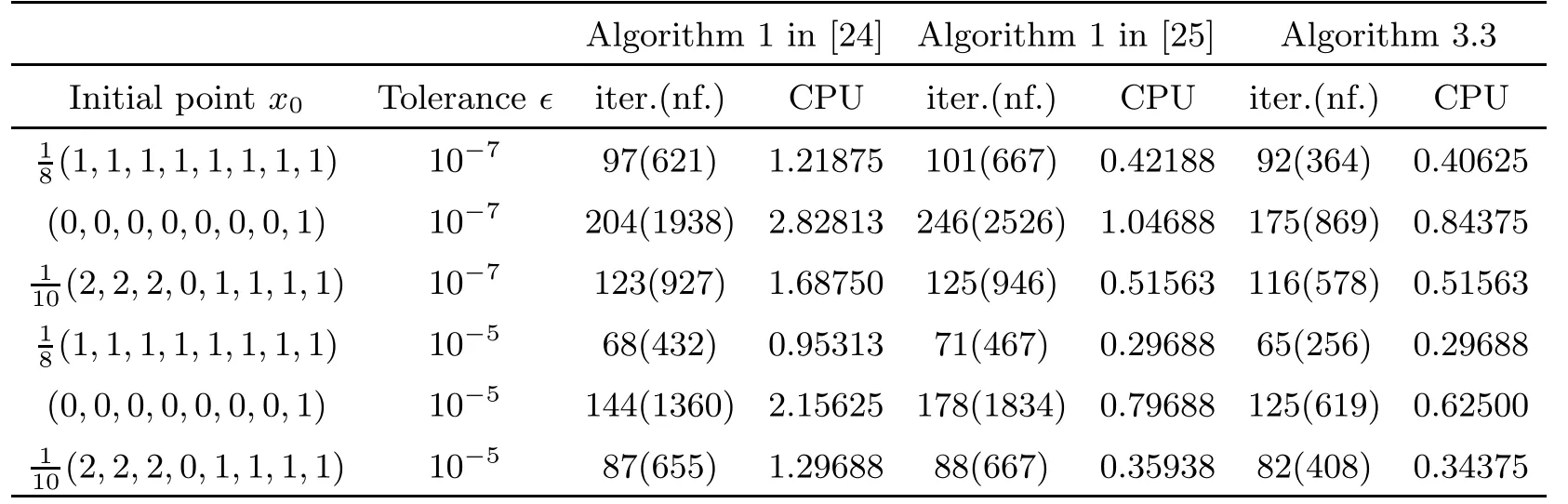
Table 3 Result for Example 4.2 with n=8
[1]Rockafellar R T.Monotone operators and the proximal point algorithm.SIAM J Control Optim,1976, 14(5):877–898
[2]Tseng P.Applications of a splitting algorithm to decomposition in convex programming and variational inequalities.SIAM J Control Optim,1991,29(1):119–138
[3]Han W M,Reddy B D.On the fnite element method for mixed variational inequalities arising in elastoplasticity.SAIM J Numerical Anal,1995,32(6):1778–1807
[4]Chinchuluun A,Pardalos P M,Migdalas A,et al.Pareto Optimality,Game Theory and Equilibria.Berlin: Springer,2008
[5]Xia F Q,Huang N J,Liu Z B.A projected subgradient method for solving generalized mixed variational inequalities.Oper Res Lett,2008,36(5):637–642
[6]Wu K Q,Huang N J.The generalized f-projection operator and set-valued variational inequalities in Banach spaces.Nonlinear Anal:TMA,2009,71(7):2481–2490
[7]Tang G J,Huang N J.Gap functions and global error bounds for set-valued mixed variational inequalities. Taiwan J Math,2013,17(4):1267–1286
[8]Tran D Q,Muu L D,Nguyen V H.Extragradient algorithm extended to equilibrium problems.Optim, 2008,57(6):749–779
[9]Dinh B V,Muu L D.A projection algorithm for solving pseudomonotone equilibrium problems and its application to a class of bilevel equilibria.Optim,2013,64(3):559–575
[10]Brezis H.Operateurs Maximaux Monotone et Semi-Groupes de Contractions Dans Les Espaces de Hilbert. Amsterdam:North-Holland Publishing Company,1973
[11]Bnouhachem A.A self-adaptive method for solving general mixed variational inequalities.J Math Anal Appl,2005,309(1):136–150
[12]Zeng L C,Yao J C.Convergence analysis of a modifed inexact implict method for general monotone variational inequalities.Math Methods Oper Res,2005,62(2):211–224
[13]He Y R.A new projection algorithm for mixed variational inequalities.Acta Math Sci,2007,27A(2): 215–220
[14]Xia F Q,Li T,Zou Y Z.A projection subgradient method for solving optimization with variational inequality constraints.Optim Lett,2014,8(1):279–292
[15]Tang G J,Zhu M,Liu H W.A new extragradient-type method for mixed variational inequalities.Oper Res Lett,2015,43(6):567–562
[16]Solodov M V,Svaiter B F.A new projection method for variational inequality problems.SIAM J Control Optim,1999,37(3):765–776
[17]Facchinei F,Pang J S.Finite-dimensional Variational Inequalities and Complementarity Problems.New York:Springer-Verlag,2003
[18]Wang Y J,Xiu N H,Wang C Y.Unifed framework of extragradient-type methods for pseudomonotone variational inequalities.J Optim Theory Appl,2001,111(3):641–656
[19]Iusem A N,Svaiter B F.A variant of Korpelevich’s method for variational inequalities with a new search strategy.Optim,1997,42(4):309–321
[20]He Y R.A new double projection algorithm for variational inequalities.J Comput Appl Math,2006,185(1): 166–173
[21]Browder F E.Multi-valued monotone nonlinear mapping and duality mappings in Banach space.Trans Amer Math Soc,1965,118:338–351
[22]Anh P N,Muu L D,Nguyen V H,Strodiot J J.Using the Banach contraction principle to implement the proximal point method for multivalued monotone variational inequalities.J Optim Theory Appl,2005, 124(2):285–306
[23]Xia F Q,Huang N J.A projection-proximal point algorithm for solving generalized variational inequalities. J Optim Theory Appl,2011,150(1):98–117
[24]Li F L,He Y R.An algorithm for generalized variational inequality with pseudomonotone mapping.J Comput Appl Math,2009,228(1):212–218
[25]Fang C J,He Y R.A double projection algorithm for multi-valued variational inequslities and a unifed framework of the method.Appl Math Comput,2011,217(23):9543–9551
[26]Yin H Y,Xu C X,Zhang Z X.The F-complementarity problems and its equivalence with the least element problem.Acta Math Sinica,2001,44(4):679–686
[27]Zhong R Y,Huang N J.Stability analysis for minty mixed variational inequality in refexive Banach spaces. J Optim Theory Appl,2010,147(3):454–472
[28]Polyak B T.Introduction to Optimization.New York:Optimization Software,1987
[29]Aubin J P,Ekeland I.Applied Nonlinear Analysis.New York:John Wiley&Sons Incorporated,1984
[30]Lin T Y,Ma S Q,Zhang S Z.On the global linear convergence of the ADMM with multi-block variables. SIAM J Optim,2015,25(3):1478–1497
?Received July 16,2015;revised March 22,2016.This work was supported by the Scientifc Research Foundation of Sichuan Normal University(20151602),National Natural Science Foundation of China(10671135, 61179033),and the Key Project of Chinese Ministry of Education(212147).
?Corresponding author:Kai TU.
 Acta Mathematica Scientia(English Series)2016年6期
Acta Mathematica Scientia(English Series)2016年6期
- Acta Mathematica Scientia(English Series)的其它文章
- NEW LOWER BOUNDS FOR LEE DISCREPANCY ON TWO AND THREE MIXED LEVELS FACTORIALS?
- THREE SOLUTIONS FOR A FRACTIONAL ELLIPTIC PROBLEMS WITH CRITICAL AND SUPERCRITICAL GROWTH?
- SHARP ESTIMATES OF ALL HOMOGENEOUS EXPANSIONS FOR A SUBCLASS OF QUASI-CONVEX MAPPINGS OF TYPE B AND ORDER α IN SEVERAL COMPLEX VARIABLES?
- MULTIPLICITY RESULTS FOR A NONLINEAR ELLIPTIC PROBLEM INVOLVING THE FRACTIONAL LAPLACIAN?
- EXISTENCE AND UNIQUENESS OF NON-TRIVIAL SOLUTION OF PARABOLIC p-LAPLACIAN-LIKE DIFFERENTIAL EQUATION WITH MIXED BOUNDARIES?
- PROPERTIES OF THE MODIFIED ROPER-SUFFRIDGE EXTENSION OPERATORS ON REINHARDT DOMAINS?
