The performance of proper orthogonaldecomposition in discontinuous flows
Jing Li,Weiwei ZhangSchoolofAeronautics,Northwestern PolytechnicalUniversity,Xi'an 710072,China
Letter
The performance of proper orthogonaldecomposition in discontinuous flows
Jing Li,Weiwei Zhang?
SchoolofAeronautics,Northwestern PolytechnicalUniversity,Xi'an 710072,China
H I G H L I G H T S
.The proper orthogonaldecomposition(POD)modes have specialpattern for flow existing shock wave.
.The reason why reconstructing transonic flow needs more POD modes is explained.
.POD combined with interpolation has good prediction ability for transonic flow.
.POD combined with extrapolation does not have prediction ability for transonic flow.
A R T I C L E I N F O
Article history:
Received 4 June 2016
Received in revised form
4 July 2016
Accepted 7 August 2016
Available online 24 August 2016
POD Interpolation Shock wave Transonic flow Prediction
In this paper,flow reconstruction accuracy and flow prediction capability of discontinuous transonic flow field by means of proper orthogonal decomposition(POD)method is studied.Although linear superposition of''high frequency waves''in different POD modes can achieve the reconstruction of the shock wave,the smoothness of the solution near the shock wave cannot be guaranteed.The modal coefficients are interpolated or extrapolated and different modal components are superposed to realize the prediction of the flow field beyond the snapshot sets.Results show that compared with the subsonic flow,the transonic flow with shock wave requires more PODmodes to reach a comparative reconstruction accuracy.When a shock wave exists,the interpolation prediction ability is acceptable.However,large errors exist in extrapolation,and increasing the number of POD modes cannot effectively improve the prediction accuracy ofthe flow field.
?2016 The Authors.Published by Elsevier Ltd on behalfof The Chinese Society of Theoreticaland Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).
The proper orthogonal decomposition(POD),also known as Karhunen-Loeve(K-L)expansion or principle components analysis,has been widely used in many areas,such as image processing[1],pattern recognition[2],reduced order model[3](ROM), flow dynamics analysis[4,5],and airfoil design optimization[6], and so on.POD method is a powerfulstatisticaltoolwhich can extract the significant structure or pattern from a large data set.POD method is also an effective reduction toolwhich can use the minimum number of POD modes to present a large data ensemble with the given accuracy.Lumley[7]firstly introduced the POD method into the turbulent flow.Then,Sirovich[8]introduced snapshots as a way to efficiently determine the POD modes,which made POD method applied to a wider range of problems,especially to computationalfluid dynamics(CFD).
Numerical simulation of fluid flows is a very computationally intensive endeavor.In addition,reaching a physicalunderstanding from numerical simulation data is another challenge.Faced with these two challenges,ROM is a good choice that retains the essential physics and dynamics of the fluid flows,but has a much lower computational cost.This can enable uncertainty quantification[9],on-the-spot decision-making[10],optimization[11], and control[12].There are two approaches in constructing an efficient ROMbased on PODby integrating with Galerkin method[13-16]or surrogate technique[17,18].One approach is based on Galerkin projection of the physicalmodelon a reduced-dimension basis determined by POD.Xie et al.[19]employed this scheme to solve the nonlinear aeroelastic oscillations of a fluttering plate in both two and three dimensions.Pla et al.[20]described a flexible Galerkin method based on POD to construct the bifurcation diagram.Furthermore,Kim[21]developed the ROMin frequency form using a set of discrete snapshots in frequency domain instead of time domain.However,the POD-Galerkin ROM is non-robust and structurally unstable[22].Therefore,some new approaches are developed to improve the stability and reliability of the POD-Galerkin ROM.Xiao et al.[23]applied a new non-linear Petrov-Galerkin method to the reduced order Navier-Stokesequations,thus improving the stability of ROM.Romain et al.[24] investigated sequential data assimilation techniques to improve the stability of POD-Galerkin ROM for fluid flows.Leblond and Allery[25]obtained a priori low-dimensional space-time separated representation ofthe fluid fields,which is based on the use of space-time proper generalized decomposition(PGD)definitions. PGD may be seen as a generalization of the POD for a priori construction of a separated representation ofthe solution.This allows ensuring the accuracy ofa ROMas the parameter varies.The other approach to construct the POD-based ROMis to utilize a surrogate modelas a function ofthe measurement POD coefficients.Mainini and Willcox[10]combined POD and a localpolynomial response surface model to realize a fast mapping from measured quantities to system capabilities.This assists online rapid decision making for an unmanned aerialvehicle.Fossati[26]integrated PODand multidimensional interpolation for the parametric evaluation of steady aerodynamic loads.Kato and Funazaki[27]combined POD and radial basis function network(RBFN)for adaptively sampling a design parameter space using an error estimate through the reconstruction offlow field.
However,because of shock waves,boundary-layer separation, and control-surface deflection in the transonic flow regime,additional complexities of the nonlinear aerodynamic system may be introduced.Especially,shock waves involve jumps in the flow variables,which bring great difficulties in POD-based ROM[28-30]. This results in either a quite poor approximation between ROM and CFD or a huge number of POD modes[31,32].And some special treatments are needed to avoid that problem.Iuliano and Quagliarella[11]presented a zonal approach to better solve the shock wave region and improve the ROM prediction in transonic flow.Malouin et al.[33]proposed an idea thatis to use POD to interpolate the difference between the CFDsolution obtained on two different grids,a coarse one and a fine one.This allows some nonlinearities associated with the flow to be introduced and gets good improvement over the classical approach.Taeibi-Rahni et al.[34] proposed the filtered and reprojection POD for transonic flow and better results were obtained than the conventional POD method. Butthere are no explanations why POD method results in poor approximation when dealing with shock waves and needs more POD modes to improve the behavior.Thus,this paper conducts research on this question.The performances of POD method for flow reconstruction in both subsonic and transonic flows are tested.Results show that different from subsonic flow,there are''high frequency waves''in the POD modes oftransonic flow.This is the reason why reconstructing shock waves with satisfactory accuracy needs more POD modes.Furthermore,this will result in the prediction failure of the flow field beyond snapshot sets.
POD can be applied efficiently to large systems using the method of snapshots[6]as followsis a collection of m flow snapshots,where Ukis a vector containing the flow solution ata time or a parameter,such as the angle ofattack(AOA)or Mach number.And usually these solutions are expressed as the sum of average values and fluctuation values.

The correlation matrix R is formed by computing the inner product between every pair of snapshots,

where denotes the inner product betweenAnd then compute the eigenvaluesand eigenvectorsThe orthonormalPODmodes can be obtained by the following formula:
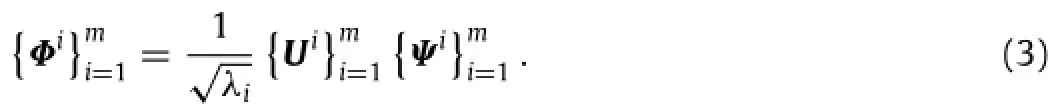
The magnitude of the i th eigenvalue,λi,describes the relative importance of the i th POD mode,also known as the relative energy contained in the i th POD mode.
The approximate reconstruction of the flow solutions can be given by the sum ofaverage values and a linear combination of the POD modes:

where p?m and p is chosen to capture the desired levelofenergy.is the modal coefficient,corresponding to the i th POD mode, which can be obtained by projecting the k th snapshot to the i th POD mode.
POD method combined with interpolation and extrapolation can realize the fast prediction of flow solutions which are not contained in the snapshots[26].The main steps are as follows:
(2)Perform the basic POD procedure described above to get the truncated orthonormal POD modesand the corresponding POD coefficients

In this paper,the steady flow solutions to a NACA 0012 airfoilwith varying AOA are used as snapshots.CFD solver adopts advection upstreamsplitting method(AUSM)+UP scheme to solve the Euler equation.Unstructured grid is used.The number ofnodes is 6916 and the number of cells is 13490,as shown in Fig.1. A detailed description of the solver and its verification can be referred to in Ref.[35].
The snapshots set of case 1 is composed of 100 flow solutions ensemble at the fixed Mach number of 0.8,with AOA range of [0.25°,2.23°],uniformly spaced with an interval of 0.02°.Among them,two shock waves are separately located on the upper surface and the lower surface of the airfoilin the first 70 snapshots,while there is only one shock wave on the upper surface in the last 30 snapshots.With the increase ofAOA,the position ofthe shock wave gradually moves downstream.And the range of the shock wave on the upper surface corresponding to the x-axis is 0.53-0.71.Figure 2 shows the distribution ofpressure coefficients on the upper surface at different AOAs,which illustrates the position change of the shock wave with the AOA rang.Based on this snapshots set, reconstruction of the flow solution is conducted by the POD method.For a distinct demonstration,POD method is applied only to the pressure field and the pressure is dimensionless.The procedure of the other flow fields is straightforward.
In order to better illustrate the impact of shock waves on the reconstruction result of the flow field based on POD method,a subsonic case 2 is tested.The snapshots set of case 2 is composed ofa steady flow solution ensemble atthe fixed Mach number of0.5 and the AOArange,spacing and the number ofsnapshots are allthe same as in case 1.
Figure 3 shows the first to the third PODmodes ofthe above two cases.As can be seen from Fig.3(d)to(f),the contour of the upper airfoilsurface displays a ribbon pattern.And the value distribution of these ribbons alternates in a positive and negative way.Wecall these ribbons''high frequency waves'',the maximum value of which corresponds to the peak and the minimum value of which corresponds to the valley.The''frequency''in''high frequency wave''has no correlation with time.It expresses the reciprocal of wavelength.In subsonic case,the POD modes change smoothly. And so is the region except where the shock wave appeared and moved at POD modes of transonic case.If these smooth changes are considered as part of a wave,the wavelength of these waves is much longer than that at shock wave appeared and moved region. Therefore,the dense changes at shock wave appeared and moved region are called''high frequency wave''.Furthermore,the number of''half waves''is correlated with the order of POD modes.And in case 1,the number of''half waves''is equal to the order of POD mode.The range of''high frequency waves''is roughly the same as the moving range of the shock wave in the snapshots set.With the increasing order of POD mode,the wavelength of''high frequency waves''decreases gradually and the amplitude increases gradually. Only the shock wave on the upper surface willbe discussed and the contour of the lower airfoil surface has the similar regularity.The linear superposition of these''high frequency waves''reproduces the shock wave of the flow field.However,under the premise of the reconstruction accuracy ofthe shock wave,the''high frequency waves''at different amplitudes and frequencies in other regions can hardly offset each other.Therefore,oscillation phenomenon occurs before and after the shock wave.With the increase of POD modes used in reconstruction,the oscillation frequency increases while the oscillation amplitude decreases gradually.Furthermore, the range of oscillation is roughly the same as that of''high frequency waves''in POD modes,as shown in Figs.4 and 5. To better illustrate the oscillation phenomenon in reconstruction flows,surface pressure coefficients are presented here.Figures 4 and 5 show the comparison of the surface pressure coefficient between the POD and the CFD.Figures 6 and 7 compare the flow field reconstructed by POD method with that computed by CFD solver.Figures 4 and 6 present the first snapshot flow.Figures 5 and 7 present the one hundredth snapshot flow.Other snapshots have the same regularities.
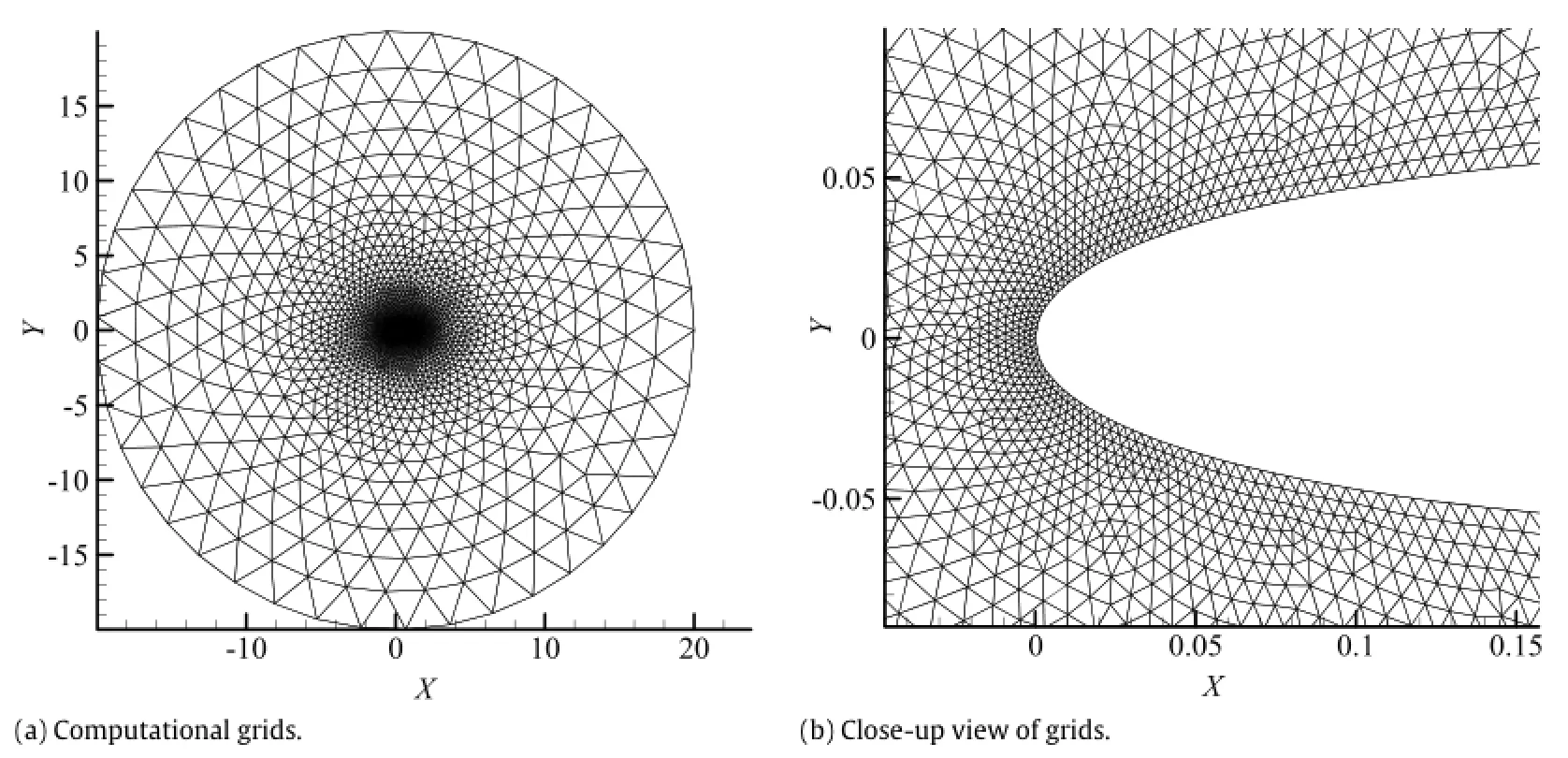
Fig.1.Computationalgrids.
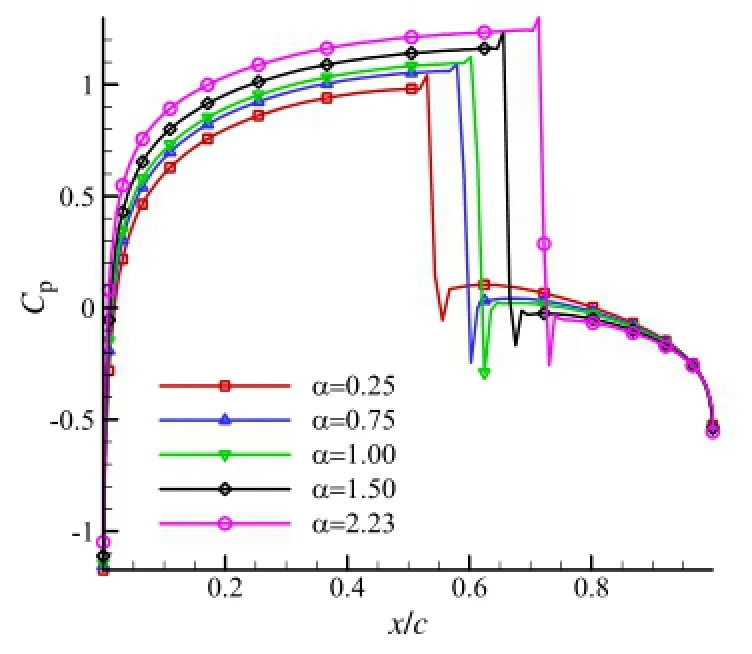
Fig.2.Pressure coefficient distribution of airfoilwith AOAs range.

Table 1 The order of POD mode needed to achieve specified energy.
Figure 8 shows the eigenvalue curves of the two cases.It can be seen that the eigenvalue of M=0.8 declines slowly and the phenomenon of''most energy contained in the first few PODmodes''is notobvious.As shown in Table 1,at M=0.5,it only needs one POD mode to achieve 99%or 99.9%ofthe totalenergy;while at M=0.8, it requires 9 POD modes to achieve 99%of the totalenergy and 21 POD modes to achieve 99.9%of the total energy.Therefore,if the energy is regarded as a standard of POD mode truncation,the flow with shock waves requires more POD modes to reach the specified energy.Taking the 71th snapshot as an example,Fig.9 shows the comparison of surface pressure coefficient obtained by POD and CFD in the two cases.Figure 9(a)shows thatin the state of the transonic speed with shock waves(M=0.8),even if the POD modes which are needed to reach 99.9%of the totalenergy are used,oscillation phenomenon stilloccurs before and after the shock wave. Butoutside this region,even ifone PODmode is used,surface pressure coefficients obtained by POD agree well with those by CFD. However,in the state of the subsonic speed(M=0.5),with only one POD mode,pressure coefficients atthe whole surface obtained by PODagree wellwith those by CFD,as shown in Fig.9(b).This difference is mainly caused by the shock discontinuity in snapshots.
In order to quantify the deviation between the reconstructed flow field and the actual flow field,the reconstruction error is defined as follows:
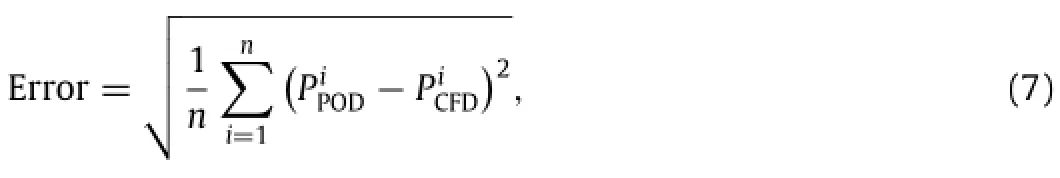
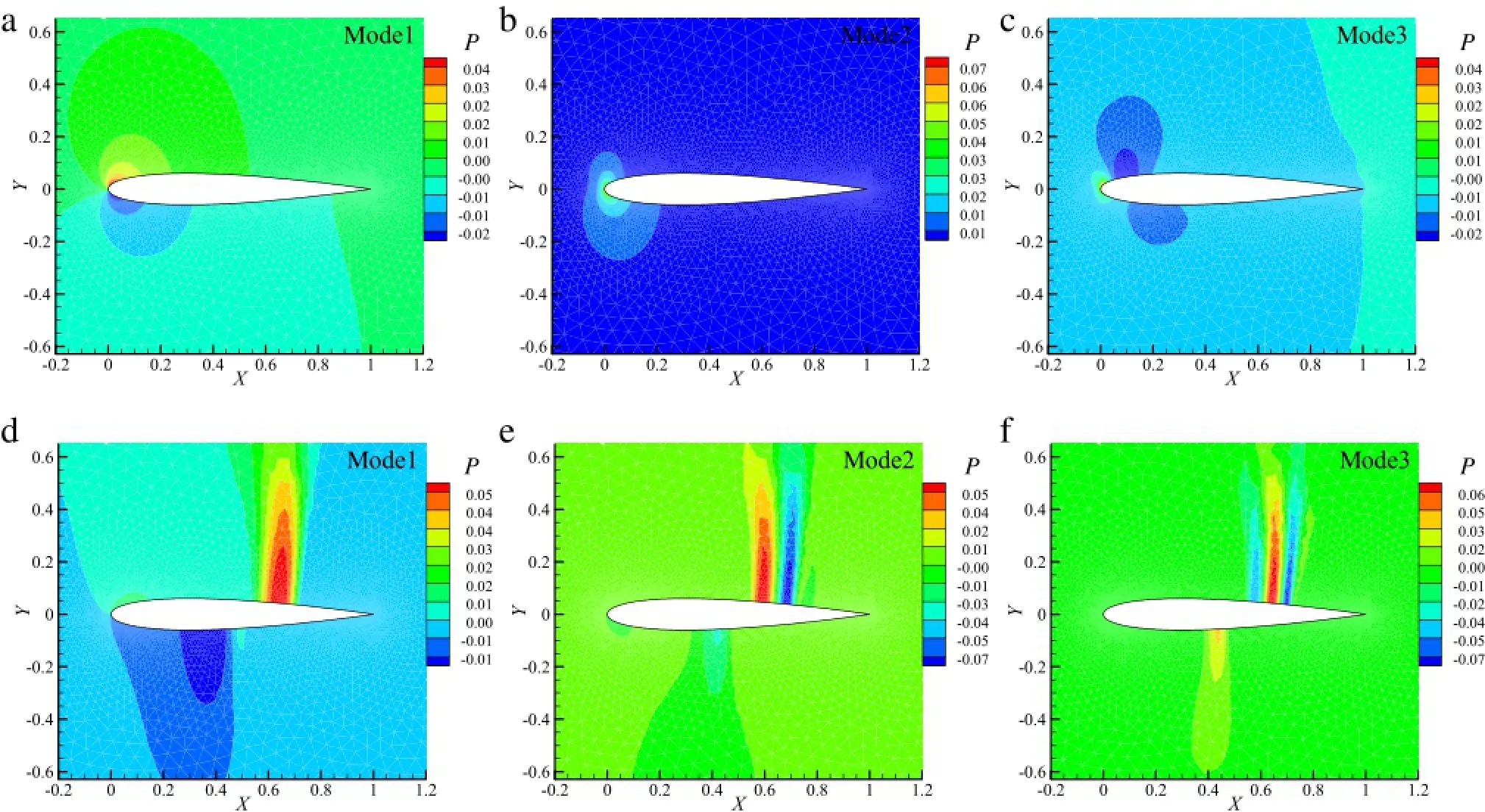
Fig.3.(Color online)POD modes(case2:(a)-(c);case1:(d)-(f)).
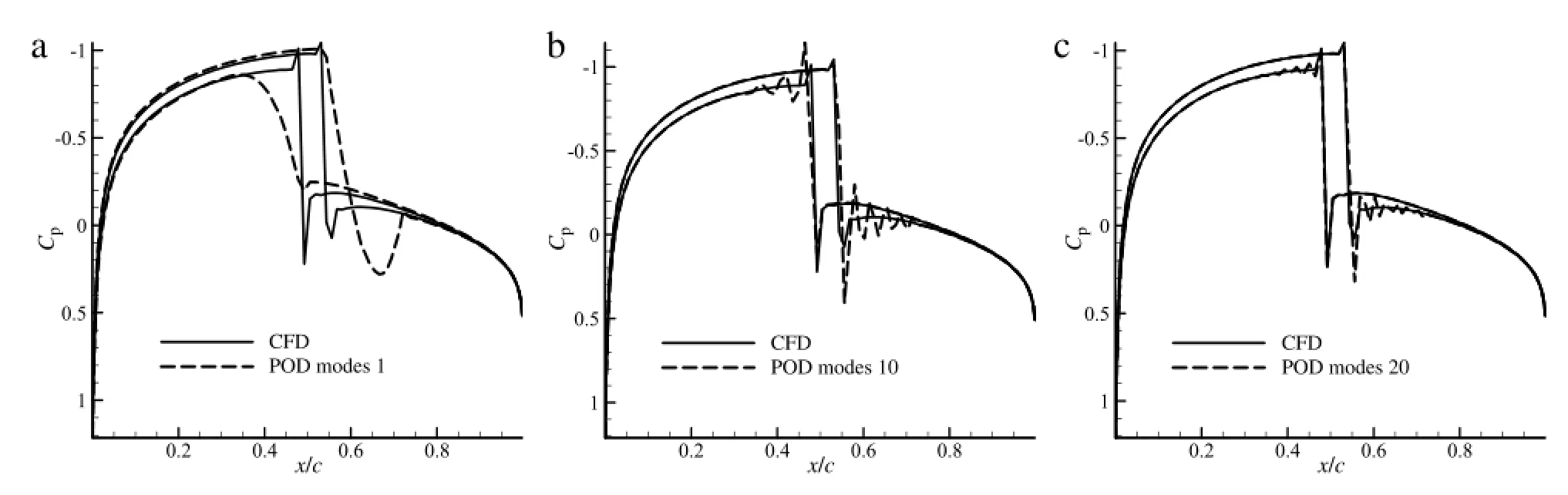
Fig.4.Comparison ofthe surface pressure coefficient between the POD and the CFD at snapshot 1(α=0.25°).
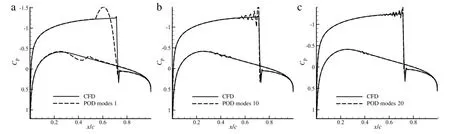
Fig.5.Comparison ofthe surface pressure coefficient between the POD and the CFD at snapshot 100(α=2.23°).
We also take case 1 and case 2 described above as comparison. POD coefficients are interpolated or extrapolated according to theabove interpolation steps,so as to realize the prediction of flow field solutions which are not contained in the snapshots set.The flow field ofα=1.84°is taken as the presentation example in interpolation and the flow field ofα =2.26°in extrapolation. Figure 11 shows the modalcoefficients comparison between real value and interpolation result of the two cases.The real value is obtained by Eq.(5).The AOArange of[0.25°,2.23°]is resulted from interpolation and the AOA range of[2.24°,2.25°]is resulted from extrapolation.
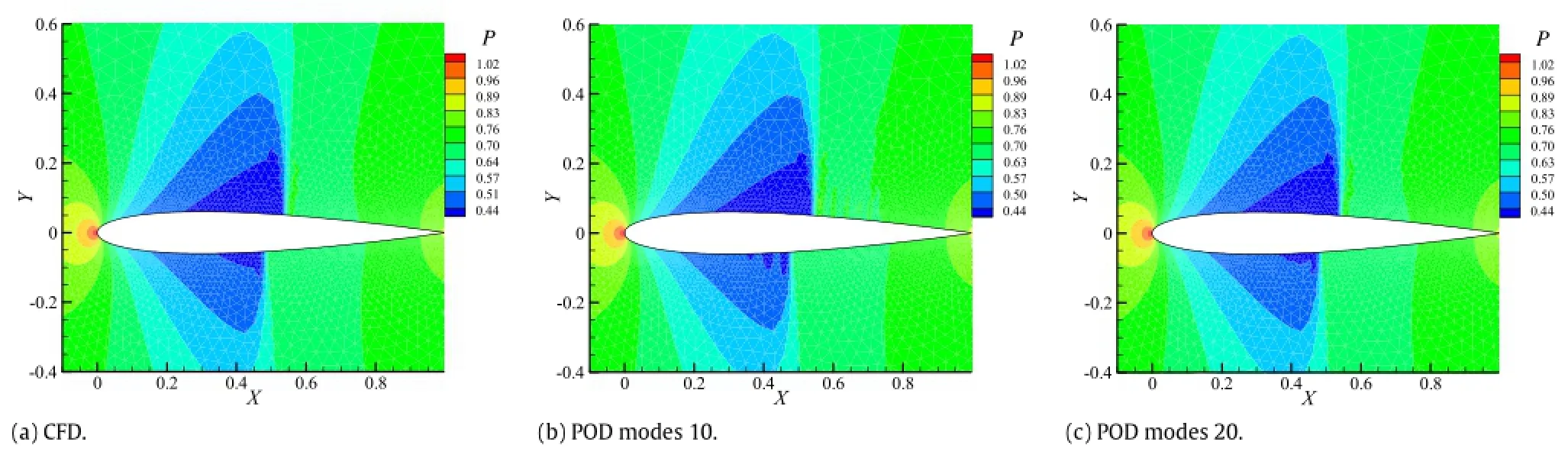
Fig.6.(Color online)Comparison ofthe flow field between the POD and the CFD at snapshot 1(α=0.25°).
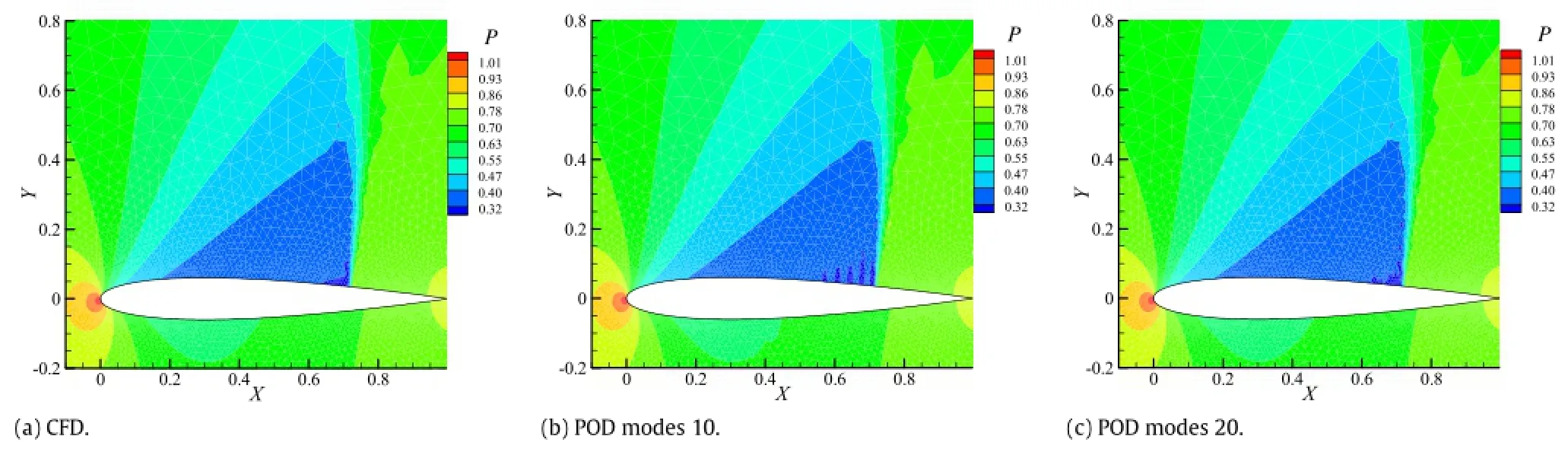
Fig.7.(Color online)Comparison of the flow field between the POD and the CFD at snapshot 100(α=2.23°).
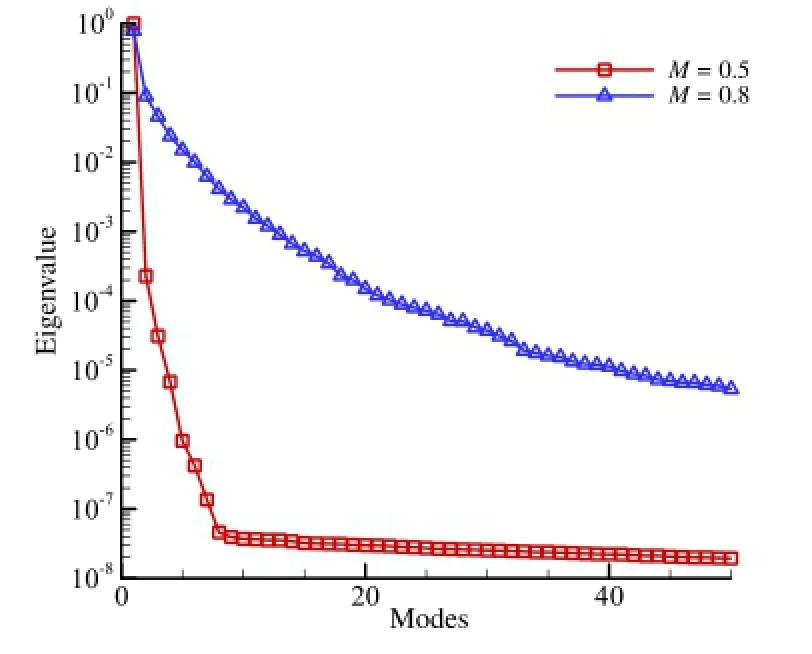
Fig.8.Eigenvalue curve.
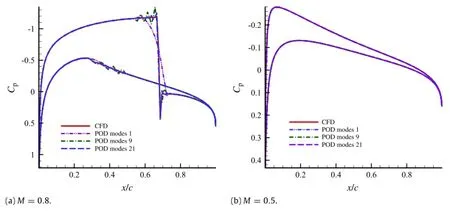
Fig.9.Comparison ofthe surface pressure coefficient between the POD and the CFD at snapshot 71(α=1.65°).
For flow with the shock discontinuity,POD method combined with interpolation has relatively good prediction ability.But the shock discontinuity in the flow also causes the increase of the prediction error in POD method combined with interpolation. The analysis results are similar to that of the reconstruction. The surface pressure coefficient curve of POD interpolation at M =0.8 still shows oscillation phenomenon before and afterthe shock wave while other regions agree very well with that of CFD,as shown in Fig.12.Furthermore,with the increase of POD modes,the oscillation frequency increases gradually and the amplitude decreases gradually.And with enough POD modes,it can achieve higher reconstruction accuracy.Figure 13 shows the interpolation error curve with the POD modes.It can be seen that the interpolation error curves of the two cases are all convergent with the POD modes.However,the interpolation error at M=0.8 is 2-3 orders of magnitude higher than that at M=0.5.
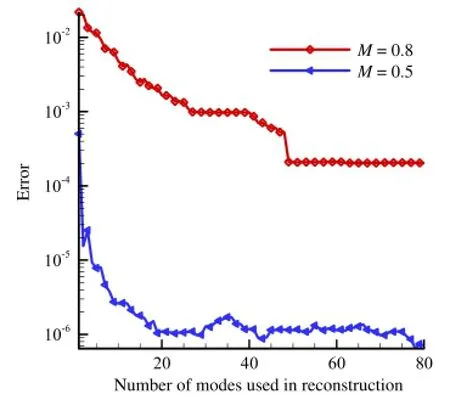
Fig.10.Reconstruction error curve(snapshot71,α=1.65°).
Figure 14 shows the comparison of surface pressure coefficient between POD extrapolation and CFD.It can be seen that oscillation phenomenon still occurs at M = 0.8.But if POD modes are increased,the oscillation amplitude cannot be decreased.It also can be seen from Fig.15 that the prediction curve with POD modes is notconvergent.When POD modes used in the prediction are increased,the prediction error increases instead of decrease. However,the extrapolation prediction error curve at M =0.5 converges quickly and maintains at a low value.Therefore,the shock discontinuity in the flow destroys the prediction ability of POD method combined with extrapolation so that it no longer has the extrapolation ability.

Fig.13.Prediction error curve of POD interpolation.
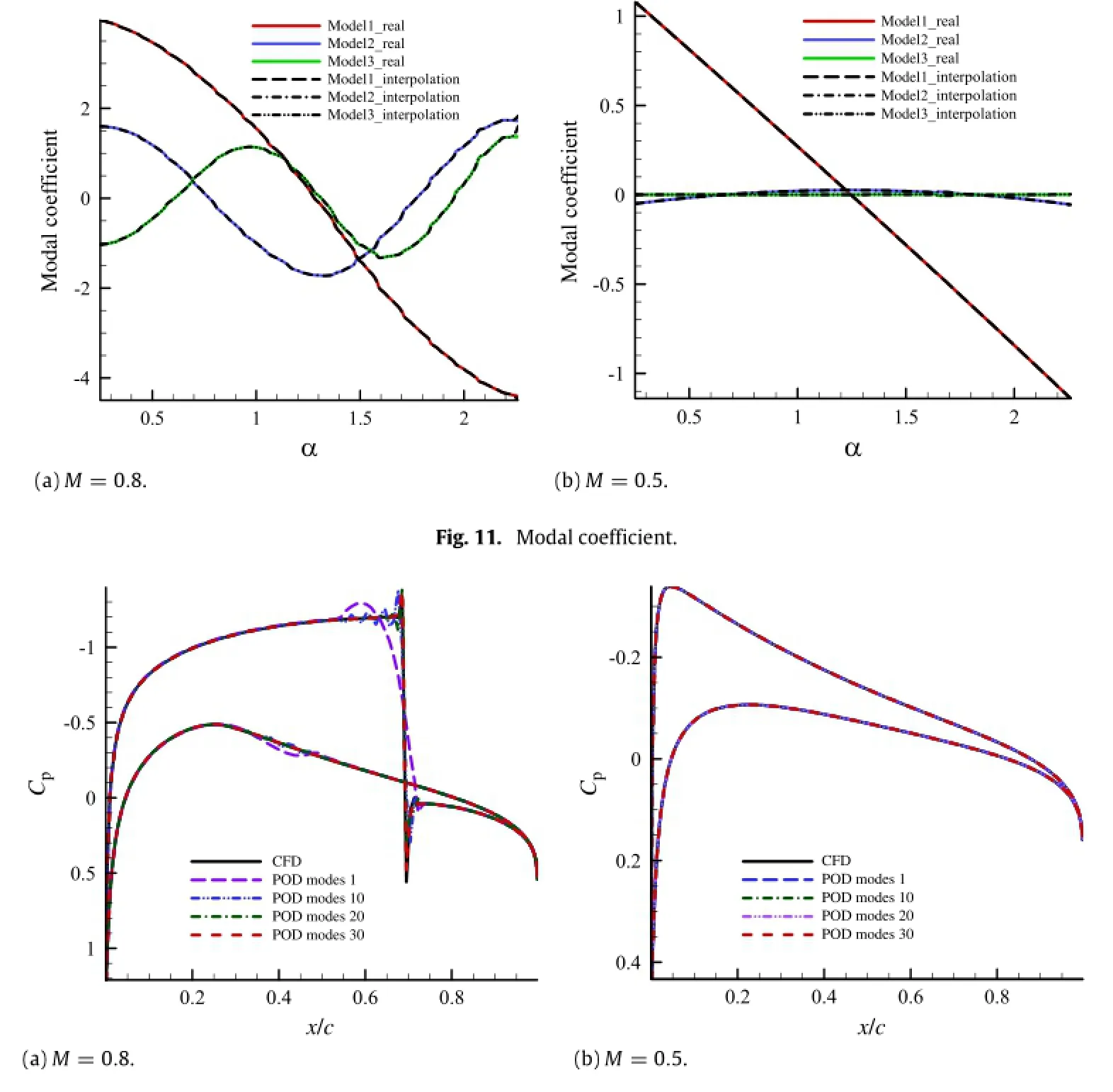
Fig.12.Surface pressure coefficient of POD interpolation and CFD.
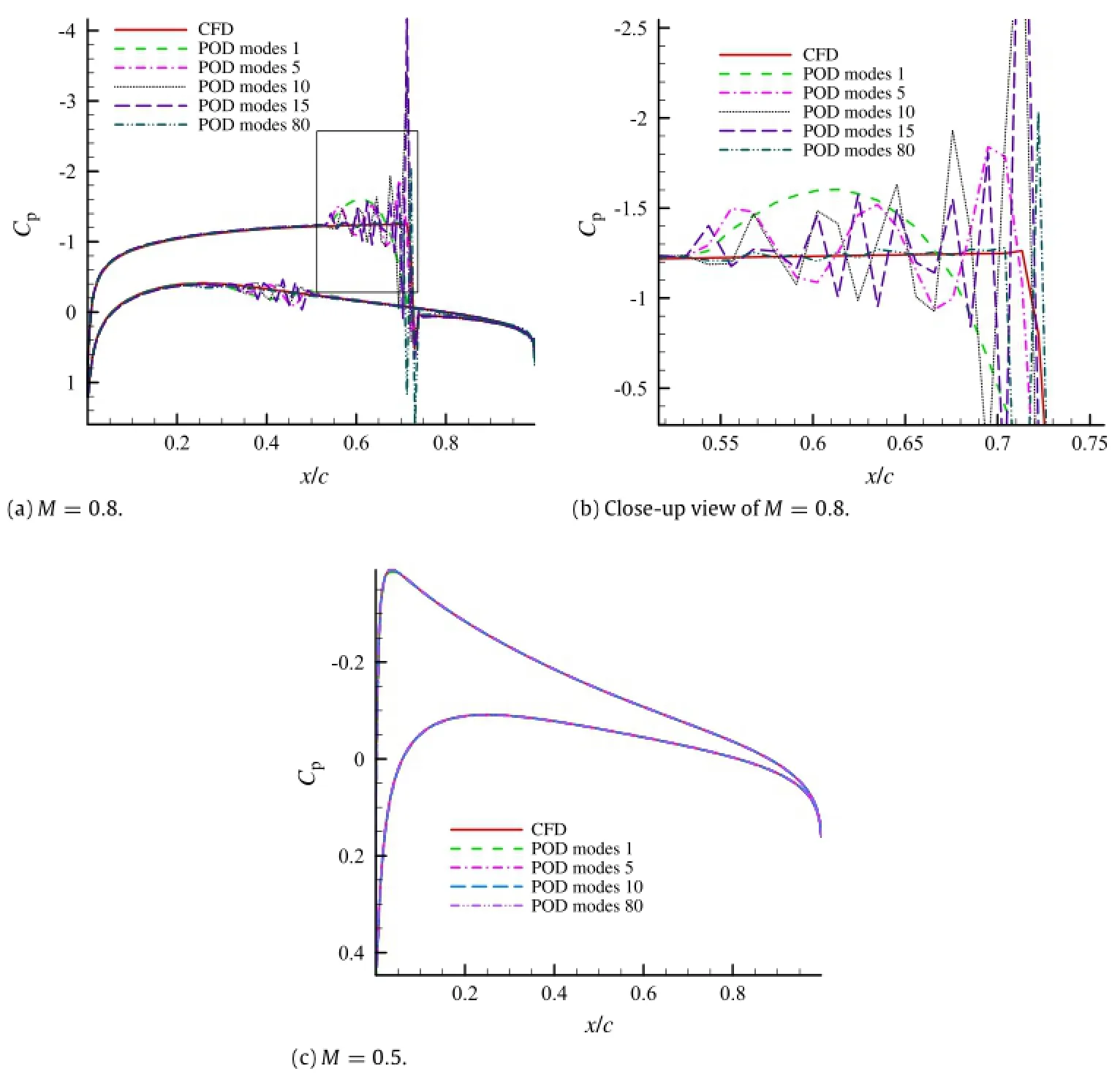
Fig.14.Surface pressure coefficient of POD extrapolation and CFD.
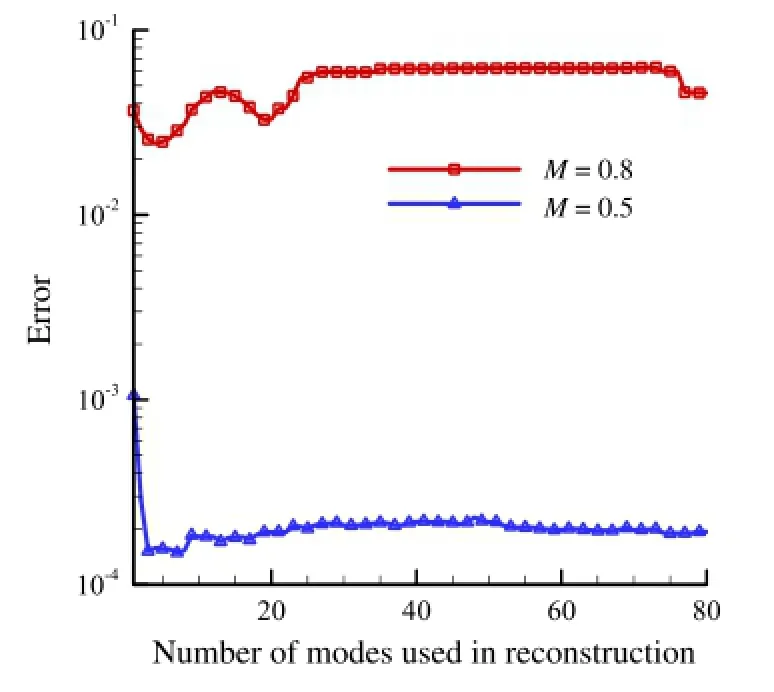
Fig.15.Prediction error curve of POD extrapolation.
For the flow with the shock discontinuity,POD method is used to get POD modes.And then the snapshot is projected to each POD mode to obtain the modal coefficient,so as to realize the reconstruction of flow field.The cubic spline interpolation is conducted on modal coefficients for interpolation or extrapolation to predict flow solution beyond the snapshots set.The reconstruction accuracy and prediction ability of the POD method are studied in the view ofthe discontinuous flow field and following conclusions can be drawn:
(1)The shock discontinuity in snapshots causes the occurrence of''high frequency waves''in POD modes.And the range of''high frequency waves''is roughly the same as the moving range of the shock waves in the snapshots set.With the increasing order of POD mode,the wavelength of''high frequency waves''decreases gradually and the amplitude increases gradually.
(2)The linear superposition of''high frequency waves''in different POD modes can achieve the reconstruction of the shock wave in the flow field.However,under the premise of the reconstruction accuracy of the shock wave,the''high frequency waves''at different amplitudes and frequencies in other regions often hardly offset each other.Therefore,oscillation phenomena appear near the shock waves.Increasing the PODmodes used in the reconstruction can decrease the amplitude ofoscillation Therefore, reconstructing the discontinuity flow field with higher accuracy needs more POD modes.
(3)POD method combined with interpolation or extrapolation is a good way to predict flow solutions for snapshots without the shock discontinuity.However,for snapshots with the shock discontinuity,although this method stillhas a relatively good interpolation prediction ability,the performance of extrapolation is poor.
Acknowledgment
This study was supported by the''National Natural Science Foundation-Outstanding Youth Foundation''.
[1]L.Sirovich,M.Kirby,Low-dimensional procedure for the characterization of human faces,J.Opt.Soc.Amer.A 33(1987)591-596.
[2]K.Fukunaga,Introduction to Statistical Pattern Recognition,Academic Press, 2013.
[3]P.Holmes,J.L.Lumley,G.Berkooz,Turbulence,Coherent Structures,Dynamical Systems and Symmetry,Cambridge University Press,1998.
[4]L.Q.Ma,L.H.Feng,Experimentalinvestigation on controlof vortex shedding mode of a circular cylinder using synthetic jets placed at stagnation points, Sci.China TechnolSc.56(2013)158-170.
[5]W.J.Qin,M.Z.Xie,M.Jia,et al.,Large eddy simulation and proper orthogonal decomposition analysis ofturbulent flows in a direct injection spark ignition engine:Cyclic variation and effect ofvalve lift,Sci.China TechnolSc.57(2014) 489-504.
[6]P.A.LeGresley,J.J.Alonso,Investigation ofnon-linear projection for pod based reduced order models for aerodynamics,AIAA Paper 14(2001)2002-0317.
[7]J.Lumley,The structures of inhomogeneous turbulent flow,in:A.M.Yaglom, V.I.Tatarski(Eds.),Atmospheric Turbulence and Radio Wave Propagation, Nauka,Moscow,1967,pp.166-178.
[8]L.Sirovich,Turbulence and the dynamics of coherent structures.Part I: Coherentstructures,Q.Appl.Math.45(1987)561-571.
[9]O.Roderick,M.Anitescu,Y.Peet,Proper orthogonal decompositions in multifidelity uncertainty quantification ofcomplex simulation models,Int.J. Comput.Math.91(2014)748-769.
[10]L.Mainini,K.Willcox,Surrogate modeling approach to support real-time structuralassessmentand decision making,AIAA J.53(2015)1612-1626.
[11]E.Iuliano,D.Quagliarella,Proper orthogonal decomposition,surrogate modelling and evolutionary optimization in aerodynamic design,Comput. Fluids 84(2013)327-350.
[12]G.Chen,X.Wang,Y.M.Li,Areduced-order-model-based multiple-in multipleout gust alleviation control law design method in transonic flow,Sci.China TechnolSc.57(2014)368-378.
[13]E.H.Dowell,K.C.Hall,J.P.Thomas,et al.,Reduced order models in unsteady aerodynamics,AIAA Paper(1999)99-1261.
[14]N.Z.Cao,N.Aubry,Numericalsimulation ofa wake flow via a reduced system, ASME-Publications-FED 149(1993)53-53.
[15]M.Romanowski,Reduced order unsteady aerodynamic and aeroelastic models using Karhunen-Loeveeigenmodes,in:6th Symposium on Multidisciplinary Analysis and Optimization,1996,p.3981.
[16]D.J.Lucia,P.S.Beran,W.A.Silva,Reduced-order modeling:new approaches for computationalphysics,Prog.Aerosp.Sci.40(2004)51-117.
[17]P.Mokhasi,D.Rempfer,S.Kandala,Predictive flow-field estimation,Physica D 238(2009)290-308.
[18]C.Yang,X.Y.Liu,Z.G.Wu,Unsteady aerodynamic modeling based on POD-observer method,Sci.China TechnolSc.53(2010)2032-2037.
[19]D.Xie,M.Xu,E.H.Dowell,Proper orthogonal decomposition reduced-order modelfor nonlinear aeroelastic oscillations,AIAA J.52(2014)229-241.
[20]F.Pla,H.Herrero,J.M.Vega,A flexible symmetry-preserving Galerkin/POD reduced order model applied to a convective instability problem,Comput. Fluids 119(2015)162-175.
[21]T.Kim,Frequency-domain Karhunen-Loeve method and its application to linear dynamic systems,AIAA J.36(1998)2117-2123.
[22]B.R.Noack,K.Afanasiev,M.Morzynski,et al.,A hierarchy of low-dimensional models for the transient and post-transient cylinder wake,J.Fluid Mech.497 (2003)335-363.
[23]D.Xiao,F.Fang,J.Du,et al.,Non-linear Petrov-Galerkin methods for reduced order modeling ofthe Navier-Stokes equations using a mixed finite element pair.,Comput.Methods Appl.Math.255(2013)147-157.
[24]L.Romain,L.Chatellier,L.David,Bayesian inference applied to spatio-temporal reconstruction of flows around a NACA0012 airfoil,Exp.Fluids 55(2014) 1-19.
[25]C.Leblond,C.Allery,A priori space-time separated representation for the reduced order modeling of low Reynolds number flows,Comput.Methods Appl.Math.274(2014)264-288.
[26]M.Fossati,Evaluation of aerodynamic loads via reduced-order methodology, AIAA J.53(2015)2389-2405.
[27]H.Kato,K.Funazaki,POD-driven adaptive sampling for efficient surrogate modeling and its application to supersonic turbine optimization,in:ASME Turbo Expo 2014:Turbine Technical Conference and Exposition,American Society of MechanicalEngineers,2014,V02BT45A023-V02BT45A023.
[28]Y.Qiu,J.Q.Bai,Stationary flow fields prediction of variable physical domain based on proper orthogonal decomposition and kriging surrogate model, Chinese J.Aeronaut.28(2015)44-56.
[29]R.Huang,H.Li,H.Hu,et al.,Open/Closed-Loop aeroservoelastic predictions via nonlinear,reduced-order aerodynamic models,AIAA J.53(2015)1812-1824.
[30]B.A.Freno,T.A.Brenner,P.G.A.Cizmas,Using proper orthogonal decomposition to model off-reference flow conditions,Int.J.Non-Linear Mech.54(2013) 76-84.
[31]K.Willcox,Unsteady flow sensing and estimation via the gappy proper orthogonaldecomposition,Comput.Fluids 35(2006)208-226.
[32]A.Qamar,S.Sanghi,Steady supersonic flow-field predictions using proper orthogonaldecomposition technique,Comput.Fluids 38(2009)1218-1231.
[33]B.Malouin,J.Y.Trépanier,M.Gariépy,Interpolation of transonic flows using a proper orthogonaldecomposition method,Int.J.Aerosp.Eng.2013(2013) 928904.
[34]M.Taeibi-Rahni,F.Sabetghadam,M.K.Moayyedi,Low-dimensional proper orthogonaldecomposition modeling as a fast approach of aerodynamic data estimation,J.Aerosp.Eng.23(2009)44-54.
[35]Y.Jiang,Numerical Solution of Navier-Stokes Equations on Generalized Mesh and its Applications[Ph.D.Thesis],Northwestern Polytechnical University, Xi'an,2013.
?Corresponding author.
E-mail address:aeroelastic@nwpu.edu.cn(W.Zhang).
http://dx.doi.org/10.1016/j.taml.2016.08.008
2095-0349/?2016 The Authors.Published by Elsevier Ltd on behalfof The Chinese Society of Theoreticaland Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
 Theoretical & Applied Mechanics Letters2016年5期
Theoretical & Applied Mechanics Letters2016年5期
- Theoretical & Applied Mechanics Letters的其它文章
- A modified airfoil-based piezoaeroelastic energy harvester with double plunge degrees of freedom
- A new algorithm ofglobaltightly-coupled transient heat transfer based on quasi-steady flow to the conjugate heat transfer problem
- Side force controlon slender body by self-excited oscillation flag
- The Richtmyer-Meshkov instability of a'V'shaped air/helium interface subjected to a weak shock
- High temperature effects in moving shock reflection with protruding Mach stem
- Numericalinvestigation of unsteady mixing mechanism in plate film cooling
