V.H.Carneiro·H.Puga·J.Meireles

?

Analysis of the geometrical dependence of auxetic behavior in reentrant structures by finit elements

V.H.Carneiro1·H.Puga1·J.Meireles1

?The Chinese Society of Theoretical and Applied Mechanics;Institute of Mechanics,Chinese Academy of Sciences and Springer-Verlag Berlin Heidelberg 2015

AbstractMaterials with a negative Poisson’s ratio（PR）are called auxetics;they are characterized by expansion/ contraction when tensioned/compressed.Giventhiscounterintuitivebehavior,theypresentveryparticularcharacteristics and mechanical behavior.Geometrical models have been developedtojustifyandartificiall reproducesuchmaterials’auxetic behavior.The focus of this study is the exploration of a reentrant model by analyzing the variation in the PR of reentrant structures as a function of geometrical and base material parameters.It is shown that,even in the presence of protruding ribs,there may not be auxetic behavior,and this depends on the geometry of each reentrant structure.Values determined for these parameters can be helpful as approximate reference data in the design and fabrication of auxetic lattices using reentrant geometries.

KeywordsAuxetic·Poisson’s ratio·Reentrant·Finite element analysis·Elasticity

1　Introduction

Poisson’sratio（PR）isadimensionlessconstantthatdescribes the negative ratio of lateral strain to the longitudinal strain on a tensioned body.As common sense dictates,the cross section of a body becomes larger/thinner in compression/tension,so the value of this constant is assumed to be positive［1］.However,considering the classical theory of elasticity,it is possible to observe that this constant may assume values from?1 to 0.5 in three-dimensional isotropic bodies［2］and between?1 and 1 in two-dimensional isotropic materials［3］.For anisotropic materials,this constantdependsonthestretchandtransversedirectionandmay assumevaluesotherthanthepreviouslyestablishedones［4］.

MaterialsthatpresentageneralizednegativePRarecalled auxetics［5］.Anisotropic materials that reveal only negative values of PR along certain directions are called partial auxetics［6］.

Owing to the negative value of this constant,these materials are endowed with very particular characteristics and peculiar mechanical behavior［7］.Some examples are their superior resistance to indentation,shear and fracture, enhanced acoustic absorption,synclastic behavior,variable permeability,and shape memory characteristics［1］.

Some geometric models have been developed to justify this unusual behavior;among them,the most common are the reentrant,chiral,and semirigid rotating models（e.g., Ref.［7］）.It is commonly accepted that these models always demonstrate auxetic behavior;however,this may not always be true［8］.This study analyzes whether the presence of protruding ribs in a reentrant structure is enough to produce auxetic behavior in reentrant structures.

The experimental study of such models,by considering how they are made and conducting experiments on them, is an elaborate and complex task.It is convenient to resort to finite-elemen（FE）analysis to analyze them（e.g.,Refs. ［3,9］）.The use of such techniques is a very efficien and a quick way to manipulate and determine the behavior of differentreentrantmodels［10］.Consequently,theseroutines make it possible to determine the parameters that influenc the auxetic behavior of these structures.

Fig.1　a Individual cell in reentrant lattice.b Base analyzed reentrant structure

The objective of the present article is the study of the parameters that influenc the auxetic behavior of reentrant structures using FE analysis,considering the variation in the geometricalandbasematerialcharacteristics.Thisstudymay leadtothetailoringofthesestructuresandpermittheapplication of lattices（periodic structures composed by struts［11］）with a projected PR in practical applications.Additionally, the relative densities of the simulated reentrant structures will be determined considering different geometries so as to generate values of critical relative density in the transition between auxetic and nonauxetic behavior.

2　Methodology

Thefundamentalobjectiveofthisstudyisthedefinitio ofthe variables that determine the presence of auxetic behavior in a reentrant two-dimensional structure（Fig.1a）.To this end, numerical simulations（using FE analysis）were conducted to model a base reentrant structure（Fig.1b）,varying some structural characteristics and applying a quasistatic tensile load（F1）on the XX-axis（the value of the load assured that the structures never experienced plastic deformation）.This methodwasadoptedsotheinertialtermswouldbenegligible. The resultant deformations made it possible to determine the PR of the structure and,consequently,the presence/absence of auxetic behavior.

2.1Structural characteristics:geometry and base material properties

The modifie characteristics were divided into twomain categories:the geometrical and the base material parameters. In the firs category,the variation consisted in changing the length（a）,width（c）,and initial angle（β）of the ribs of the initial reentrant structures（Fig.1,Table 1）.

The base material of the structure was define as linear elastic and isotropic.This implies that its elastic behavior can be define by only two of the four basic isotropic elastic constants［12］.Inthisapproach,theselectedelasticconstants weretheYoung’smodulusandthePR.Theseconstantscompletely characterize the elastic behavior of the structures.

Given that the reentrant structures are represented in two dimensions,they were simplifiein the simulations using plane stress conditions.The other elastic constants,the bulk （K）and shear（G）moduli,can be determined considering the adopted simplificatio by Eqs.（1）and（2）［13］:

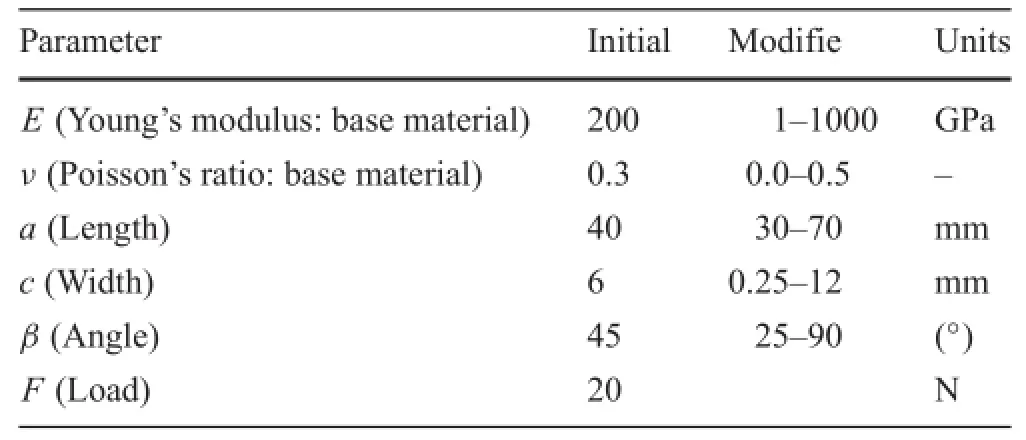
Table 1　Initial structural and modifie structural characteristics

2.2Structure simulation:finite-elemen analysis characteristics

To determine the PR of the structures,whose parameters were varied,a simulation was conducted using FE analysis.The type of simulation used was a linear elastic plane stress model,considering that the base material is isotropic. Thus,thedeformationbehaviorofthebodywasregulatedby Hooke’s law（Eq.（3））:

The stress（σ）in the structure is generated by the quasistatic unitary force（F1:Fig.1a）,applied on the XX-axis tothe structure（initially in a free body）.In isotropic materials, thetwo-dimensionalstiffnessmatrix D isdefine byEq.（4）:

Table 2　Mesh characteristics

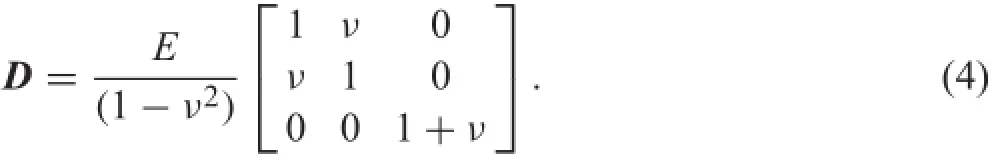
This relation implies that there are deformations imposed on the structure.The observed deformation may also be generally expressed on a given axis,in the form of strain,by Eq.（5）:

Using FE analysis,the previously define equations may be used to determine the strain of the nodes that compose the mesh in which the analyzed body is subdivided.The numericalcomputationwasperformedusingCOMSOLMultiphysics.The mesh created by that software was built using thepresetparametervaluesinthe“Extrafin mesh”function （see Table 2 for settings）.To generate the desired results, the software used the MUltifrontal Massively Parallel sparse direct Solver（MUMPS solver）.

2.3Determination of Poisson’s ratio of reentrant structures

To determine the PR of each analyzed structure and the presence/absence of auxetic behavior,the strain values were monitored in two nodes（Fig.1）.

Node 1 is placed on the axis of the imposed tensile load and will only deform in that direction（XX-axis）.Node 2 was placedsuchthatitdeformsonlyalongtheYY-axis,following theexpansion/contractionoftheprotrudingribs.Thus,bythe definitio and monitoring of these two nodes,it is possible to determine the longitudinal（XX-axis）and transverse（YY-axis）strains of each analyzed structure using Eqs.（6）and （7）:

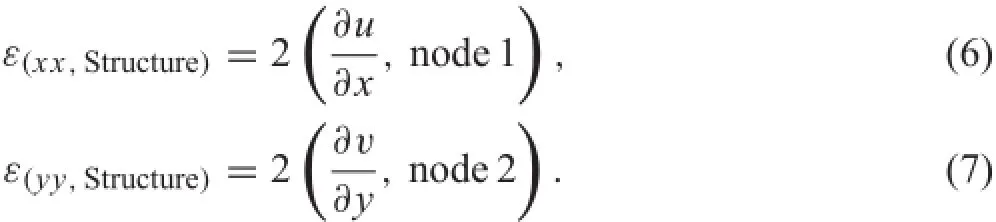
Finally,the PR of the analyzed structures can be simply determined using Eq.（8）:

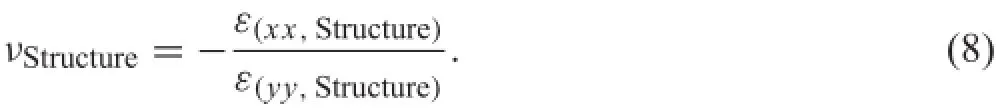
3　Results and discussion

Fig.2　Variation of structure’s PR by changing the rib width（a= 40mm,β=45?,E=200GPa,ν=0.3）

The role of the rib width was verifie（Fig.2）in the deformation mechanism of a reentrant structure.Its value was varied and numerical simulations were conducted,with the parameters mentioned previously,to calculate the PR of the individual reentrant structure.

It can be observed in Fig.2 that the rib width has a direct influenc on the value of the PR of a reentrant structure.As the rib width increases,so does the general value of the PR in a reentrant structure.

The increase in the PR with the rib width can be interpreted in the following way.When there is a small rib width, there are significan deformations even for small loads.The structure itself is not very rigid and behaves like a spring, forcing a significan vertical expansion.On the other hand, increasing the rib width will generate a stiffer structure. This change will eventually culminate in the loss of auxetic behavior,as the internal space and,consequently,the protruding ribs tend to be eliminated by the increase in the rib width.

The role of the rib length（Fig.3）was analyzed.Its value was varied and numerical simulations were conducted to determine the resulting structure’s PR.

Analyzing Fig.3,it can be observed that the rib length is a key parameter in the determination of the PR of a reentrant structure.It is shown that when the rib length increases, the actual PR of the reentrant structure decreases.This can be justifieby the spring behavior of the reentrant struc-ture.When the rib length is increased,the general structure stiffness decreases.This fact leads to significan deformations and to the vertical expansion that characterizes auxetic behavior.

Fig.3　Variation of structure’s PR by changing the rib length （c=6mm,β=45?,E=200GPa,ν=0.3）

Fig.4　Variation of structure’s PR by keeping the rib’s AR at 5 （β=45?,E=200GPa,ν=0.3）

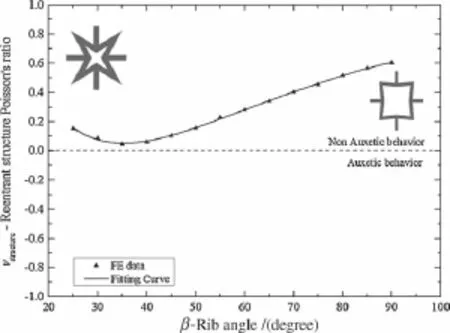
Fig.5　Variation of structure’s PR by changing the rib angle （a=40mm,c=6mm,E=200GPa,ν=0.3）

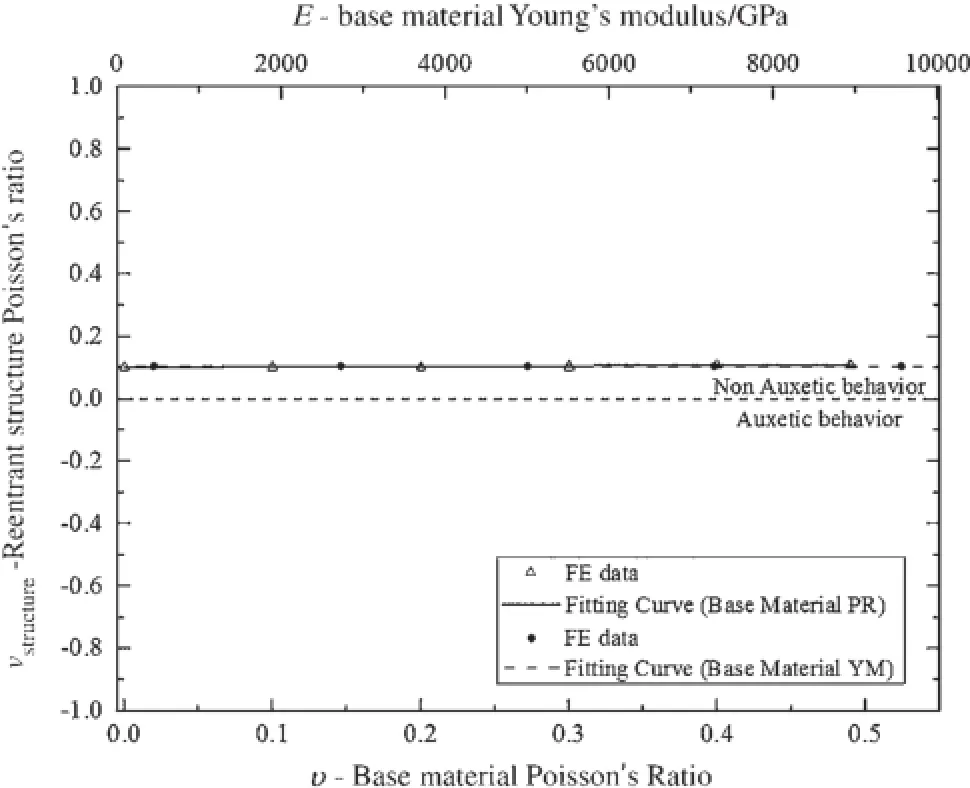
Fig.6　Variation of structure’s PR by changing the base material PR and Young’s modulus（a=40mm,c=6mm,β=45?）

Observing the previous results in Fig.3,it can be concluded that the auxetic behavior of a reentrant structure dependsontheriblengthandwidth.Thesevaluesaremainly related to the length and width of the ribs,which will determine the stiffness of the structure.Therefore,simulations were conducted to determine the dependence of the PR of the structure on the aspect ratio（AR）between the length and the width of a structure’s ribs（Fig.4）.The value of the rib length was varied,but the proportion of the AR was kept constant at a value of 5.

According to Fig.4,it can be observed that when the AR is kept constant,the PR of the structure remains constant as well.

Anotheranalyzedparameterwastheinitialanglebetween ribs,as shown in Fig.5.Numerical simulations were conducted with different values of the initial angles,and the importance of a reentrant structure in the deformation mechanism was verified

Observing Fig.5,it can be concluded that the PR of a reentrant structure is influence by the initial angle between ribs.When the angle decreases,there is a similar decrease in the value of the structure’s PR.However,for extremely low values of rib angles,the PR increases.A decrease in the rib anglegeneratesadecreaseinthefreeinteriorstructuralspace. In extreme cases,this space ceases to exist,eliminating the reentrant structure.

Proceeding to the base material parameters,the PR and Young’s modulus of the base material were analyzed to determine their influenc on the deformation behavior of a reentrant structure.Geometrical equivalent base structures were simulated based on Fig.1b,varying the PR and the Young’s modulus of the base material.The results are presented in Fig.6.

ItisshownthePRofthereentrantstructureremainsstable when the PR of the base material is changed.Note that thetwo do not predominate when describing the deformation mechanism of a reentrant structure.

Table 3　PR of reentrant structure for different ARs and rib angles （E=200GPa,ν=0.3）

As may be observed,the value of the PR of the reentrant structure remained constant when the Young’s modulus of the base material was changed.In this way,it is shown that the PR of a reentrant structure is independent of the value of the Young’s modulus of the base material.

Having isolated all the fundamental parameters that describe the deformation mechanism of a reentrant structure,we can establish that the auxetic behavior will mainly depend on the interaction of the length,width,and angle of the ribs.Because the PR of a reentrant structure remains constant for the same rib AR,these two parameters can be analyzed using only one ratio.With the facts presented,and carryingoutnumericalsimulations,theobtainedinformation was used to create Table 3.

LookingatTable3,itcanbeobservedthatthereisadependencebetweentheauxeticbehavior,lowvaluesofribangles, and high values of AR.

According to the executed simulations and the resulting data,it was possible to elaborate Fig.7.Boundaries relating the structure’s AR and initial rib angle were established that might predict whether a reentrant structure will demonstrateauxeticbehaviorandshowthespecifi valuesof the PR.

In terms of relative density,it can be observed in Fig.8 thatthevaluesofARandinitialribanglegenerateaparabola shape function.When the values of the initial rib angle are extreme（either high or low）,the values of the relative density tend to decrease.However,only low values of AR tend to increase this effect.It can also be observed that each AR that demonstrates auxetic behavior has a specifi value of the critical relative density where the transition between auxetic/nonauxetic behavior takes place.Considering the aforementioned plots,it is suggested that the value of the critical density is lower in the presence of a low AR.In contrast,for low initial rib angles the value of the critical relative density tends to increase.Given that a low AR implies thinner and longer ribs,the overall relative density tends to decrease.However,in the case of the initial rib angle,the structure tends to fold on itself,closing the opening in its interior and generating higher relative density values.

Fig.7　Variationofstructure’s PR using the ribangle fordifferent ARs

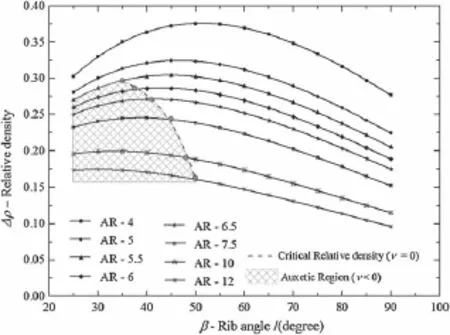
Fig.8　Relativedensityofreentrantstructuresasafunctionofribangle and AR

4　Conclusions

Considering the results of the executed numerical simulations,it was shown that a reentrant structure,even in the presence of protruding ribs,may not always demonstrate auxetic behavior.This study isolated the length,width （mainly the AR）,and initial angle of the structure’s ribsas the predominant factors that determine auxetic behavior.It was also observed that the characteristics of the base material that composes the structures,such as the constants that describe elastic deformation,may have less influencon the auxetic behavior of a reentrant structure.

Limits to the values of length,width,and angles of the ribs were define to obtain and tailor a predetermined value of the PR of these structures.This allows for the development of structures with a definePR,even in the project phase,using the same base geometry.According to this formulation,the obtained value of PR is directly related to the unitary reentrant structure.In the case of their application in a lattice,the obtained value of the macroscopic PR may vary slightly,given that the ribs that connect the individual reentrant structures are also elastic.However,as thepresentstudysuggests,themaindeformationmechanism used to induce auxetic behavior is the bending of the protruding ribs,and this implies a low AR of the ribs.The elastic deformation of the ribs that connect each individual reentrant structure（the ones that do not protrude）is mainly the result of tensile and compressive forces.This last forces,in connection with macroscopic deformation,are negligible compared to the overall reentrant structure expansion.

Additionally,the value of the critical relative density at which the transition between auxetic and nonauxetic behavioroccurswasdetermined.Itwasshownthatthisvaluetends to increase for lower initial rib angles.However,in the presence of a low AR,the value of the critical relative densities tends also to decrease.The generated values of the relative density may also be used in a project phase as an input on weight and overall structural performance when projecting an auxetic lattice.

References

1.Carneiro,V.H.,Puga,H.,Meireles,J.:Auxeticmaterials—areview. Mater.Sci.Pol.31,561-571（2013）

2.Mott,P.H.,Roland,C.M.:Limits to Poisson’s ratio in isotropic materials—generalresultsforarbitrarydeformation.Phys.Scr.87, 055404（2013）

3.Strek,T.,Maruszewski,B.,Narijczyk,J.W.,et al.:Finite element analysisofplatedeformation.J.Non-cryst.Solids354,4475-4480 （2008）

4.Norris,A.N.:Extreme values of Poisson’s ratio and other engineering moduli in anisotropic materials.J.Mech.Mater.Struct.1, 793-812（2006）

5.Dirrenberger,J.,Forest,S.,Jeulin,D.:Elastoplasticity of auxetic materials.Comput.Mater.Sci.64,57-61（2012）

6.Bra′nka,A.C.,Heyes,D.M.:Ma′ckowiak,Sz,etal.:Cubicmaterials in different auxetic regions-linking microscopic to macroscopic formulations.Phys.Status Solidi B 249,1373-1378（2012）

7.Critchley,R.,Corni,I.,Wharton,J.A.,etal.:Areviewofthemanufacture,mechanicalpropertiesandpotentialapplicationsofauxetic foams.Phys.Status Solidi B 250,1963-1982（2013）

8.Liu,Y.,Hu,H.:Areviewinauxeticstructuresandpolymericmaterials.Sci.Res.Essays 5,1052-1063（2010）

9.Bückmann,T.,Schittny,R.,Thiel,M.,et al.:On three-dimensional dilational elastic metamaterials.N.J.Phys.16,033032（2014）

10.Pozniak,A.A.,Smardzewski,J.,Wojciechowski,K.W.:Computer simulations of auxetic foams in two-dimensions.Smart Mater. Struct.22,084009（2013）

11.Fan,H.-L.,Zeng,T.,Fang,D.-N.,et al.:Mechanics of advanced fibe reinforced lattice composites.Acta Mech.Sin.26,825-835 （2010）

12.Du,D.X.,Zheng,Q.S.,Gao,Y.X.:Consistency between independence theorems and generalized self-consistent method.Acta Mech.Sin.13,355-365（1997）

13.Jasiuk,I.,Chen,J.,Thorpe,M.F.:Elasticmodulioftwodimensional materialswithpolygonalandellipticalholes.Appl.Mech.Rev.47, 18-28（1994）

28 September 2014/Revised:15 March 2015/Accepted:16 April 2015/Published online:17 November 2015

?V.H.Carneiro

vitorhcarneiro@hotmail.com

1Department of Mechanical Engineering,University of Minho, Campus de Azurem,4804-533 Guimar?es,Portugal