Kinematic Optimization of Bionic Shoulder Driven by PneumaticMuscle Actuators Based on Particle Swarm Optimization
Liu Kai, Ge Zhishang, Xu Jiaqi, Gu Baotong, Wang Yangwei, Zhao Dongbiao
College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics andAstronautics, Nanjing 210016, P.R. China
(Received 4 November 2015; revised 24 December 2015; accepted 28 December 2015)
Kinematic Optimization of Bionic Shoulder Driven by PneumaticMuscle Actuators Based on Particle Swarm Optimization
Liu Kai*, Ge Zhishang, Xu Jiaqi, Gu Baotong, Wang Yangwei, Zhao Dongbiao
College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics andAstronautics, Nanjing 210016, P.R. China
(Received 4 November 2015; revised 24 December 2015; accepted 28 December 2015)
A bionic shoulder joint with three degree-of-freedom (DOF) driven by pneumatic muscle actuator is proposed and its corresponding kinematic model is established. The bionic shoulder is optimized by particle swam optimization (PSO) with the fitness standards that the requirements of rotation indexes are met and the fluctuation of motion is kept in the lowest resolution in a pneumatic muscle actuator range. Simulation considering rotation indexes only (first simulation) is compared with the one considering both rotation indexes and motion resolution (second simulation) subsequently. Mounting position of the pneumatic muscle actuators in bionic shoulder is optimized after initializing the same condition in simulations. Results show that the fluctuations of parameters are consistent, and the parameters of the first simulation have good convergence than those of the second one. With the increase of stretch rate of the pneumatic muscle actuator, the needed length of fixed link in the center of static platform decreases in optimization.
bionic shoulder joint; particle swam optimization (PSO); kinematic optimization
0 Introduction
The shoulder joint is the most flexible joint rotating in three-degree-of-freedom (3-DOF) (Fig.1), which can realize the motions of abduction, adduction, lateral rotation, medial rotation, flexion and extension. While motions of different people are not the same as the differentiated bones, the motion indexes such as the degree of abduction, adduction, lateral rotation (when abduction degree is 90°), medial rotation (when abduction degree is 90°), flexion and extension are appropriately defined as 180°, 180°, 90°, 90°, 180° and 180°, respectively.
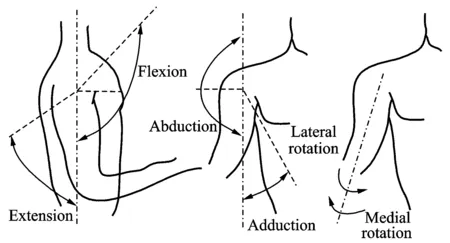
Fig.1 Rotation motion of shoulder joint
The study of bionic shoulder joint has come to its climax in recent years. A 3-RRR (′R′ is expressed as a revolute pair) mechanism suitable for shoulder was proposed by Yi[1]. Hou[2]improved the suitability of 3-RRR for shoulder in the base of traditional 3-RRR mechanism. A 3-DOF shoulder driven by muscles was designed by Garner[3]under the consideration of the visible human project image dataset, and then dynamic optimization of the shoulder was analyzed by Terrier[4]. A kind of 3-DOF shoulder possessing scapula, clavicle and humerus was put forward by Sodeyama[5]. In spite of the fact that all mechanisms mentioned above are capable of three degrees of rotation, they either have simple structure without the flexibility or complicated structure that cannot be controlled easily.
The pneumatic muscle actuator (PMA)[6]is a new kind of actuators powered by pressure, and its durability and strength has been improved since the emergence of PMA in 1960 s. PMAs are highly applicable for the actuators in bionic research, because they have impressive power-to-weight and power-to-volume ratios and provides natural flexibility[6-8]similar to biological muscles. PMAs capable of producing high force have application in many areas, but are of particular interest in human interactive environment.
Recently, the optimization of parallel mechanism has been hot research topics. Several optimization algorithms, such as genetic algorithm (GA), particle swarm optimization (PSO), simulated algorithm (SA) and adaptive simulated algorithm (ASA), are employed to design parallel mechanism. According to motion, force, and power distribution performance indicators, Zhang[9]optimized the structural parameters of 3-RPS (′R′ is expressed as a revolute pair, ′P′ as a prismatic pair, and ′S′ as a spherical pair) parallel mechanism and got the corresponding workspace. A 3-PCSS/S (′PC′ is expressed as a prismatic pair with a ring rail, and ′S′ a spherical pair) spherical parallel mechanism for the shoulder joint is proposed by Hou[10]. They optimized its parameters of the mechanism and improved its flexibility with GA. Zhang[11]obtained the optimal particle which was optimized by means of the improved chaotic PSO and improved motion performance of Ahut-Delta. Sun[12]analyzed the impact of main parameters in PSO upon the search of particles and used PSO in parameter optimal design of six degrees-of-freedom (DOF) parallel mechanism.
Particle swarm optimizer was presented by Kennedy and Eherhart in 1995 on the basis of evolvement analysis of intelligent control[13-14]. Shoulder joint powered by parallel mechanism has several motion indexes which cannot be satisfied simultaneously, but PSO is a way of multi-objective optimization which is well suitable for shoulder joint optimization.
A bionic shoulder joint driven by six pneumatic muscle actuators is proposed in this paper. By using the optimization of PSO, the shoulder joint can optimize its structure with the optimization goal that motion indexes are satisfied and motion resolution of joint is reduced minimally in the contraction range of PMA.
1 Kinematic Model for Bionic Shoulder
Two coordinate frames are defined for analysis. The base coordinate frame {A}: XYZ is attached to the geometric center of static platform O with its Z-axis perpendicular to the plane defined by the actuator base points A1A2A3A4A5A6and X-axis parallel to A1O. The moving coordinate frame {B}: xyz is attached to an endpoint (O1) of the link installed in the geometric center of moving platform with its z-axis perpendicular to the plane of B1B2B3and x-axis parallel to B1B. The degree of bionic shoulder is, apparently, determined by spherical joint defined as O1in Fig.2, so its degree is three as spherical joint can rotate in three perpendicular axes.
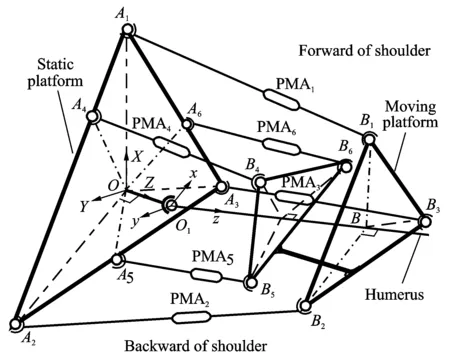
Fig.2 Geometric model for bionic shoulder
The direction of forward/backward shoulder is shown in Fig.2. The angle of the moving platform rotating around Y-axes from OY-to OY+is the abduction angle. Let the angle of the moving platform rotating around Z-axes in a clockwise direction and an anticlockwise direction be, respectively, the medial rotation (abduction degree is 90°) and lateral rotation (abduction degree is 90°) when the moving platform do not rotate around
X-axes and Y-axes. Assume that the degree of moving platform rotates around Z-axes in the clockwise direction and the anticlockwise direction, respectively, is the degree of extension and the degree of flexion when moving platform rotates around Y-axes to OY-. OY+and OY-mean the maximum degrees in which the moving platform rotates clockwise and anticlockwise around Y-axes, respectively.
The coordinate of point Biin the moving frame can be written as
(1)
The coordinate of point Aiin the base frame can be written as
(2)
whereθiis the same value shown in Eq.(1).
The position of point O1in the moving platform is defined
(3)
(4)
where γ, β and α are the orientation angles of the moving platform denoting rotations of the moving coordinate frame about the X-axes, Y-axes and Z-axes in the base coordinate frame, respectively.
(5)
Hence, the length of pneumatic muscle actuator can be calculated as
(6)
where Aiand Biare the coordinate expressed in Eqs.(1), (2).
The φ in Eq.(1) and η in Eq.(2) are the structural parameters determining the characterization of singularity. If φ=η, the bionic shoulder stays in a singular state in initial position. More details about it is that the moving platform cannot rotate around the static platform in Z-axes when γ=0, β=0 and α=0. If φ≠η, the moving platform is able to rotate around the Z-axes when γ=0, β=0 and α=0.
2 Kinematic Optimization Aim of Bionic Shoulder
The bionic shoulder is a spatial parallel mechanism which can be optimized in manipulability, space utilization[15]and motion resolution[16]. Considering the actual features of the bionic shoulder, rotation indexes and motion resolution are optimized in the contraction range of PMA.
2.1Constraint function of rotation indexes about bionic shoulder
After the numerical values of the dimensions are entered through parameters input interfaces, the geometric model will then complete. In this way, a repeatable and standard modeling method is created to avoid the tedious modeling process in ANSYS. The structure dimensions are displayed in Fig.2.
Rotation indexes are the abduction angle, adduction angle, the degree of lateral rotation (when abduction degree is 90°), the degree of medial rotation (when abduction degree is 90°), the flexion degree, and the degree of extension. The constraint function of rotation indexes can be described as

w4C4+w5C5
(7)
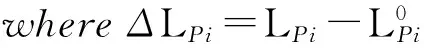
(8)
where φaid, φaed, φad, φatd, φprdare the desirable lateral rotation degree, the desirable medial rotation degree, the desirable abduction degree, the desirable flexion degree, and the desirable extension degree, respectively. φai, φae, φa, φatand φprare the calculated lateral rotation degree, the calculated medial rotation degree, the calculated abduction degree, the calculated flexion degree, and the calculated extension degree, respectively.
2.2Constraint function of motion resolution about bionic shoulder
The micro displacement of any point Q(x, y, z) in B1B2B3can be transformed into three micro displacements of coordinate axis in the base coordinate frame, and their relation can be expressed as
(9)
Any displacement in Eq.(9) can be transformed into three micro rotational angles of coordinate axis, expressed as
(10)
Substituting Eq.(10) into Eqs.(9) yields Eq.(11).
(11)
(12)
(13)
The point Biin the base coordinate frame can be expressed as
(14)
The motion resolution relative to r ofABi(i=1—3) in B1B2B3can be calculated by
(15)
(16)
(17)
where μ=L/r,k1=cos2θcos2β+sin2θsin2βsin2γ+sin2θcos2γ,k2=μ2sin2βcos2γ+μ2sin2γ+2sinθcosθsinβcosβsinγ+2μcosθsinβcosβcosγ, k3=2μsinθsin2βsinγcosγ-2μsinθsinγcosγ.
(18)
where
(19)
(20)
(21)
Eq.(18) can be used to evaluate the fluctuation of motion resolution. The parameter n in Eqs.(19)—(21) is the number of micro rotations around X-axes, Y-axes, and Z-axes, respectively.
The pointABi(i=4—6) in B4B5B6can also achieve the fluctuation of motion resolution relative to rcby the method mentioned above.
(22)
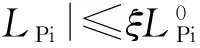
3 Optimization Model of PSO
The core idea of PSO is that all particles can update their locations and velocities according to the position vector, the velocity vector, the best positions of particles and the best positions of population in any iteration, so the population can acquire the optimal solution in N iterations[17-18]. The algorithm can be described as follows.
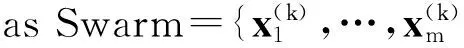
(23)
(24)
(25)
where i=1—m, d=1—D. c1and c2are the two acceleration constants weighting of the random acceleration terms, r1and r2the random numbers from 0 to 1, and ω the inertia coefficient.
In order to keep the convergence of velocity, the velocity vector should meet the constraint shown in Eq.(26).
(26)
4 Two Cases of Kinematic Optimization of Bionic Shoulder
Case 1Only consider the rotation indexes into fitness function.
(27)
(28)
Eq.(28) works when the ffit1values of two particles are equal.
Case 2Consider the rotation indexes and motion resolution into fitness function
(29)
Particles are updated on condition that one of them (ffit3and ffit4in Eq.(29)) is met and the other is equal or both of them are met.
Assuming that a particle has a nine-dimensional vector x=(R,Rc,r,rc,l,L,Lrc,η,φ), and the swarm has P=50 particles, with the iteration of N=40, learning factors of c1=c2=1.494, contraction ratio of ξ=0.1, inertia coefficient of ω=0.5+rand()/2, where rand() is the function of a random number generator uniformly distributed in [0,1], and weight values w1=w2=10,w3=5,w4=w5=1.
Assuming the constraint boundary
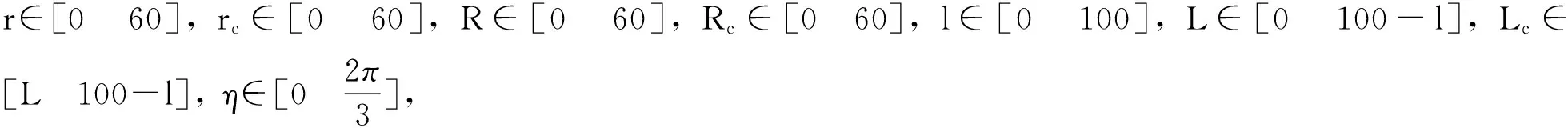
Desirable rotation values are
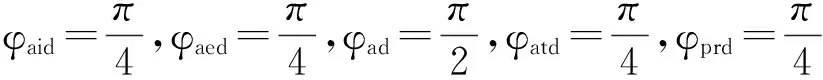
Velocity constraint values are
According to the initial condition and constraint, four random simulation results of Case 1 and Case 2 are shown in Tables 1, 2. It is depicted that the number of iteration in Case 1 is less than that in Case 2. Most of optimal results in Case 1 are occurred in the first iteration. In contrast, in view of the motion resolution in Case 2, more iterations are needed to get optimal results. From the above simulation, it is shown that desirable rotation value can be obtained, but further simulations depict that once φad>π/2 (or φaed>π/4, or φatd>π/4, φprd>π/4), one or more parameter (R, Rc, r, rc, l, L, Lrc, φ, η) cannot be acquired from this optimization.
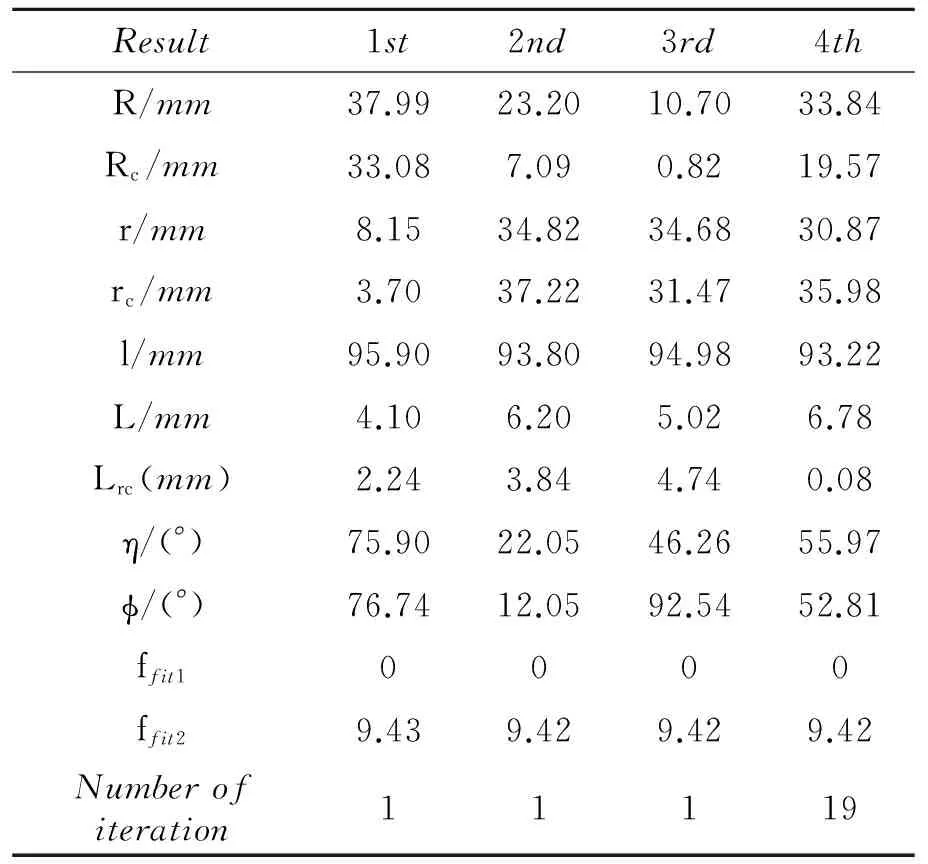
Table 1 Four random simulations for Case 1

Table 2 Four random simulations for case 2
R, Rc, r, r, l, L, Lrc, η and φ are coupled with each other. The subtle change of one parameter can alter the turning angle. For example, in the first simulation of Table 1, φaid, φaed, φad, φaidand φprdcan meet the desirable rotation value. However, once one parameter changes (l=94 mm), φaedcannot achieveπ/4 but onlyπ/6. In the first simulation of Table 2, if r=15 mm, φadcannot reachπ/2 but onlyπ/3.
The kinematic optimization of bionic shoulder focuses on the reachability in space, and more optimal results can be calculated when the same fitness value occurs. Fluctuation of nine variables is obtained by calculating variance of 50 simulations in four groups and the results in Cases 1, 2 are shown in Figs.3, 4, respectively. It is demonstrated that the fluctuation of R, Rc, r and rcappears to be uniform: fluctuation of the four variables increases or decreases synchronously, that is to say, they are coupled with each other. This phenomenon is reasonable in that as the result of the limitation of contraction ratio of PMA, the change of one variable may cause others adjusting in the optimized range. Fluctuations of η and φ in Case 1 is less than those of η and φ in Case 2, which indicates that the consideration of motion resolution in Case 2 has great effect on the convergence of η and φ. The reason why the fluctuation of l and L is same lies in that (l+L) is a constant.
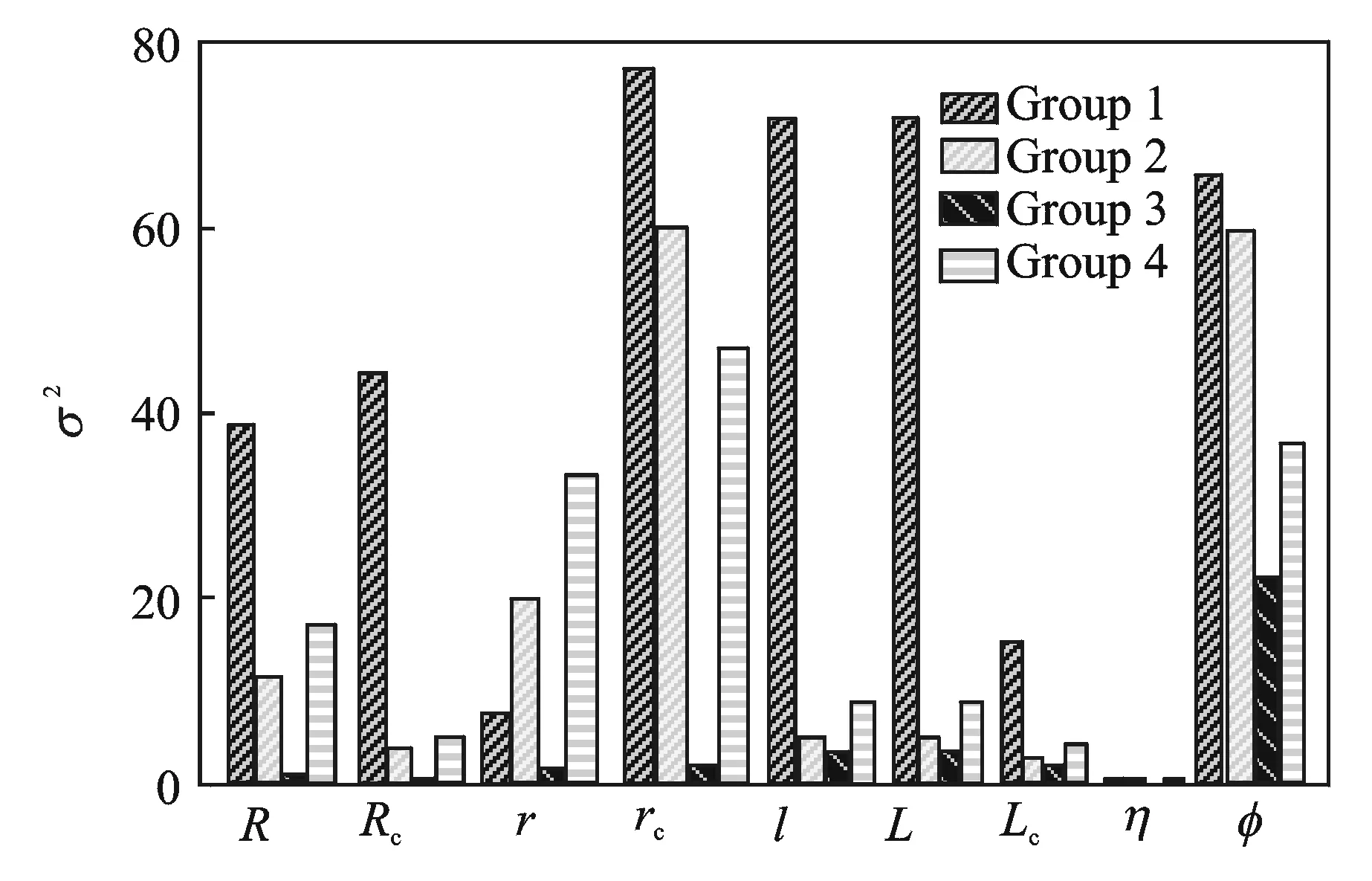
Fig.3 Fluctuation simulation of four groups in Case 1
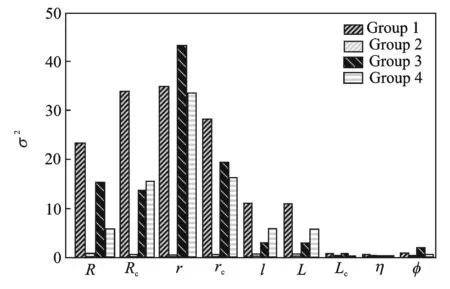
Fig.4 Fluctuation simulation of four groups in Case 2
In the eight simulations shown in Tables 1, 2, it can be seen that l approaches to a limit value L. A new simulation about the contraction ratio ξ to l in the optimized condition is done in the same condition mentioned above. Results shown in Fig.5 reveal that the needed parameter l in the optimized condition decreases with the increase of ξ and the needed l in Case 1 is smaller than the needed l in Case 2 at the same ξ.

Fig.5 Relationship between ξ and l
Particle swarm optimization (PSO) and genetic algorithm (GA) are both optimization algorithms. Both of them can simulate the adaptability of individual population on the basis of natural characteristics. Compared with conventional optimum evaluation methods, for instance, the Powell method, they can improve the searching efficiency in the whole field by gradually shrinking the area of design variables.
For Case 1, in order to prove rationality of PSO in this paper, we compare the results of optimization of two algorithms (PSO & GA), as shown in Tables 1,3.
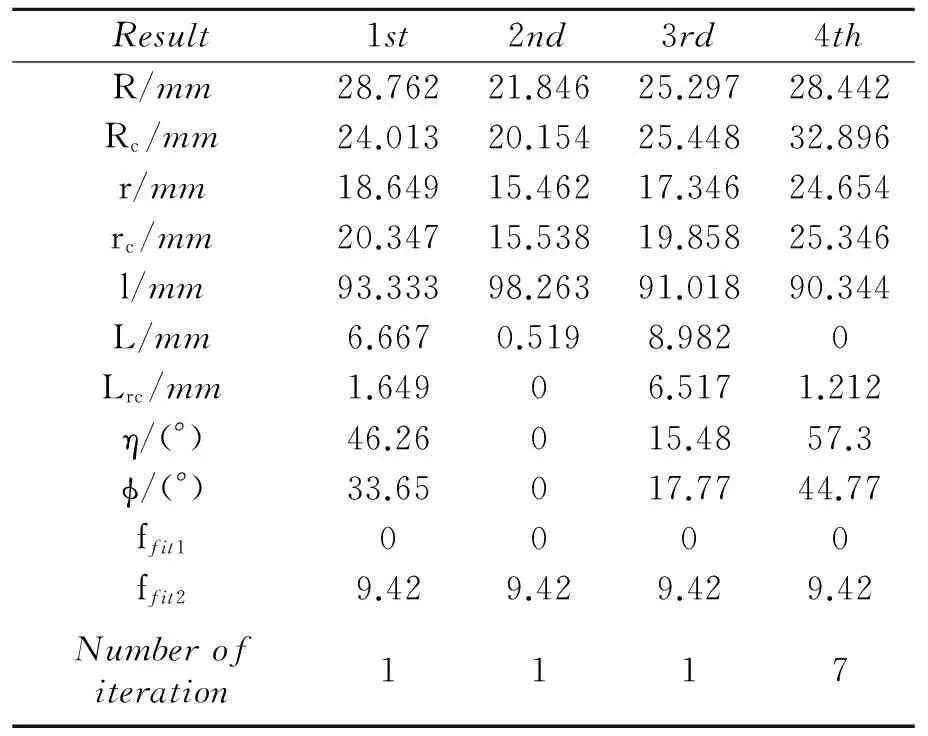
Table 3 Four random simulations for case 1 with GA
It is found that both of these two methods can quickly achieve the optimization so that meet the requirements of performance. Compare with GA, PSO is easier to implement with less parameters to adjust. Obviously, it is feasible and reasonable to apply PSO to the structural optimization.
5 Conclusions
A 3-DOF bionic shoulder driven by six pneumatic muscle actuators was proposed in this paper and the relationship between the three-dimensional rotations of shoulder and the length of six pneumatic muscle actuators was constructed.
Rotation indexes about abduction, adduction, etc. of the bionic shoulder were defined by bionic model. The bionic shoulder was optimized by means of PSO in the fitness standards that requirements of rotation indexes are met and fluctuation of motion resolution is kept in a lower level in the contraction range of PMAs.
A comparing simulation between considering rotation indexes only (Case 1) and considering both rotation indexes and motion resolution (Case 2) was conducted. Conclusions from further simulation results show that R, Rc, r, and rcappear to be uniform and the fluctuation of η and φ is tiny. Finally, from the simulation of ξ - l, it was found that l needed in the optimal condition decreases with the increase of ξ. In addition, the comparison results about Case 1 between PSO and GA show that PSO is feasible and satisfactory in the design of the parallel mechanism.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No.51405229), the Natural Science Foundation of Jiangsu Province of China (No.BK20151470), and the NUAA Fundamental Research Fund (No.NS2013049).
[1]YI B J, FREEMAN R A, TESAR D. Force and stiffness transmission in a redundantly actuated mechanism: The case for a spherical shoulder mechanism[J]. ASME, Design Engineering Division, 1992,45:163-172.
[2]HOU Y L, HU X Z, ZHOU Y L. Bionic joint design based on a novel over-constrained spherical parallel mechanism[J]. Chinese Mechanical Engineering, 2014,25(6):723-726.
[3]GARNER B A, PANDY M G. A kinematic model of the upper limb based on the visible human project (VHP) image dataset[J]. Computer Method in Biomechanics and Biomedical Engineering, 1999,2(2):107-124.
[4]TERRIER A, AEBERHARD M, MICHELLOD Y, et al. A musculoskeletal shoulder model based on pseudo-inverse and null-space optimization[J]. Medical Engineering & Physics, 2010,32(9):1050-1056.
[5]SODEYAMA Y, NISHINO T, NAMIKI Y, et al. The designs and motions of a shoulder structure with a spherical thorax, scapulas and collarbones for humanoid Kojiro[C]∥RSJ International Conference on Intelligent Robots and Systems. France: IEEE, 2008:1465-1470.
[6]DAERDEN F, LEFEBER D, VERRELST B, et al. Pneumatic artificial muscles: actuators for automation and robotics[C]∥Proceedings of the 2001 IEEE/ASME International Conference on Advanced Intelligent Mechatronics. New York: IEEE, 2001:738-743.
[7]TAO G L, XIE J W, ZHOU H. Research achievement and development trends of pneumatic artificial muscles[J]. Chinese Journal of Mechanical Engineering, 2009,45(10):75-83.
[8]SUI L M, WANG Z W, BAO G. Analysis of stiffness characteristics of the pneumatic muscle actuator[J]. Chinese Mechanical Engineering, 2004,15(3):242-244.
[9]ZHANG L J, GUO F, LI Y Q, et al. Optimun design of parallel mechanism based on kinematics distribution performance[J]. Transactions of the Chinese Society for Agricultural, 2015,46(4):365-371.
[10]HOU Y L, WANG Y, FAN J K, et al. Optimization and bionic design of 3-PCSS/S spherical parallel mechanism for the shoulder joint[J]. Journal of Mechanical Engineering, 2015,51(11):16-23.
[11]ZHANG L A, WANG J, TAN Y L. Dimensional synthesis of ahut-delta parallel mechanism based on improved chaotic particle swarm algorithm[J]. Transactions of the Chinese Society for Agricultural, 2015,46(8):344-351.
[12]SUN F G, HUANG W. Parameter optimal design of the parallel mechanism based on particle swarm optimization[J]. Machine Design and Research, 2006,22(3):16-18.
[13]KENNEDY J, EBERHART R C. Particle swarm optimization[C]∥Proceedings of IEEE International Conference on Neural Networks. New York: IEEE, 1995:1942-1948.
[14]LIU S, WANG T, FAN W, et al. Optimization of joint driven by pneumatic muscle actuator based on PSO algorithm[J]. Journal of Beijing Institute of Technology, 2012,32(1):47-50.
[15]STOCK M, MILLER K. Optimal kinematic design of spatial parallel manipulators: application to linear delta robot[J]. Transactions of the ASME, 2003,125(2):292-300.
[16]SUN L N, DING Q Y, LIU X Y. Optimal kinematic design of 2-DOF planar parallel robot with high speed and high precision[J]. Chinese Journal of Mechanical Engineering, 2005,41(7):95-97.
[17]ZHANG L H, YAO S Q, XIE W C. Voice conversion based on adaptive particle swarm optimization radial basis function neural network[J]. Journal of Data Acquisition and Processing, 2015,30(2):336-343.
[18]GU W B, TAN D B, ZHENG K. Solving job-shop scheduling problem based on improved adaptive particle swarm optimization algorithm[J]. Trans. Nanjing Univ. of Aeronaut. Astronaut., 2014, 31(5):559-567.
Dr. Liu Kai is an associate professor at College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics (NUAA), China. He received his Ph.D. degree from NUAA in 2007. His main research interest is bionic robot and numerical control technology.
Mr. Ge Zhishang received his B.Sc. degree from Shenyang Ligong University, China, in 2014. He is currently pursuing master degree in Nanjing University of Aeronautics and Astronautics. His research interests are primarily in the area of motion control and bionic robot.
Mr. Xu Jiaqi received his B.Sc. degree from Nanhang Jincheng College, China, in 2015. He is currently pursuing master degree in NUAA. His research interests are primarily in the area of motion control and robotics.
Mr. Gu Baotong received his M.Sc. degree from NUAA in 2015. His research interests are primarily in the area of motion control and measurement system.
Dr. Wang Yangwei received his M.S. degree and Ph.D. degree from Harbin Institute of Technology (HIT), China. He is currently a lecturer at the College of Mechanical and Electrical Engineering at NUAA in Nanjing, China. His research interests include bionic robot, robotics, and control system.
Dr. Zhao Dongbiao received his M.S. degree and Ph.D. degree from Nanjing University of Aeronautics and Astronautics (NUAA), China. He is currently a Professor at the College of Mechanical and Electrical Engineering at NUAA in Nanjing, China. Dr. Zhao's research interests include CNC system, robotics, and control system.
(Executive Editor: Zhang Tong)
, E-mail address: liukai@nuaa.edu.cn.
How to cite this article: Liu Kai, Ge Zhishang, Xu Jiaqi, et al. Kinematic optimization of bionic shoulder driven by pneumatic muscle actuators based on particle swarm optimization[J]. Trans. Nanjing Univ. Aero. Astro., 2016,33(3):301-309.
http://dx.doi.org/10.16356/j.1005-1120.2016.03.301
TH138; TP242Document code:AArticle ID:1005-1120(2016)03-0301-09
 Transactions of Nanjing University of Aeronautics and Astronautics2016年3期
Transactions of Nanjing University of Aeronautics and Astronautics2016年3期
- Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Advances in Technologies of Piezoelectric Pumping with Valves
- Numerical Optimization on Aerodynamic/Stealth Characteristics of Airfoil Based on CFD/CEM Coupling Method
- Kinematic Calibration of Asymmetricly Actuated 6-DOF 3-PPPS Parallel Mechanism
- Dynamic Modeling and Adaptive Fast Nonsingular Terminal SlidingMode Control for Satellite with Double Rotary Payloads
- A Comprehensive Review on RNA-seq Data Analysis
- Joining Force of Heterogeneous Titanium Alloy in Linear Friction Welding Process
