An Improved Discrete-Time Model for Heterogeneous High-Speed Train Traffic Flow?
Yan Xu(許琰),Bin Jia(賈斌),,? Ming-Hua Li(李明華),and Xin-Gang Li(李新剛)
1State Key Laboratory of Rail Traffic Control and Safety,Beijing Jiaotong University,Beijing 100044,China
2School of Traffic and Transportation,Beijing Jiaotong University,Beijing 100044,China
1 Introduction
With the rapid economic development in recent years,demands for high-speed passenger railway transportation become greater and greater.The high-speed passenger railway in China has entered into a period of rapid development.It is predicted that high-speed railway in China may increase to more than 18,000 kilometers till 2020,which will be more than half of the total mileage of highspeed railway in the world.However,the ability of infrastructure construction is limited,while the demands of the railway traffic become more and more.Hence,how to utilize the limited resources to meet the increasing traffic demands,and what is the relationship between railway traffic capacity,train travel velocity and other characteristics of railway traffic flow have attracted the attention of a community of scholars.[1?13]As mentioned in Refs.[3–7],when the train density of railway line reaches a certain degree,it will form the train traffic flow and the trains interact with each other.Accordingly,some characteristics of train traffic flow,including the traffic capacity,velocity,etc.,can be analyzed drawing on the experience of macroscopic traffic flow theory for road traffic flow on the base of numerical results.Meanwhile,train movements,mainly related to train control strategy,energy consumption,operation safety,etc.,can well reflect dynamical characteristics of trains running on the railway line.So,these has been the main motivation for us to explore an efficient simulate model for train movements,aiming to investigate the characteristics of the high-speed passenger train traffic flow.
Up to now,many models and methods have been proposed to depict train movements,including cellular automata(CA)model,[1?5,13]discrete-time model(DTM),[6?7,14]discrete-event model(DEM),[8?10,16]carfollowing model,[15]etc.In 2005,Li et al.[1?2]firstly applied CA theory to the railway system by changing update rules.After that,Zhou et al.[3]developed a new CA model to simulate train traffic flow under the quasi-moving block system,and then analyzed the effect of departure time intervals and train delays propagation mechanism.Fu et al.[4]established a CA model for train movements in fi xed block system,and investigated the performance of the Beijing metro line 2.Xu et al.[5]developed an equation of minimum safety headway under moving block system to depict train movements and some characteristics of train traffic flow were captured.Along with the development of CA theory,a discrete-time movement model(DTM)was introduced by Yang et al.[6]by taking the stochastic disturbances of train traffic flow into consideration,but only the homogeneous train traffic flow was discussed in their work.By utilizing the DTM,Sun et al.[7]simulated the mixed high-speed train movements on double-track railway line and analyzed some characteristics of railway traffic flow.Apart from that,Dorfman and Medanic[8]classified the interaction events among trains into a few categories,for instance meet event,overtaken event,etc.and then firstly proposed a discrete-event model(DEM)to schedule two-way railway train traffic on single-track and train movements were controlled by local feedback-based travel advance strategy(TAS).Li et al.[9]improved the TAS to global feedback-based travel advance strategy for scheduling trains on single-track line.While,Xu et al.[10]proposed a rigorous optimization model with consideration of velocity variation,aims to find the optimal velocity for each train running on the railway line.Unfortunately,these research works as mentioned above were about the normal train traffic flow,i.e.,the researchers did not take into account the effects of the traffic interruption.Actually,in daily traffic flow,traffic failure,for instance traffic accident,road maintenance,etc.,happens at a certain probability,then the phenomena of traffic flow become more complicated.Tang et al.have considered the traffic interruption in the road traffic flow model.[11?12]They presented a new macro model which involves the effects of the traffic interruption probability on the car-following behavior through formulating the inner relationship between micro and macro variables.[11]After that,they further presented a new car-following model by considering the effects of the traffic interruption.[12]Similarly,considering the train failure during daily operation,Zhang et al.[13]presented a new CA model to simulate the occurrence of the train failure and reproduced the complex behaviors of train movements in railway transit system.Recently,some scholars[14?16]attempted to optimize train movements by taking energy consumption into account.
In the existing CA models for simulating train traffic flow,the space of the railway line was split into discrete cells so the value of velocity and acceleration needs to be integer.Obviously,the CA model was confined to describe train’s non-integral velocity/acceleration in train movements on the railway line.While,in the model proposed by Sun et al.[7]the system update rules were more similar to the CA model,in which it needed to check each cells whether occupied or not when updating system.Thus,the computational efficiency was relatively low.Meanwhile,the DTM proposed by Yang et al.[6]was incapable of simulating heterogeneous train traffic flow.To remedy these defects of the two kinds of simulation models mentioned above,we develop the discrete-time model with four train control strategies to simulate the high-speed railway traffic flow.In the improved discrete-time model,the space is continuous and the time is discrete,so that the computational efficiency is higher.However,we focus on investigating the characteristics of heterogeneous high-speed train traffic flow without considering the energy consumption and train failure in present work.
The rest of the paper is organized as follows.In Sec.2,the basic principles of the moving block system(MBS)are introduced and an improved discrete-time model to simulate heterogeneous high-speed passenger train traffic flow under MBS is proposed.In Sec.3,the simulation results,analysis and discussions are presented.Finally,the main work of this research is summarized in the Conclusion.
2 Model for Heterogeneous High-Speed Train Traffic Flow
2.1 The Theory of Moving Block System
To ensure the safety of train operation in the railway network,there are three types of signal system,i.e., fixed block system(FBS),quasi-moving block system(QMBS),and moving block system(MBS).With FBS,the track segment between stations is divided into a series of block sections,which can handle at most one train at a time.The typical FBS is three-aspects,i.e.,red,yellow,green wayside signals,which control train traffic on the routes and impose safe space distance headway between trains.A train is permitted to enter the next block section if the signal aspect is either green or yellow,while if the signal aspect remains red,the train is required to decelerate and stop before the next block section,which called overlap protection block sections.In contrast,the QMBS is not regulated by signal lights and the tracking target of following train is the end of the block section,which is occupied by its preceding train.But generally speaking,there are some overlap protection block sections to ensure safe operation in both FBS and QMBS.
Unlike FBS and QMBS,it is no need to divide the railway line into separate block sections in MBS.As shown in Fig.1,train i,where i∈[1,N?1]is the real-time order of trains on the railway line at time t and N is the number of trains in simulation system,can continuously communicate with its preceding train i?1 to obtain the real-time exact position,velocity,travel direction and other relative information of train i?1.According to real-time information,the control center calculates the minimum safe distance dmin?i(t),the real-time headway distance Hi(t),and the empty space to its preceding station gapi(t)at time t.Then,the operation of train i in the next time step t+?t is determined by comparing these parameters.Without overlap protection block sections,the tracking safe distance in MBS is obviously shorter than that in FBS and QMBS.Thus,it can obviously enhance the transport capacity of the railway line.As a matter of the fact,MBS has been applied extensively in Chinese high-speed railway system and the subway system.With the development of communication techniques,more and more railway lines would be equipped with MBS.
Several moving-block schemes have been discussed so far,[17]including moving space block(MSB),moving time block(MTB)and pure moving block(PMB).The equations of the minimum safe distance are diverse with different schemes and have been discussed in detail in Ref.[5].Xu et al.[5]have found that considering the velocity effect of preceding train can reduce the minimum safe distance and enhance the traffic capacity of railway line.So,taking the length of train and velocity effect of preceding train into account,we extend the minimum safe headway formulation between train i and train i?1 as the following:

where vi(t)and vi?1(t)are the velocity of focal train i and preceding train i? 1 at time t respectively;Ltraini?1is the length of preceding train i?1;SM is the safety margin space;agbis general deceleration rate of train i and aebis the emergent deceleration rate of train i?1.
Moreover,the exact train position Xiis the head of train i in this paper.Since the space in the simulation model is continuous and the acceleration/deceleration rate is not an integer,trains may not pull in at the accurate position of station.Thus,the position deviation of trains stop at station ranges in[?0.5,0.5]is considered acceptable in this paper.Consequently,the real-time headway distance Hi(t)and the empty space to its preceding station gapi(t)are computed by the following formulation:
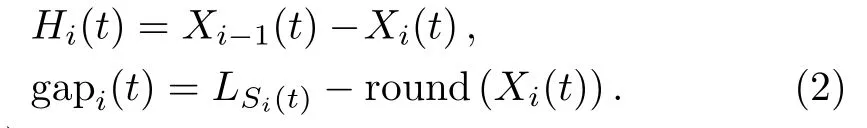
where Si(t)is current stop station or approaching station of train i,LSi(t)is the position of current stop station or the approaching station of train i at time t and round(x)rounds the elements of x to the nearest integers.If gapi(t)=0,it implies that train i is dwell at station Si(t)at time t.
2.2 An Improved Discrete-Model with effective Travel Control Strategies
In the discrete-time model present in Ref.[6],the train traffic is homogenous without considering the overtaking operation.So,an improved discrete-time model is proposed to simulate the heterogeneous high-speed train traffic flow on double-track railway line in this paper.The underlying dynamics of the improved discrete-time model are regulated in the train control strategies,which are utilized to determine appropriate operation employed in train movements at every time step.Before presenting our simulation approach,some assumptions are made as follows:
(i)All the trains are running on a double-track line and we only consider unidirectional train traffic.
(ii)The route of each train is fixed.It means that the departure station and the destination station are fixed.
(iii)The number of platforms in each station is limited.If the platforms are all occupied by trains,the following should wait outside.In addition,all the trains should dwell at least 2 minutes at each station.
(iv)There are 2 types of train with different maximum velocities.The fast train can and only can overtake the slow train at an intermediate station.
(v)In the simulation,a train with zero velocity will appear at original station after every departure time intervals.When train i arrives at its destination,it disappears,i.e.,Xi=null and will not be considered any more.
(vi)The minimum safe distance of adjacent train is not a constant but a computed value based on real-time information.
(vii)The railway line is always normal during the simulation process,i.e.,without considering the disruption.
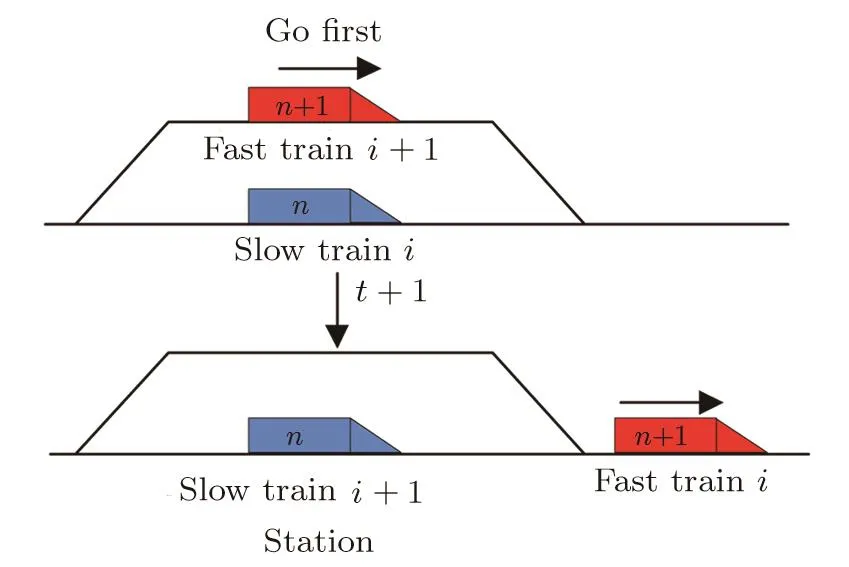
Assume that there are N trains,which are running on the railway line toward the same direction.These trains are numbered in departure order at the original station,denoted by the permanent labels 1,2,3,...,n?1,n,n+1,...,N,which remain unchanged during the whole trip of trains.While,the order of trains may change when the overtaking operation occurs,thus the real-time order of trains on the railway line is denoted by the temporary labels 1,2,3,...,i?1,i,i+1,...,N.As depicted in Fig.1,train i?1,i,i+1 represent the real-time order on the railway line and n+1,n?1,n labeled on the train denote the departure order of these trains.
In order to present the improved discrete-time movement model clearly,some symbols and parameters are presented in Table 1.

Table 1 Subscripts and parameters employed in the paper.

Fig.1 (Color online)Diagram of trains in the simulation system.
2.2.1.effective Train Control Strategies
The train movements are influenced by many uncertain factors in the process of operation.effective train control strategies can guarantee the security of train operation and obtain the efficient train timetable.Therefore,accurate train control strategies are the foundation and key technology for train operation.In the improved discrete-time model,the effective train control strategies are designed as follows:
(i)Departing Strategy
If the focal train i is a slow train,it has to remain at the station when the one of following cases occurs:
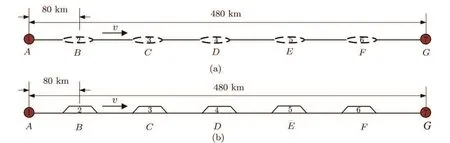
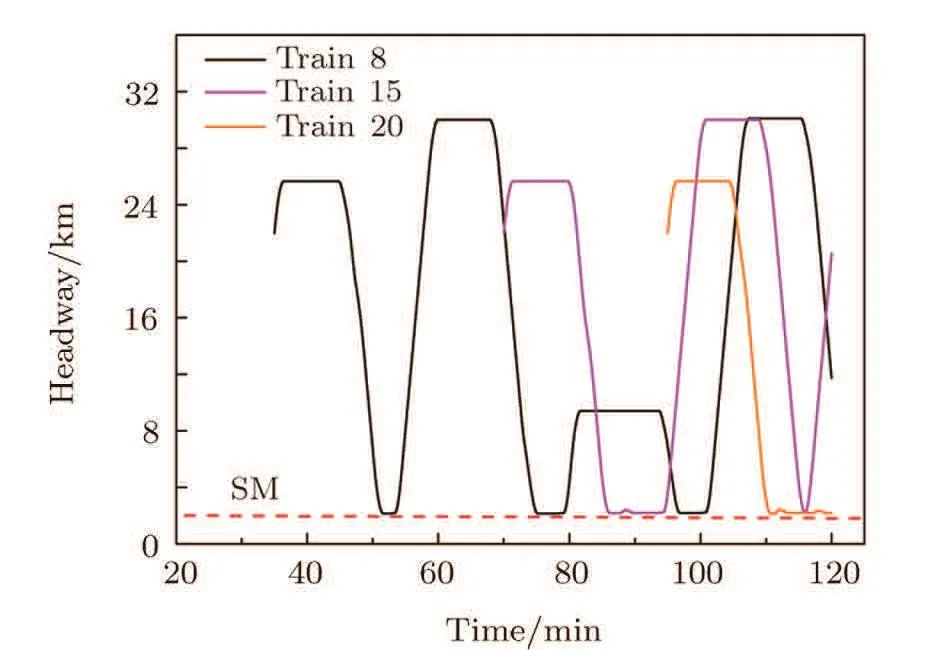
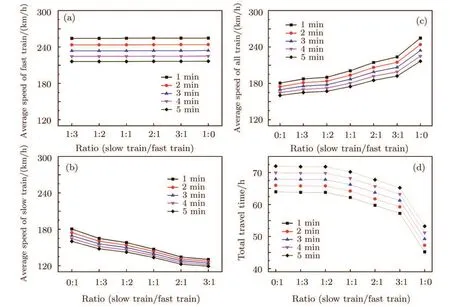
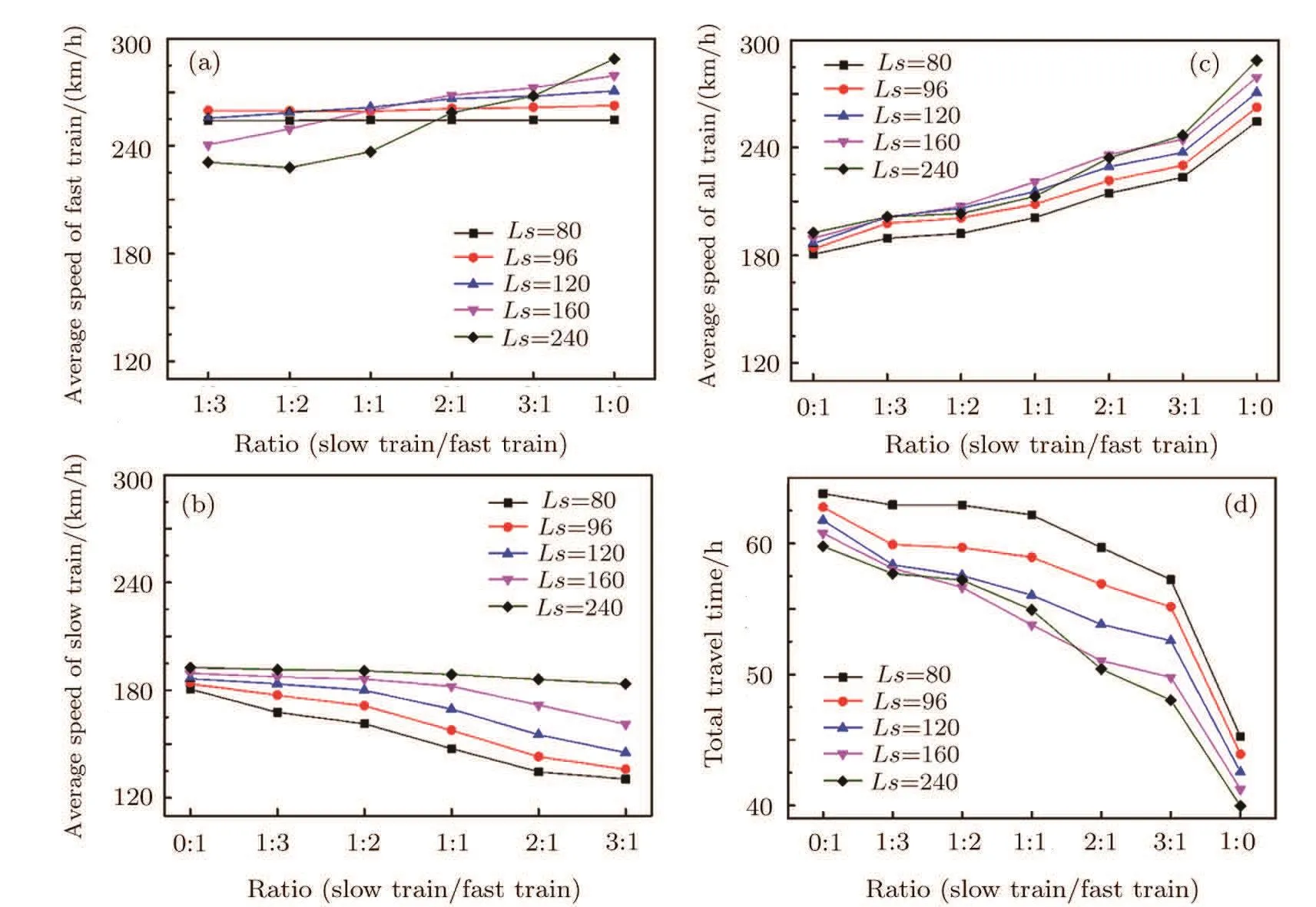
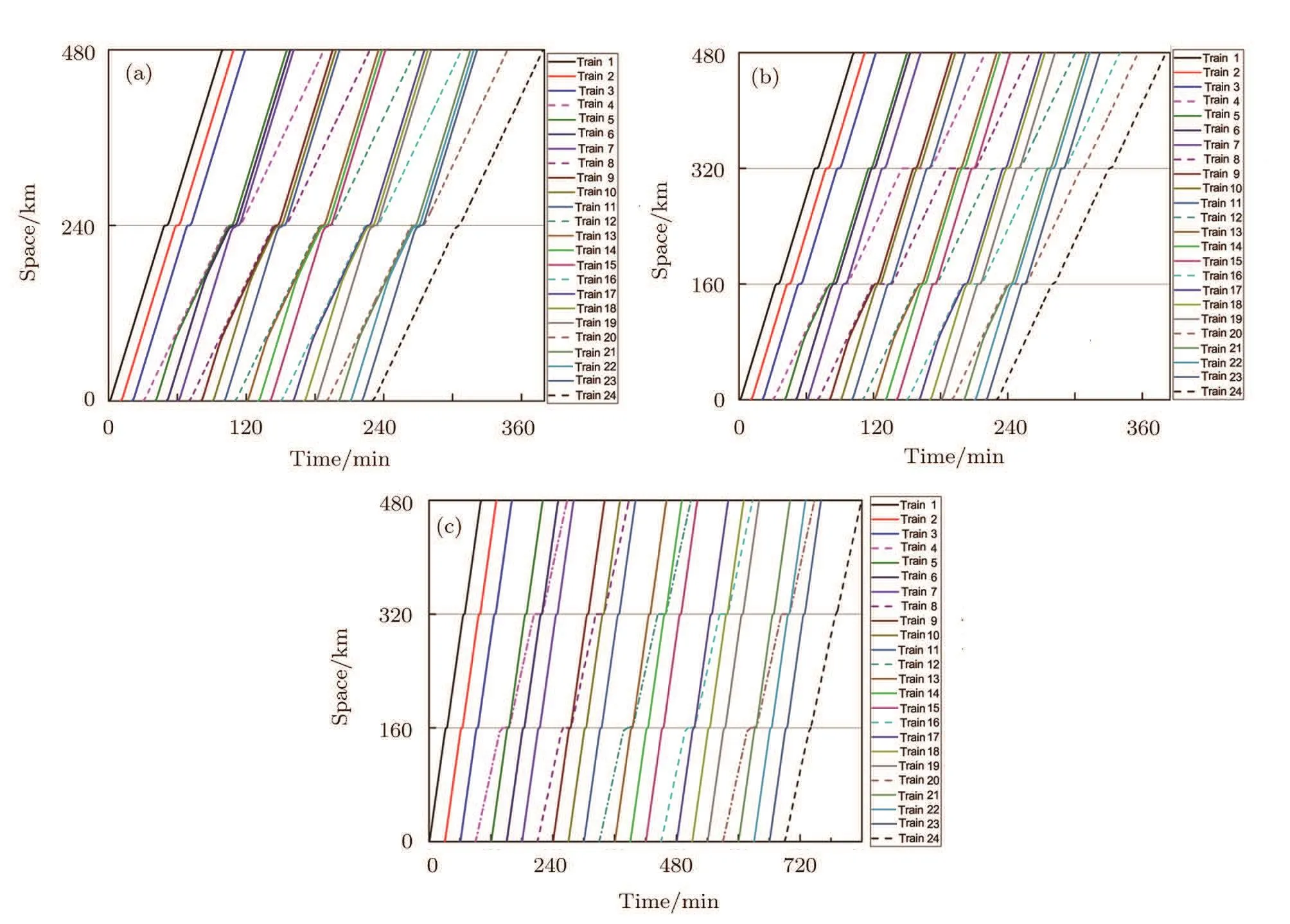
(a)The dwell time of train i is shorter than the fixed dwell time,i.e.,DTi?Si(t) (b)The dwell time of train i is longer than the fixed dwell time,but the headway distance is shorter than the minimal safe distance,i.e.,DTi?Si(t)>DTfixand Hi(t)6 dmin?i(t); (c)Train i has dwelled for enough time and the headway distance is longer than the minimal safe distance,i.e.,DTi?Si(t)>DTfixand Hi(t)>dmin?i(t),but its following train i+1 is a fast train with higher priority,we use overtaking strategy to determine whether it should remain at the station to wait for being overtaken or not. If train i is a fast train,it has to remain at the station only when case(a)or case(b)occurs,i.e.,the fast train i is no need to wait for being overtaken.In addition,the new train,created at the origin station after every departure time intervals,can be regarded as the train that has dwelled enough time and waits for departing. Thus,if train i remains at station,its status is updated according to the following formulation: Otherwise,train i can travel forward to next section,its status is updated according to the following formulation: (ii)Traveling Strategy If train i is running in a certain section and far from its preceding station(gapi(t)>Sib)and its preceding train i? 1(Hi(t)>dmin?i(t)),then it would travel with acceleration or maintain its maximum velocity,and accordingly its status is updated according to the following formulation: (iii)Braking Strategy If train i is running behind train i?1 in the same section or prepares to pull in its preceding station,it has to brake when Hi(t)6 dmin?i(t)or gapi(t)6 Sib,i.e.,the headway distance between train i and train i?1 is shorter than the minimal distance or the empty space to preceding station is less than general braking distance of train i.Then,the status of train i is updated by the following formulation: Significantly,the specific real-time deceleration rate of train i?1 is determined by Algorithm 1 which will be given in Subsec.2.2.2. (iv)Overtaking Strategy When train i with a lower priority has just dwelled for enough time and a faster train i+1 is running behind,it remains at the station to wait for being overtaken if and only if ti>ti+1,where ti(ti+1)represents the travel time for train i(i+1)arriving at next station,calculated according to the following formulation: where tfi(tf(i+1))represents the free running time for train i(train i+1)to next station,Sibare the general braking distance for train i with maximum velocity. Obviously,the overtaking strategy is simpler and more efficient than that mentioned in Ref.[7].Significantly,as illustrated in Fig.2,the real-time order of trains would be changed when overtaking operation is completed,i.e.,the fast train n+1 dwells for fixed dwell time and then departs earlier than slow train n.Then,the former following train n+1 becomes the leading train of train n after completing overtaking.Accordingly,train n+1 is labeled by train i and train n is labeled by train i+1 after completing overtaking. Fig.2 (Color online)Diagram of overtaking operation at intermediate station. Generally,there are five relative operations when train traverses each section,i.e.,departing operation,traveling operation,braking operation,dwelling operation at stations and overtaking operation.To sum up,at time t,the operation of the focal train i is determined by the following rules: (a)If train i is at the origin station or dwelling at an intermediate station,adopt departing strategy to determine whether depart or not,i.e.,execute departing operation or dwelling operation. (b)If train i is far from its preceding station and its preceding train i?1,the travelling operation is employed. (c)If train i can pull in its preceding station or its actual headway is shorter than the minimum safe headway,the braking operation is employed. (d)If train i is a slow train with a lower priority than train i+1,the overtaking strategy is adopted to determine whether train i needs to wait for being overtaken or not. 2.2.2.The Improved Discrete-Model In this paper,the underlying dynamics of the proposed simulation model is governed by the above four control strategies,which are utilized to determine appropriate operation employed in train movements at every time step.In addition,as mentioned in Subsec.2.2.1,in traveling and braking operation,the acceleration rate of train may vary.Thus,before presenting the improved discrete-time model with effective train control strategy,we may firstly investigate the variation of train acceleration rate. In practice,considering passengers’comfort and operation safety,the maximum starting acceleration rate of high-speed train is 0.6 m/s2and the average acceleration rate is 0.5 m/s2;the average deceleration rate is 0.75 m/s2and emergent deceleration rate is 1.5 m/s2.[18]Yet,these characteristics are not taken into account in Ref.[7].Thus,to reflect the reality,the general traction acceleration/deceleration rate are assumed as a constant in this paper,i.e.,aga=0.5 m/s2,agb=?0.75 m/s2and aeb=?1.5 m/s2.Combining with specific condition in the train movements on the railway line,we utilize the following Algorithm 1 to determine ai(t). Algorithm 1 Step 1Calculating the real-time dmin?i(t)according to Eq.(1)and Hi(t),gapi(t)according to Eq.(2),separately.Step 2Detecting the location of train i.If Hi(t)=gapi(t),go to step 3;else if Hi(t) Step 3If Xi?2(t)=Xi?2(t),the preceding station of train i is occupied by two train,go to step 4;else train i can pull in station,go to step 5. Step 4If Hi(t)>dmin?i(t),train i executes traveling operation,go to step 6;else,train i executes braking operation and ai(t)=min(agb,?vi(t)2/2(Hi(t)? Ltraini?1)).Step 5If Sib< gapi(t),train i executes traveling operation,go to step 6;else if Sib>gapi(t)and vi(t)2/2agb Step 6If vi(t)+aga·△t 6 Vi?max,ai(t)=aga;else ai(t)=(Vi?max? vi(t))/?t. As described in Step 5 of Algorithm 1,we can see that the braking rules can guarantee train approaching smoothly to its preceding station without stopping outside of station.Hence,with the real-time calculated acceleration of every train,the improved discrete-time model can be formulated as follows: where t,t+?t∈[0,T],i∈[1,N?1]and T is the total simulation time.Therefore,based on the above control strategies,we have designed Algorithm 2 to realize the improved discrete-time model. Algorithm 2 Step 1 InitializationSet t= 0,N = 0,and DTi?Si(t)(t)=0. Step 2Depart new train and clean out train. Step 2.1If t/Tint=round(t/Tint),N=N+1,vN=0,XN=0,Si(t)=1,go to Step 2.2. Step 2.2For i:=N,if Xi>L,train i departs from simulation system,Xi=null,go to step 3. Step 3Calculate necessary foundation data.For i:=N,if Xi6=null,calculate dmin?i(t)according Eq.(1),calculate Hi(t),gapi(t)according to Eq.(2),go to step 4. Step 4Determine the appropriate operation for every train. Step 4.1Set i=1. Step 4.2If gapi(t)=0,train i is at station,go to step 4.3,else go to step 4.6. Step 4.3If DTi?Si(t)(t) Step 4.4If train i is a slow train and its following train i+1 is a fast train,calculate and according to Eq.(7),go to step 4.5,else Si(t)=Si(t)+1,gapi(t)=LSi(t)?round(Xi(t)),go to step 4.6. Step 4.5If ti>ti+1,train i remains at the station to wait for being overtaken,opi(t)=2,go to step 4.7;else,Si(t)=Si(t)+1,gapi(t)=LSi(t)?round(Xi(t)),go to step 4.6. Step 4.6If Hi(t)> gapi(t),opi(t)= 1;else if Hi(t)=gapi(t)and Xi?2(t)6=Xi?1(t),opi(t)=1;else if Hi(t)=gapi(t)and Xi?2(t)=Xi?1(t),opi(t)=0;else if Hi(t) Step 4.7If i Step 5Update the status of each train. Step 5.1Set i=1. Step 5.2If opi(t)=2,go to step 5.3;else if opi(t)=1,go to step 5.4;else if opi(t)=0,go to step 5.5. Step 5.3Train i is dwelling at station. Calculate Xi(t+?t),vi(t+?t),according to Eq.(3),go to step 5.6.Step 5.4Train i is running behind a station.If gapi(t)>dmin?i(t),train i performs traveling operation,and calculate Xi(t+?t),vi(t+?t)according to Eq.(5);else,calculate Xi(t+?t),vi(t+?t)according to Eq.(6).Then,go to step 5.6. Step 5.5Train i is running behind a train.If Hi(t)>dmin?i(t),train i performs traveling operation,and calculate Xi(t+?t),vi(t+?t)according to Eq.(5);else,calculate Xi(t+?t),vi(t+?t)according to Eq.(6).Then,go to step 5.6. Step 5.6If i Step 6If t To demonstrate the effectiveness and efficiency of the simulation model proposed above,some numerical experiments are carried out in this section.In the simulation system,the double-track railway line consists of 7 stations,including 2 terminal stations,denoted by A,G and 5 intermediate stations,denoted by B,C,D,E,and F.For simulating homogeneous train traffic flow,all intermediate stations can only be occupied by one train at same time(see Fig.3(a)).On the other hand,the intermediate stations allow two trains to dwell simultaneously to complete overtaking operation(see Fig.3(b))for simulating heterogeneous train traffic flow.In all experiments,the terminal stations have multiple platforms,where trains can originate and terminate.The railway line includes 6 sections,denoted by AB,BC,CD,DE,EF,and FG,and the length of each section is 80 km.In addition,the position of terminal station A is 0 m;the increment of discrete time is set as 1 s,i.e.?t=1 s.The length of all the trains are set as Ltrain=200 m.All the experiments are performed on an Intel(R)Core(TM)i3-2130 with 3.40 GHz CPU and 4.00 GB memory,and all the algorithms are implemented in Microsoft Visual Studio 2010 C#on the Windows 7 platform. Firstly,we verify the correctness and efficiency by simulating homogeneous train traffic flow on the tested railway line where the station has only one platform(see Fig.3(a)). There are 20 trains to traverse the tested railway line where the maximum velocity of trains vmax=306 km/h=85 m/s,the departure time intervals at original station Tmin=5 min,the fixed dwell time DTfix=4 min for passengers getting on/off trains,and the safety margin space SM=2.0 km. Figure 4 demonstrates the space-time diagrams of three pair adjacent trains,including train 7 and train 8,train 14 and train 15,train 19 and train 20.From Fig.4,we can see that each train dwells at each intermediate station for 2 min and then departs.The following trains need to wait outside when its preceding train is dwelling at its preceding station,for instance,when t=7141,the train 19 is dwelling at the intermediate station B with X19=80 km and the train 20 is stopping outside with X20=77.8055 km.It also can be found from Fig.4 that even the following trains are very close to their preceding trains,the actual headway distance always exceeds the safety margin space SM,as illustrated in Fig.5.In order to verify the efficiency of the proposed simulation approach,we use the last train,i.e.,train 20 arrivals at its destination station as the simulation program termination condition.The CPU time is 1.35 s,which is obviously faster than the discrete-event model(DEM)mentioned in Ref.[13],where the CPU time is approximately 3.81 s when there are only 15 trains running on its tested railway line with 60 km.It suggests that the simulation approach based on the proposed improved discrete-time model is effective and efficient. Then,with the proposed simulation approach,the heterogeneous train traffic flow is tested on railway line in Fig.3(b).Two types of trains are taken into account,including fast trains with maximum velocity Vf?max=306 km/h=85 m/s and slow trains with maximum velocity Vs?max=198 km/h=55 m/s.According to the service requirements,fast train and slow train are scheduled to depart from their origin in turn,and the number of two types of departure train is determined by the ratio r,which indicating fast trains to slow trains.For instance,if r=1:2,it means a fast train and two slow trains depart in succession. Fig.3 (Color online)Diagrams of the railway line in experiments:(a)railway line for simulating homogeneous train traffic flow,(b)railway line for simulating heterogeneous train traffic flow. Fig.4 The space-time plot of homogeneous train traffic flow. Fig.5 (Color online)The headway of different trains at different time. Fig.6 (Color online)The space-time plot of heterogeneous train traffic flow,where r=1:1,SM=2.0 km,DT fi x=2 min,(a)Tint=8 min,(b)Tint=10 min. Figure 6 indicates the heterogeneous train traffic flow with different departure time intervals,where the solid lines indicate the fast trains;the dashed indicate the slow trains.From Fig.6,we can see that the fast trains would overtake the slow trains at a certain intermediate station at appropriate time,for instance,in Fig.6(b),the fast train 3 overtakes the its front slow train 2 at station B at simulation time t=2406. In this paper,the traffic capacity of the tested railway line in Fig.3(b)is defined as the number of train arrives at its destination within a given simulation time,i.e.,T=24000.In this subsection,we mainly investigate the influences of departure time intervals Tint, fixed dwell time DTfixand the ratio of fast trains to slow trains r on traffic capacity of the tested rail line. Figure 7 indicates the traffic capacity of the railway line varying with different departure time intervals and fixed dwell time.As shown in Fig.7(a),the shorter the departure time intervals is,the larger the traffic capacity is,since the shorter departure time intervals allows more trains running on the railway line.For instance,combined with Fig.6,the number of trains running on the railway line is 25 when Tint=8 min and that turns to 20 when Tint=10 min within 12000 simulation times.Although the shorter departure time intervals lead to higher density,it also may cause more train delays and thus increase the total travel time of relative trains.It can be easily seen in Fig.6 that the slow trains are delayed by fast trains for overtaking operation,e.g.the slow train 2 is overtaken by fast train 1,train 3,train 5,train 7 and arrives at destination at t=11237 when Tint=10 min,but it is overtaken by additional other two trains,i.e.,train 9,train 11 and arrives at destination at t=12534 when Tint=8 min.Thus,the more delay caused by fast trains to slow train 2 is 1207.Furthermore,as shown in Fig.7(b),the shorter the fixed dwell time is,the larger the traffic capacity is.The reason is that the shorter dwell time would reduce the total travel time for all trains traversing the railway line and result in more train arriving destination within a given simulation time. Furthermore,it can be easily found from Fig.7 that the traffic capacity increases with the increment of the ratio of fast trains with a certain departure interval.The reason is that faster trains with less travel time can arrive at destination within given time.Besides,under the same situation conditions,the traffic capacity with whole fast trains is obviously more than that with whole slow trains,for instance,the traffic capacity is 27 with r=1:0 and it is 22 with r=0:1 when DTfix=6 min,as shown in Fig.7(b).Obviously,the simulation results are consistent with the actual rail traffic situation. The average velocity of trains is defined as the total velocity divided by the total number of train N,i.e.,In our simulation experiments,we have investigated average velocity of 24 trains.In this subsection,we mainly investigate the influences of fixed dwell time DTfix,departure time intervals Tint,section length and the ratio of fast trains to slow trains on the average velocity of train. Figure 8 indicates the average velocity of trains varying with fixed dwell time when Tint=10 min,SM=2.0 km.As shown in Figs.8(a)–8(c),the average velocity of fast trains,slow trains,and all the trains decrease with the increment of fixed dwell time.The reason is that increasing the fixed dwell time leads to increment of total travel time for every train,naturally the average velocity decreases.Meanwhile,it is clearly that average velocity of fast trains hardly fluctuate when the ratio r varies(see Fig.8(a)),while the average velocity of slow trains are downtrend(see Fig.8(b))and the average velocity of all the trains increases with increment of ratio(see Fig.8(c)).The reason is that all fast trains can overtake their front slow train at a certain intermediate station and keep moving on with finitely influenced by slow trains.Contrarily,slow trains may be delayed by fast train when overtaking operation taking place.At the same time,fewer fast trains running on the railway line may cause fewer overtaking operation occurs,resulting in less extended dwell time of slow trains at intermediate station.Thus,the average velocity of slow trains with smaller ratio is faster.In addition,the total travel times increase with the increment of fixed dwell time,but with a certain fixed dwell time,the decline of total travel time is not significant when r<1 and dropped markedly when r>1,as shown in Fig.8(d).It is because that the average velocity of all trains increases for the incensement the ratio of fast trains,despite the average velocity of slow trains falls.Thus,there is little change in total travel time when r<1. Fig.8 (Color online)Average velocity of trains varying with fixed dwell time,where(a)is of the fast trains,(b)is of the slow trains,(c)is of all the trains,and(d)is the total travel time of all the trains. Subsequently,we investigate the simultaneous influence of section length and departure time intervals on the average velocity of trains.It is worthwhile to note that the length of section,presented by Ls,is changed by setting different number of intermediate station,and the total length of the testes railway line is still 480 km.Figures 9 and 10 indicate the three different types of train average velocity and total travel time of train varying with different length of section when Tint=10 min and Tint=30 min,respectively,where DTfix=1 min,SM=2.0 km. Combining with Figs.9 and 10,we can see that average velocity of fast trains in Fig.9(a)vary more complicatedly than that in Fig.10(a).In order to interpret the complicated phenomenon clearly,we have the aid of the diagrams of Space-Time of all the 24 trains shown in Fig.11.From Figs.11(a)–11(b),we can easily see that the fast trains are hindered by their front trains when Tint=10 min,while the fast trains would not be delayed by any trains and run freely when Tint=30 min,as shown in Fig.11(c).Besides,as illustrated in Fig.11(a),some fast trains may not only be delayed by their front slow train but also some front fast trains when Ls=240 km.For instance,the delays of train 5,caused by train 4 running on the same section,may propagate backward to train 6 and train 7.On the contrary,as illustrated in Fig.11(b),train 6 and train 7 would not be delayed by train 5 when Ls=160 km,because that the slow train 4 has been dwelling at preceding station to wait for being overtaken since the section length is shorter.Thus,the average velocity of fast trains when Ls=240 km is slower than that with Ls=160 km,which is in keeping with Fig.9(a). Furthermore,the influence of the ratio of fast trains to slow trains on trains’average velocity is discussed.Comparing Fig.9(a)with Fig.10(a),we can see that the average velocity of fast trains increases with the increment of section length but hardly invariant with a certain section length in Fig.10(a).The main reasons are as follows:(a)Long section length means reducing the number of intermediate station,thus the acceleration/deceleration operations and the total fixed dwell time at intermediate station all reduce;(b)No matter how many slow trains in system,all the fast trains would not be hindered by them and can run freely on the railway line when the departure time intervals is large enough,for instance,Tint=30 min.Comparing the results in Fig.10 with that in Fig.9,we can notice that the average velocity of slow trains are relatively faster in Fig.9(b)than that in Fig.10(b).It implies that the delay of slow trains raised by fast trains is heavier with larger departure time intervals.It may be that the slow trains often need to dwell extended time to wait for being overtaken by its following fast trains.While,the average velocity of slow trains all generally falls with decrement of section length. Fig.9 (Color online)Average velocity of trains varying with length of sections when Tint=10 min,where(a)is of the fast trains,(b)is of the slow trains,(c)is of all the trains,and(d)is the total travel times. Fig.1 0 (Color online)Average velocity of trains varying with length of sections when Tint=30 min,where(a)is of the fast trains,(b)is of the slow trains,(c)is of all the trains,and(d)is the total travel times. Fig.1 1(Color online)The heterogeneous train traffic flow,where r=3:1,SM=2.0 km and(a)Tint=10 min,Ls=240 km,(b)Tint=10 min,Ls=160 km,(c)Tint=30 min,Ls=160 km. To sum up,we could conclude that the average velocity of trains is not only related to fixed dwell time,the ratio of fast trains to slow trains,the section length but also the departure time intervals.For instance,the average velocity of fast trains is 279 km/h when Tint=30 min,Ls=160 km,r=3:1,and it is 272 km/h when Tint=10 min,Ls=160 km,r=3:1,and it is 268 km/h when Tint=10 min,Ls=240 km,r=3:1.Thus,in order to guarantee railway traffic service quality and efficient operation,the railway operation departments should adopt a suitable departure time intervals and train stop scheme to balance the traffic capacity against train delays. In this paper,we propose an improved discrete-time model with four effective control strategies to simulate heterogenous train movements on high-speed railway.Additionally,a new efficient algorithm is designed to realize our simulation approach.With the proposed simulation approach,some major characteristics of train traffic can be well captured. With the proposed simulation model,we have analyzed the traffic capacity and train average velocity with different departure time intervals, fixed dwell time,the section length,the ratio of fast trains to slow trains,etc.The simulation results indicate that smaller departure time intervals can increase the traffic capacity but may bring out more train delays,leading to the slowing down of the average velocity. Meanwhile,a longer section length and greater ratio of fast trains also have positive influence on traffic capacity and train average velocity.The shorter fixed dwell time can also increase traffic capacity and train average velocity.Thus,railway operators can improve the work efficiency at the intermediate station to guarantee railway transportation service quality.Furthermore,the railway operation departments should adopt a suitable departure time intervals and train stop scheme to balance the traffic capacity against train delays. Furthermore,in the daily train operation,the train movement becomes more complex when some unexpected event occurs,for instance,train failure,track failure.So,in the further work,we can take the energy consumption,emergency and other related factors into account to optimize the train movement in railway system. References [1]K.Li,Z.Gao,and B.Ning,J.Comput.Phys.209(2005)179. [2]K.Li,Z.Gao,and B.Ning,Int.J.Modern Phys.C 16(2005)921. [3]H.Zhou,Z.Gao,and K.Li,Acta Phys.Sin.55(2005)1706. [4]Y.Fu,Z.Gao,and K.Li,J.Tran.Sys.Eng.&Info.Tech.8(2008)89. [5]Y.Xu,C.Cao,M.Li,and J.Luo,Commun.Theor.Phys.58(2012)847. [6]L.Yang,F.Li,Z.Gao,and K.Li,Chin.Phys.B 19(2010)100510. [7]Y.Sun,C.Cao,Y.Xu,and C.Wu,Chin.Phys.B 22(2013)120501. [8]M.Dorfman and J.Medanic,Transp.Res.Pt.BMetholdol.38(2013)81. [9]F.Li,Z.Gao,K.Li,and L.Yang,Transp.Res.Pt.BMetholdol.42(2013)1008. [10]X.Xu,K.Li,L.Yang,and J.Ye,Appl.Math.Model.38(2014)894. [11]T.Tang,H.Huang,and G.Xu,Physica A 387(2008)6845. [12]T.Tang,H.Huang,S.Wong,and R.Jiang,Chin.Phys.B 18(2009)975. [13]S.Zhang and Y.Chen,Physica A 390(2011)3710. [14]L.Yang,K.Li,Z.Gao,and X.Li,Omega-Int.J.Manage.Sci.40(2012)619. [15]J.Ye and K.Li,Chin.Phys.B 22(2012)050205. [16]X.Xu,K.Li,and L.Yang,Chin.Phys.B 23(2013)08020. [17]L.V.Pearson,Moving-block Signaling,(Ph.D.Thesis)Lough borough University of Technology(1973). [18]http://bbs.railcn.net/thread-1043683-1-1.html.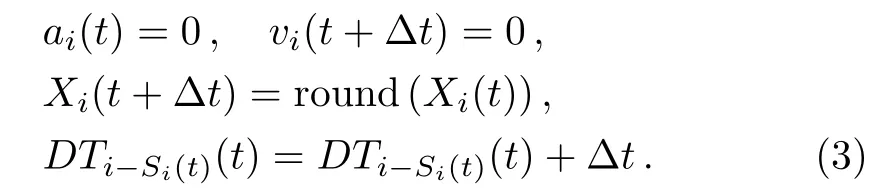
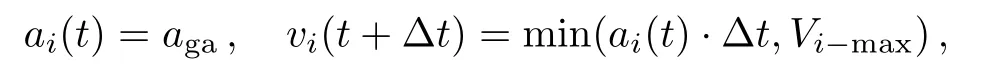
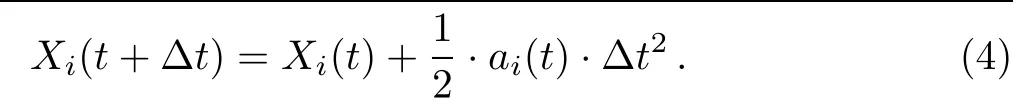
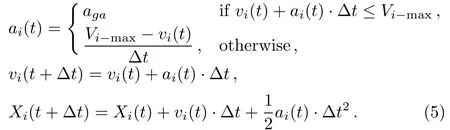
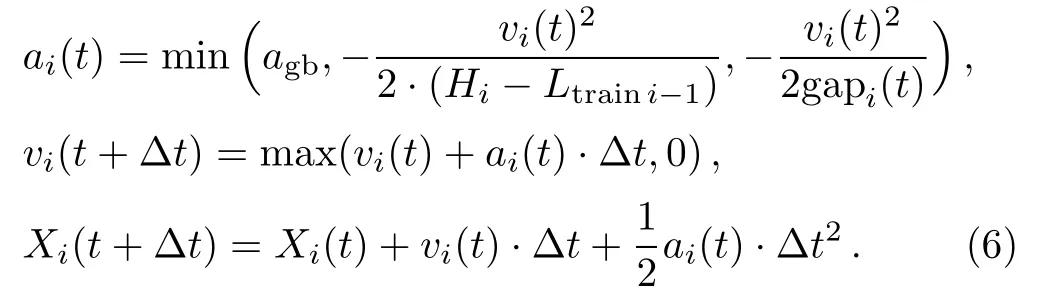
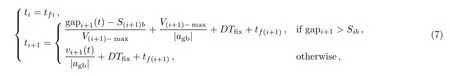
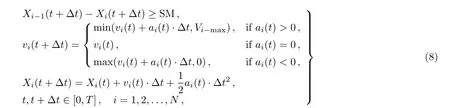

3 Numerical Simulations
3.1 The Simulation Experiments


3.2 The Traffic Capacity Analysis
3.3 The Average Velocity Analysis
4 Conclusions
 Communications in Theoretical Physics2016年3期
Communications in Theoretical Physics2016年3期
