xF3(x,Q2)Structure Function and Gross-Llewellyn Smith Sum Rule with Nuclear E ff ect and Higher Twist Correction?
N.M.Nath,A.Mukharjee,M.K.Das,and J.K.Sarma
1Department of Physics,Rajiv Gandhi University,Rono Hills,Doimukh-791112,Arunachal pradesh,India
2High Energy Physics Laboratory,Department of Physics,Tezpur University,Tezpur-784028,Assam,India
1 Introduction
Proper understanding of the DIS(deep inelastic scattering)structure of nucleon and associated sum rules is expected to o ff er an important opportunity to investigate Quantum Chromodynamics(QCD)as a theory of strong interaction and hence these are regarded as the objects of intensive investigation both theoretically and experimentally in recent years(see for example Ref.[1]and references therein).With the recent developments of dedicated experimental facilities significant progresses have been observed in the field of experimental investigation of structure functions.Simultaneously,in this regard,tremendous progress is observed in the field of theoretical investigation with a variety of theoretical approaches.
Quantum Chromodynamics(QCD)is one of the most important theoretical approaches in order to account for the strong interaction processes observed at high energy particle colliders. However,the predictive power of QCD is limited. QCD is successful in describing Q2dependency of the structure functions in accord with DGLAP(Dokshitzer–Gribov–Lipatov–Altarelli–Parisi)evolution equations[2]in the perturbative regime i.e.,within the Bjorken limit(Q2?1,x fixed and not too small).However the most important region in DIS,which has attracted much interest recently is the small-x region,lies between the interface of Bjorken limit and the Regge limit.
The DGLAP equation is a renormalisation group equation for the quarks and gluon inside hadron.It is one of the fundamental equations of perturbative quantum chromodynamics(pQCD),being central to all theoretical predictions for lepton-hadron colliders.Solutions of DGLAP equations give the Q2evolution of both the parton distribution functions as well as various structure functions.Although QCD predicts the Q2dependence of structure functions in accord with the DGLAP equations but they have limitations on absolute prediction of structure functions.DGLAP equations cannot predict the initial values from which the evolution starts,they can only predict the evolution of structure functions with Q2,once an initial distribution is given.Further,due to its complicated mathematical structure,an exact analytic determination of the structure functions is currently out of reach and one needs to apply approximated methods to arrive on predictions from the DGLAP equation.Accordingly several approximate numerical as well as semi-analytical methods for the solution of DGLAP equation have been discussed considerably over the past years(see Refs.[3–8]and references therein).
In our previous paper Ref.[8],the small-x behaviour of xF3(x,Q2)structure function and the GLS sum rule was obtained by means of solving the DGLAP evolution equation using a Q2dependent Regge behaved ansatz as initial input with pQCD corrections upto next-next-to-leading order(NNLO).In accord with Ref.[8]the solutions,governing the small-x behaviour of xF3(x,Q2)structure function in LO,NLO,and NNLO are given by
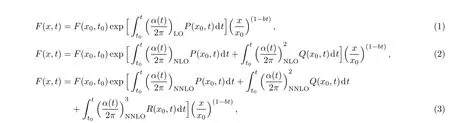
respectively,where the structure function xF3(x,t)is denoted by F(x,t)for nothing but simplicity,where t=ln(Q2/Λ2)and Λ is the QCD cut o ffparameter.Here

in which the two loop and three loop correction terms to the splitting functions for non-singlet structure functions are given by[9]
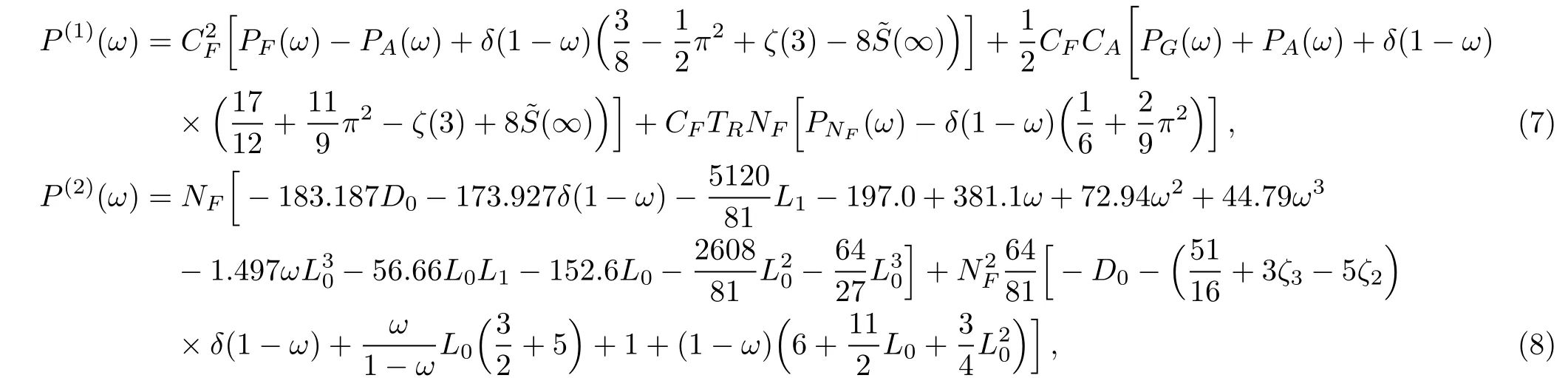
with
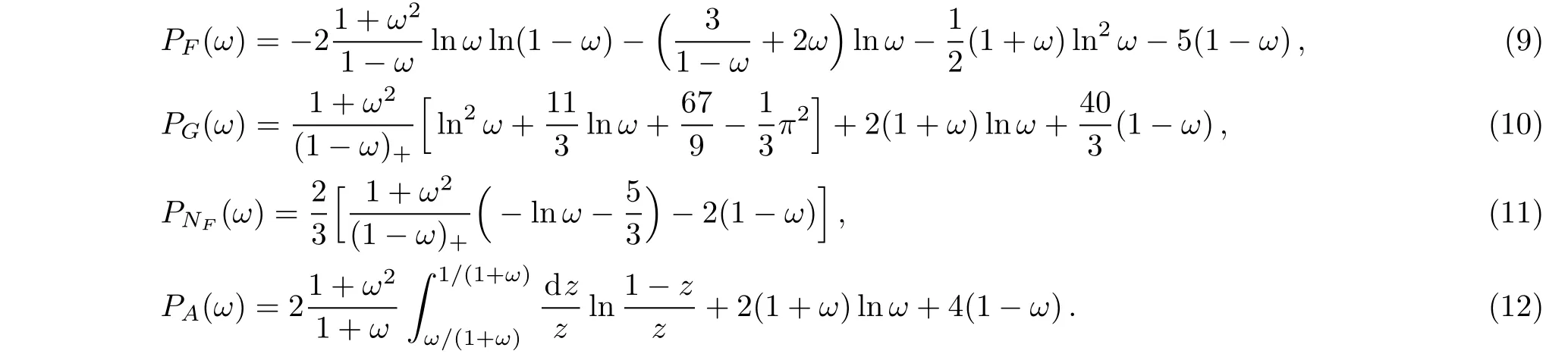
Here the following abbreviations are used,

The results for small-x behaviour of structure function in accord with Eqs.(1),(2),and(3)were observed to be consistent with the available experimental data taken from CCFR,[10?11]NuTeV,[12]CHORUS,[13]and CDHSW[14]collaborations as well as with several other strong analysis performed by MRST98,[15]CTEQ4,[16]KPS,[17]and KS[18]for xF3(x,Q2)structure functions.The phenomenological success achieved in this regard inspired us to utilise these results in determining the GLS sum rule,which is associated with xF3(x,Q2)structure function.
Considering above relations for the small-x behaviour of xF3(x,Q2)structure function we obtained the GLS integral with LO,NLO,and NNLO corrections as respectively and they were also observed to be compatible with the CCFR[11]experimental data and KS[18]analysis.
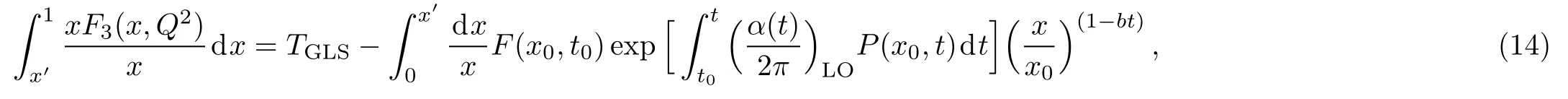
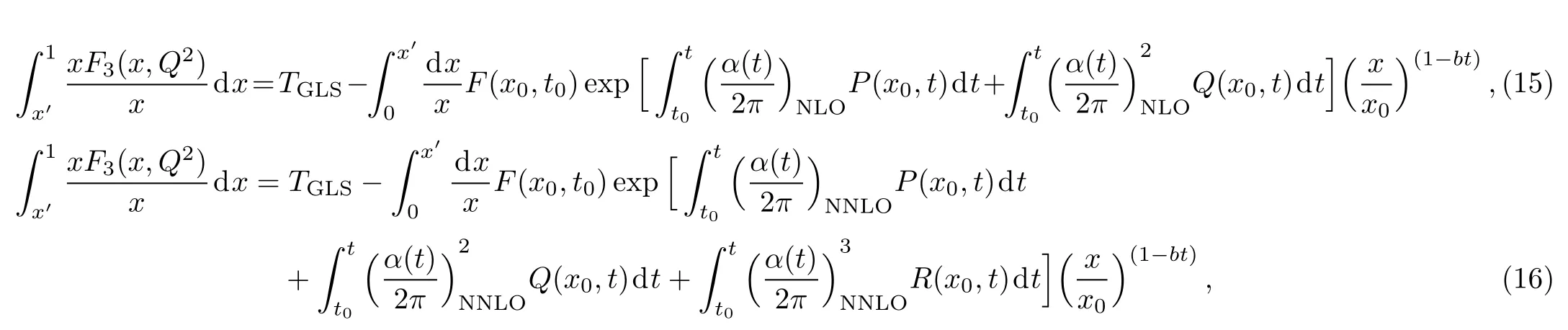
Detailed phenomenologicalanalysisperformed in Ref.[8]revealed that higher order pQCD corrections have a significant contribution towards the precise predictions of the structure functions as well as the sum rules.However recent analysis indicates that precise prediction of structure functions demand to incorporate several nonperturbative effects,in addition to pQCD corrections.There are several non-perturbative effects such as nuclear effects,higher twist effects,target mass corrections(TMC)etc.,to be incorporated into the joint QCD analysis of DIS structure functions and sum rules.However in accord with Ref.[19]the contribution due to TMC within the region of our consideration is neglected.In this paper we present an analysis of the NNLO results of xF3(x,Q2)structure function and the GLS sum rules taking into account the nuclear effects and Higher twist corrections.
2 Nuclear Shadowing E ff ect inxF3(x,Q2)Structure Function and GLS Sum Rule
2.1 Nuclear Shadowing E ff ect in xF3(x,Q2)Structure Function
The fact that the structure functions of bound and free nucleons are not equal was discovered in a deep inelastic muon experiment carried out by the European Muon Collaboration at CERN in 1982.[20]Since then the nuclear effect has been actively investigated with ever more sophisticated and ingenious deep inelastic scattering experiment with charged leptons and neutrinos.
Available experimental information on nuclear structure functions are mainly from charged-lepton DIS experiments performed at CERN,SLAC,DESY,FNAL and at JLab.In addition,data from the DrellYan reaction of protons o ffnuclear targets are also available.[21]The experiments usually measure the ratio R2(x,Q2)of the structure function F2(x,Q2)of a complex nucleus to deuterium.The studies on the behaviour of the ratio R2(x,Q2)as a function of x for a given fixed Q2re flects four distinct region of characteristic nuclear effects:shadowing region(x<0.1),anti-shadowing region(0.1
In addition to the charged-lepton DIS,neutrino DIS have also been a significant process for investigating the structures of hadrons and nuclei(see Refs.[22–28]and their references).Many ν-DIS experimental programmes,such as BEBC,[29]CDHS,[30]E545,[31]and,etc.,were carried out in order to have proper information about structure of nucleon,nuclear effect(EMC),mixing angle of weak interaction,etc. But none of them were able to confirm the EMC effect due to the presence of statistical uncertainties with the measurements. However it is expected that the measurements of differential cross-sections and structure functions in CCFR,[10?11]NuTeV,[12]CDHSW,[14]CHORUS,[13]and more recently in MINERvA,[32?33]through ν-DIS experiments would provide us better understanding about nuclear effect as well as internal structure of nucleon(see Ref.[34]for more details).
Along with the experimental efforts,several groups have been performed theoretical as well as phenomenological analysis of the nuclear effects in neutrino-nucleus DIS.Among them most prominent are the Kulagin and Petti(KP),[22?24]Qiu and Vitev(QV),[25]and Hirai,Komano and Naga(HKN)groups,[26,35]which have predicted the nuclear corrections in the low x region.Kulagin and Petti’s approach is quite different from the above ones in the sense that they try to calculate the nuclear corrections in conventional nuclear models as far as they can,and then they try to attribute remaining factors to o ff-shell effects of bound nucleons for explaining the data.
For simplicity,let us denote xF3(x,t)as F(x,t)and with this notation our results,Eq.(3),which predicts the xF3(x,Q2)structure functions for a nucleon(single or free)in NNLO pQCD corrections can be written as
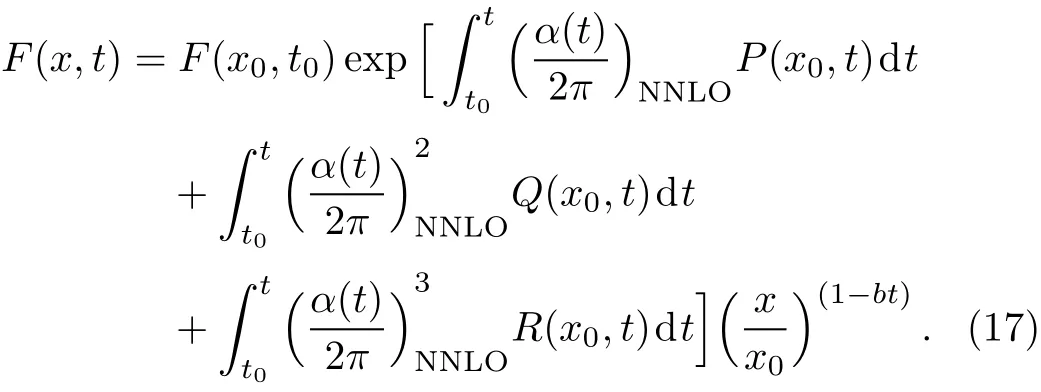
However in predicting the free nucleon structure functions,we need to consider the input point F(x0,t0),a free nucleon structure function at x=x0and t=t0.In our previous analysis performed in Ref.[8],the points were taken from the available experimental data.It is known that the experimental data for nucleon structure functions are extracted from nuclear targets and hence they are with several nuclear effects.Thus the experimental input points,we considered in our previous analysis are nothing but nuclear structure function FA(x0,t0),which in turn leads to inaccuracy in predicting free nucleon structure function.Therefore accurate prediction of free nucleon structure function requires a nuclear effect free input point.
The experimental results are the structure functions for bound nucleon FA(x,t)which is related to the free nucleon structure function as

Here FA(x,t)represents the nuclear structure function per nucleon and FN(x,t),the free nucleon structure function.At x=x0and t=t0,if we consider the value of the nuclear correction factor to be R(x,t)=R0,the input point in Eq.(17)can be replaced with FN(x0,t0)=FA(x0,t0)/R0and provides

Above expression is capable of predicting the free nucleon structure function through the experimental data FA(x0,t0)along with the correction factor R0.
Moreover,due to the unavailability of free nucleon structure function data,direct phenomenological analysis of Eq.(19)is not possible.In order to perform phenomenological analysis of our results with the experimental data either we need to remove nuclear effects from the data points or include the corresponding effects to our results of free nucleon.Here we have considered the later one,i.e.,we have incorporated the nuclear correction factor R(x)with our calculations as
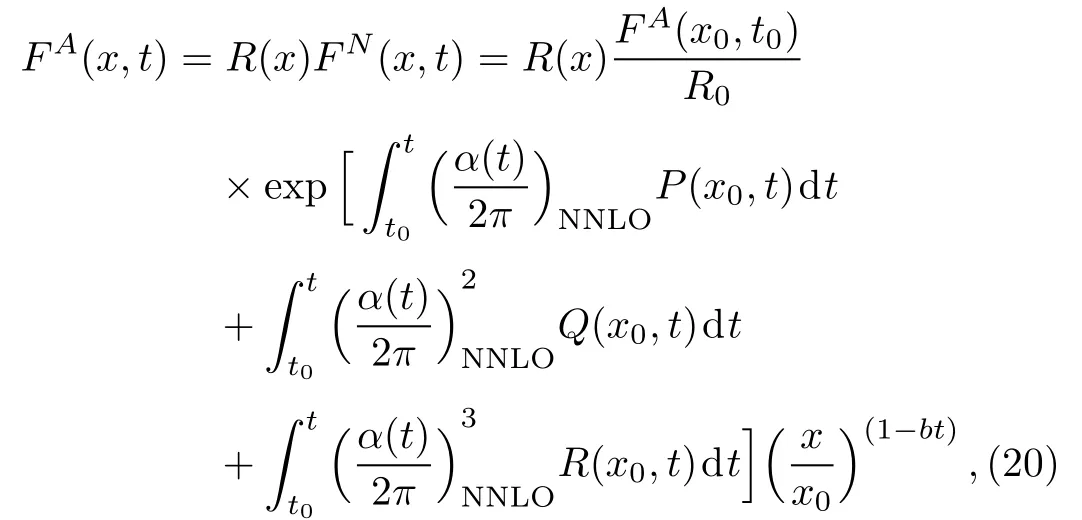
in order to describe properly the experimental results.
In this paper we have utilised the results for the nuclear correction factor R(x)predicted in KP.[22]Incorporating the corresponding corrections to our calculations of F(x,t)structure function,we have obtained the nuclear structure function F(A)(x,t)and depicted them in Fig.1.Here we have shown only the modification of our NNLO results in comparison with CCFR,NuTeV,CHORUS and CDHSW experimental data.We observe that our results for free nucleon structure functions,along with nuclear effect predicted by KP provide a well description of available experimental data for nuclear structure functions.
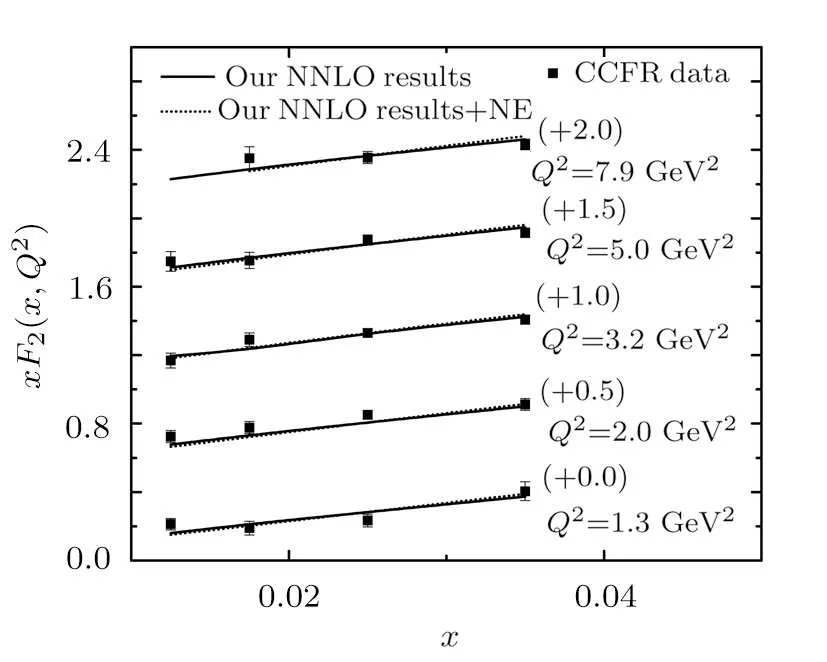
Fig.1 Our NNLO results for xF3(x,Q2)structure function with and without nuclear effect,in comparison with the CCFR[10]data.
2.2 Nuclear Shadowing E ff ect in GLS Sum Rule
Analogous to the structure functions,experimental determination of the DIS sum rules consists of considerable nuclear effects.As DIS sum rules are associated with the underlying symmetry as well as conservation laws of interactions,they provide strong normalization constraints on the structure functions.Therefore the sum rules are expected to provide an important bridge between different nuclear effects.In this section we brie fly discuss the nuclear effects in GLS sum rule based on several earlier analysis.We then incorporate possible nuclear corrections to our results Eq.(16)for GLS sum rule,obtained in the previous paper[8]and perform phenomenological analysis in comparison with the experimental measurements.
Experimental measurements of GLS sum rule was performed by CCFR and the results were extracted from Fe target.In order to compare our results for GLS sum rule obtained in Ref.[8],we refer the nuclear corrections estimated in Refs.[23–24].The detailed investigation on the nuclear corrections to GLS sum rule was performed in Ref.[23].They explicitly separated the nuclear corrections to the GLS integral as,whererefers to the GLS integral for nucleon.In accord with their predictions,the nuclear corrections to the GLS sum rule cancel out as x→0 in the leading order,which is due to the baryon charge conservation.They have also calculated the GLS integral,SGLSfor different nuclear targets.In Ref.[23],they obtained the corrections for iron and deuteron nuclei asandrespectively.In Ref.[23]they have nicely presented their result in Fig.10.From Fig.10 we observe that the nuclear correction δGLSdecreases progressively by increasing Q2.
The GLS sum rule for nuclei can be expressed as
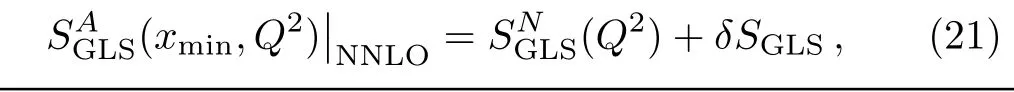
where the first term on the right hand side of above equation represents the GLS sum rule for free nucleon and the second term for the nuclear correction.Using the NNLO pQCD corrected expression(16)aswe get
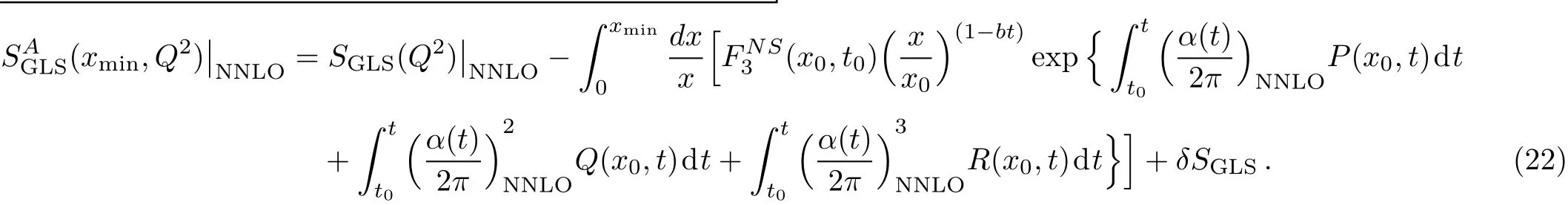
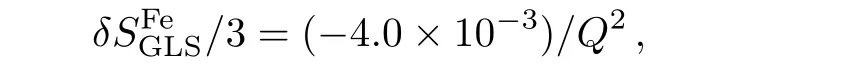
for the nuclear correction term,we have calculatedand depicted the results in Fig.2,in comparison with CCFR measurements of GLS sum rule with Fe as the target.In addition,we have plotted our NNLO results and the results of KS[18]prediction.From the figure we see that the our NNLO expression for GLSSR along with necessary nuclear correction has the capability of describing the experimental data of GLSSR for nuclei.
Now incorporating the KP[23?24]prediction

Fig.2 Our NNLO results for Gross–Llewelln Smith sum rule with and without nuclear effect,in comparison with those of CCFR measurements.(Q2’s are taken in the unit of GeV2).
3 Higher Twist Corrections on Structure Functions
The behaviour of the deep inelastic structure functions can be analyzed with the perturbative QCD.A method used for this analysis is the operator product expansion method(OPE).[36]The OPE is successful in describing the contributions from different quark-gluon operators to hadronic tensor and helps in ordering them according to their twist.In accord with OPE,the DIS structure functions and sum rules consist of two parts,the leading twist(LT)and the higher twist(HT)contributions:
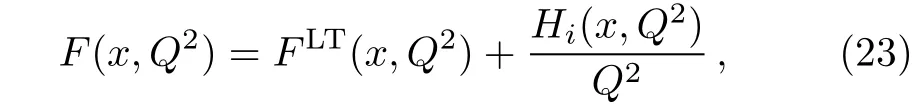
where i labels the type of the structure function(F=F2,F3,g1).The leading twist term is associated with the single particle properties of quarks and gluons inside the nucleon and is responsible for the scaling of DIS structure function via perturbative QCD αs(Q2)corrections.The higher twist terms re flect instead the strength of multiparton interactions(qq and qg).Since such interactions spoil factorization one has to consider their impact on the parton distribution functions extracted in the analysis of low-Q2data.Because of the non-perturbative origin it is difficult to quantify the magnitude and shape of the higher twist terms from first principles and current models can only provide a qualitative description for such contributions,which must then be determined phenomenologically from data.
The higher twist terms are governed by the terms contributing at different orders of 1/Q2:
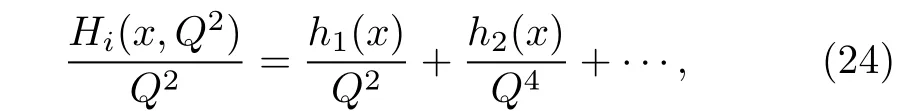
the leading term in this expansion is known as twisttwo,the sub-leading ones twist-three,etcetera. The higher twist terms are suppressed by terms of order 1/Q2,1/Q4,...,respectively.
The currently available experimental measurements of deep inelastic structure functions cover a wide range of x and Q2with ever increasing precision,which lead to an interesting challenge for theoretical physics in describing these data in the low-Q2domain.pQCD predictions,even with higher order corrections up to NNLO and NNNLO observed to be not sufficient for a precise description of deep inelastic structure function data,which in turn reveals that the discrepancy among data and pQCD predictions are not primarily the sub-leading terms in powers of αs,but corrections which are proportional to the reciprocal value of the photon virtuality Q2,viz.higher-twist terms.[37]
The extraction of higher twist terms from the data is a longstanding problem,as recognized from the very first developments of a pQCD phenomenology.[38?39]Existing information about higher twist terms in lepton-nucleon structure functions is scarce and somewhat controversial.Early analysis[40?41]suggested a significant HT contribution to the longitudinal structure function FL.The subsequent studies with both charged leptons[42?44]and neutrinos[17]raised the question of a possible dependence on order of QCD calculation used for the leading twist.The common wisdom is generally that HTs only a ff ect the region of Q2~ (1?3)GeV2and can be neglected in the extraction of the leading twist.
The higher twist terms are presently poorly known and currently are a subject of both theoretical and phenomenological studies(see Ref.[45]and the references therein).A better understanding of HT terms,in particular their role in describing low Q2and high x DIS data is important and provides valuable information on quark gluon correlations inside the nucleon.The importance of higher twist(HT)contribution to structure functions was pointed from the very beginning of QCD in comparison with experimental data[38]on structure functions.Several reports are available on the determination of the higher twist contributions in the electron-DIS structure functions(x,Q2)(see Refs.[46–48]for details)as well as neutrino-DIS structure function xF3(x,Q2).[49?53]Further,in general the higher twist corrections are also present in the case of polarized deeply inelastic scattering.But in this regard as the polarized structure functions are predicted in terms of an asymmetry,the effect of higher twist corrections in the denominator function needs to be known accurately.However,in Ref.[54]no signi ficant higher twist contributions were found.On the other hand some authors predicted(see for example Ref.[55])existence of higher twist contributions in the low x region,which is also the region of very low values of Q2.
The usual approach in analyses whose main aim is the extraction of leading twist PDFs is either to parametrize the higher twist contributions by a phenomenological form and fit the parameters to the experimental data,[56?57]or to extract the Q2dependence by fitting it in individual bins in x.[44,46?47,58?59]Such an approach effectively includes contributions from multiparton correlations(the true higher twist contributions)along with other power corrections that are not yet part of the theoretical treatment of DIS at low Q2.These include O(1/Q2)contributions such as jet mass corrections[60]and soft gluon resummation,[61]as well as contributions which are of higher order in αsbut whose logarithmic Q2behavior mimics terms∝1/Q2at low virtuality.[47,62]
In the following subsections we present a simple model in order to extract the higher twist contribution to xF3(x,Q2)structure function and GLS sum rule,along with comment on the phenomenological implications of our results.
3.1 Higher Twist in xF3(x,Q2)Structure Functions
In order to estimate the higher twist contribution to the xF3(x,Q2)structure function,we have performed an analysis based on a simple model.Here the first higher twist term is extracted and to do so we have parameterised the non-singlet structure functions as
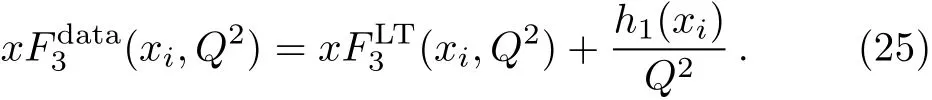
Here leading twist(LT)term corresponds to the pQCD contribution to structure functions and the constants h1(xi)(one per x-bin)parameterize the x dependence of higher twist contributions.For the leading twist term,we have utilised the results for the non-singlet structure functions obtained in our previous paper.[8]Incorporating our results for non-singlet structure functions in NNLO as the LT terms we have extracted the difference,from their corresponding experimental data and then fitted with h1(xi)/Q2.From the best fitting values,we have determined the higher twist contribution terms hiper x-bin.In this analysis we have performed our fitting analysis within the kinematical region 0.0125≤x≤0.5 and 1 GeV2≤Q2≤20 GeV2.
Incorporating the NNLO result(3)as the LT term,we have fitted the parametrization(25)with the CCFR,NuTeV,CHORUS and CDHSW data for the x-bins xi=0.0125,0.015,0.0175,0.025,0.035,0.045.Best fitted values of h1at different values of x are presented in Table 1 along with the χ2/d.o.f.value.
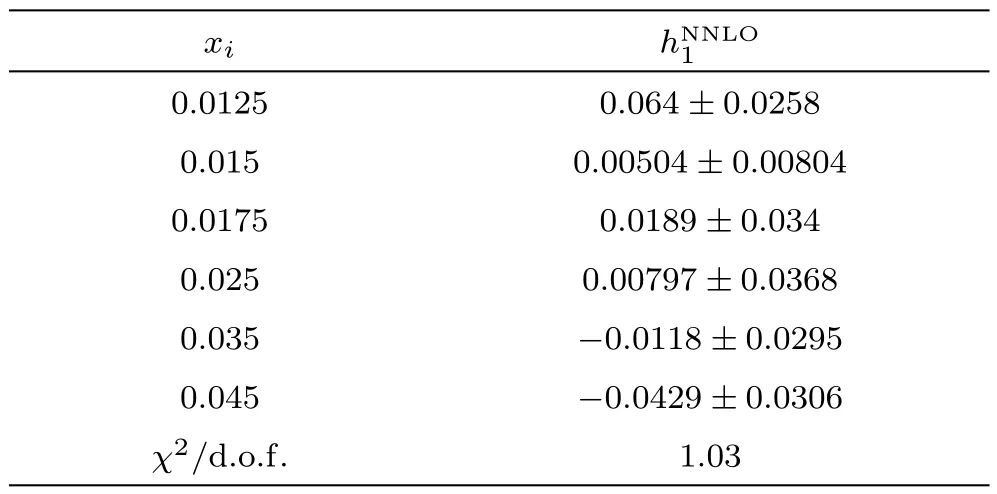
Table 1 Higher Twist corrections to xF3(x,Q2)structure function at NNLO.
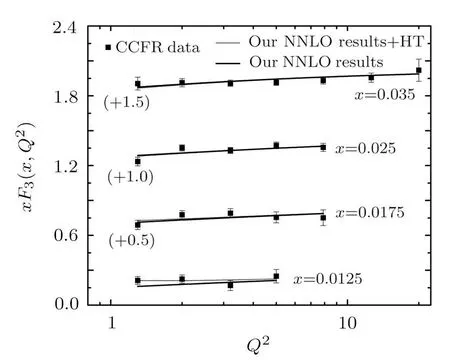
Fig.3 Higher twist corrections to xF3(x,Q2)structure function at NNLO.(Q2’s are taken in the unit of GeV2).
In Fig.3 we have presented the best fitting results of Eq.(25)for xF3(x,Q2)in comparison with CCFR experimental data.Here both the NNLO results,with HT and without HT are shown.Significant higher twist contribution to xF3(x,Q2)structure function is observed in the low-x,low-Q2region.We observe that our expressions along with the HT corrections provide better description of CCFR data than without HT within our kinematical region of consideration.
3.2 Higher Twist E ff ect in Gross-Llewellyn Smith Sum Rule
In the previous subsection,the higher twist effects in xF3(x,Q2)structure function is estimated by means of a simple model.We now extend the similar formalism in order to extract the higher twist contribution to the GLS sum rule associated with the xF3(x,Q2)structure function.Here we have parameterized the sum rule as
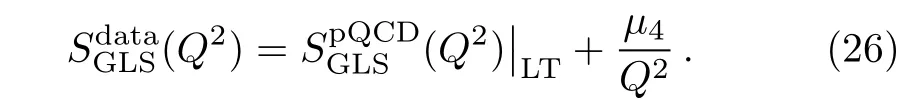
Here leading twist(LT)term corresponds to the pQCD contribution to the GLS sum rule andμ4signifies the contribution from first higher twist term.Incorporating the results in accord with our NNLO prediction,Eq.(16)in Eq.(26),we have fitted the expression with the available CCFR experimental data for GLSSR.The corresponding value ofμ4for which best fitting is obtained in NNLO are summarised in Table 2 along with the respective χ2/d.o.f values and in Fig.4 the results for GLS sum rule with and without HT are depicted.We observe that our expressions along with the HT corrections provide better description of experimental data for GLS sum rule.

Table 2 Higher Twist corrections to GLS sum rule at NNLO.
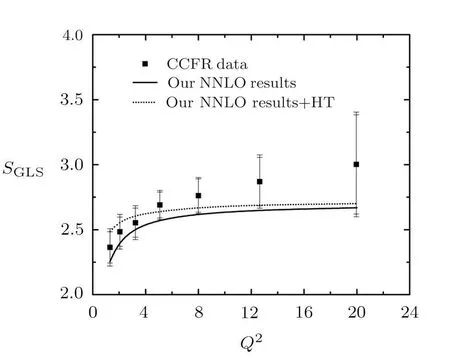
Fig.4 Higher twist corrections to GLS sum rule at NNLO.(Q2’s are taken in the unit of GeV2).
4 Conclusion
In this paper we present an analysis of the xF3(x,Q2)structure function and GLS sum rule taking into account the nuclear effect and higher twist effect.In this regard,special attention is given to the nuclear shadowing effect as we are mostly concerning with the small-x region.Incorporating the results of corrections due to shadowing nuclear effect obtained in earlier analysis for xF3(x,Q2)structure function as well as GLS sum rule to our results of the structure functions and sum rules for free nucleon,we obtain structure functions and sum rules for nuclei.Nuclear correction incorporated results are studied phenomenologically and it is observed that along with the nuclear correction,our NNLO results of the xF3(x,Q2)structure functions and GLS sum rule have the capability of providing well description of their respective experimental data collected using nuclear target.In addition,we have extracted the higher twist contributions to both the xF3(x,Q2)structure functions and GLS sum rule using a simple model and it is observed that our NNLO expressions for xF3(x,Q2)structure function and GLS sum rules along with the higher twist corrections provide well description of their respective experimental data.
[1]J.Blümlein,Prog.Part.Nucl.Phys.69(2013)28;A.De Roeck and R.S.Thorne,Prog.Part.Nucl.Phys.66(2011)727;A.M.Cooper-Sarkar,et al.,Int.J.Mod.Phys.A 13(1998)3385;M.Janbazi,N.Ghahramany,and E.Pourjafarabadi,Eur.Phys.J.C 74(2014)2718;N.Ghahramany,R.Khosravit,and S.Janipour,Phys.Part.Nucl.Lett.11(2014)186;C.Ayala and S.V.Mikhailov,Phys.Rev.D 92(2015)014028.
[2]V.N.Gribov and L.N.Lipatov,Sov.J.Nucl.Phys.15(1972)438;L.N.Lipatov,Sov.J.Nucl.Phys.20(1975)94;Y.L.Dokshitzer,Sov.Phys.JETP 46(1977)641;G.Altarelli and G.Parisi,Nucl.Phys.B 126(1977)297.
[3]R.Toldra,Comput.Phys.Commun.143(2002)287.
[4]N.Cabibbo and R.Petronzio,Nucl.Phys.B 137(1978)395.
[5]M.Gluck,E.Reya,and A.Vogt,Z.Phys.C 48(1990)471.
[6]G.R.Boroun,J.Exp.Theor.Phys.106(2008)700.
[7]P.K.Dhar and D.K.Choudhury,Indian J.Phys.87(2013)1041.
[8]N.M.Nath,M.K.Das,and J.K.Sarma,Indian J.Phys.90(2016)117.
[9]S.Moch,et al.,Nucl.Phys.B 688(2004)101;R.T.Herrrod and S.Wada,Phys.Lett.B 96(1980)195.
[10]W.G.Seligman,et al.,Phys.Rev.Lett.79(1997)1213
[11]W.C.Leung,et al.,Phys.Lett.B 317(1993)655.
[12]M.Tzanov,et al.,Phys.Rev.D 74(2006)012008.
[13]G.Onengut,et al.,Phys.Lett.B 632(2006)65.
[14]J.P.Berge,et al.,Z.Phys.C 49(1991)187.
[15]A.D.Martin,R.G.Roberts,W.J.Stirling,and R.S.Thorne,Eur.Phys.J.C 4(1998)463.
[16]H.L.Lai,et al.,Phys.Rev.D 55(1997)1280.
[17]A.L.Kataev,G.Parente,and A.V.Sidorov,Nucl.Phys.B 573(2000)405.
[18]A.L.Kataev and A.V.Sidorov,Phys.Lett.B 331(1994)179.
[19]J.Blümlein,et al.,Nucl.Phys.B 774(2007)182.
[20]J.J.Aubert,et al.,Phys.Lett.B 123(1983)275.
[21]D.M.Alde,,et al.,Phys.Rev.Lett.64(1990)2479;M.A.Vasilev,et al.,Phys.Rev.Lett.83(1999)2304;G.Moreno,et al.,Phys.Rev.D 43(9)(1991)2815.
[22]S.A.Kulagin and R.Petti,Nucl.Phys.A 765(2006)126.
[23]S.A.Kulagin and R.Petti,Phys.Rev.D 76(2007)094023.
[24]S.A.Kulagin and R.Petti,Nucl.Phys.A 640(1998)435.
[25]J.W.Qiu and I.Vitev,Phys.Lett.B 587(2004)52.
[26]M.Hirai,et al.,Phys.Rev.C 70(2004)044905.
[27]J.Nieves,EPJ Web of Conf.116(2016)11011.
[28]S.Gollapinni,arXiv:1602.05299v1[hep-ex](2016).
[29]A.M.Cooper,et al.,Phys.Lett.B 141(1984)133.
[30]H.Abramowicz,et al.,Z.Phys.C 25(1984)29.
[31]J.Hanlon,et al.,Phys.Rev.D 32(1985)2441.
[32]P.A.Rodrigues,et al.,Phys.Rev.Lett.116(2016)071802.
[33]J.Mousseau,et al.,Phys.Rev.D 93(2016)071101(R).
[34]C.G.Duan,G.L.Li,and P.N.Shen,Eur.Phys.C 48(2006)125.
[35]M.Hirai,et al.,Phys.Rev.C 76(2007)065207.
[36]K.G.Wilson,Phys.Rev.179(1969)1499;E.V.Shuryak and A.I.Vainshtein,Nucl.Phys.B 199(1982)451.
[37]J.Bartels and C.Bontus,arXiv:hep-ph/9908411[hep-ph](1999).
[38]L.F.Abbott and R.M.Barnett,Ann.Phys.125(1980)276;L.F.Abbott,et al.,Phys.Rev.D 22(1980)582;R.M.Barnett,Phys.Rev.Lett.48(1982)1657.
[39]A.De.Rujula,et al.,Ann.Phys.103(1977)315.
[40]J.L.Miramontes,et al,.Phys.Rev.D 40(1989)2184.
[41]L.W.Whitlow,et al.,Phys.Lett.B 250(1990)193.
[42]M.Virchaux and A.A.Milsztajn,Phys.Lett.B 274(1992)221.
[43]U.K.Yang and A.Bodek,Eur.Phys.J.C 13(2000)241.
[44]S.I.Alekhin,Phys.Rev.D 68(2003)014002.
[45]M.J.Glatzmaier,S.Mantry,and M.J.Ramsey-Musolf,Phys.Rev.C 88(2013)025202.
[46]M.Virchaux and A.A.Milsztajn,Phys.Lett.B 274(1992)221.
[47]J.Blümlein and H.B?ttcher,Phys.Lett.B 662(2008)336.
[48]J.Blümlein and H.B?ttcher,arXiv:0807.0248[hep-ph].
[49]I.S.Barker,et al.,Z.Phys.C 19(1983)147;I.S.Barker and B.R.Martin,Z.Phys.C 24(1984)255.
[50]J.Chyla and A.L.Kataev,Phys.Lett.B 297(1992)385.
[51]A.L.Kataev,et al.,Phys.Lett.B 417(1998)374.
[52]S.I.Alekhin and A.L.Kataev,Phys.Lett.B 452(1999)402.
[53]A.L.Kataev,et al.,Nucl.Phys.Proc.Suppl.79(1999)93.
[54]J.Blümlein and H.B?ttcher,Nucl.Phys.B 636(2002)225.
[55]E.Leader,et al.,Phys.Rev.D 73(2006)034023.
[56]S.Alekhin,et al.,AIP Conf.Proc.967(2007)215.
[57]J.Pumplin,et al.,J.High Energy Phys.2002(2002)012
[58]A.D.Martin,et al.,Eur.Phys.J.C 35(2004)325.
[59]A.D.Martin,et al.,Phys.Lett.B 443(1998)301.
[60]A.Accardi and J.W.Qiu,J.High Energy Phys.2008(2008)090.
[61]S.Schaefer,et al.,Phys.Lett.B 514(2001)284.
[62]S.Alekhin,Phys.Lett.B 488(2000)187.
 Communications in Theoretical Physics2016年12期
Communications in Theoretical Physics2016年12期
- Communications in Theoretical Physics的其它文章
- Quantum Private Comparison of Equality Based on Five-Particle Cluster State?
- Weibel Instability Growth Rate in Magnetized Plasmas with Quasi-Relativistic Distribution Function
- Physiological Flow of Jeffrey Six Constant Fluid Model due to Ciliary Motion
- Pressure Oscillating Flow in Corrugated Parallel Channel?
- Free Convective Nonaligned Non-Newtonian Flow with Non-linear Thermal Radiation
- Dilepton from Passage of Jets Through Spherical Expanding QGP?
