JIA Yan (賈 艷), LI Jin-hang (李晉航)

1 School of Construction and Management Engineering, Xihua University, Chengdu 610039, China

Scheduling Rules Based on Gene Expression Programming for Resource-Constrained Project Scheduling Problem

JIA Yan (賈 艷)1*, LI Jin-hang (李晉航)2

1SchoolofConstructionandManagementEngineering,XihuaUniversity,Chengdu610039,China

2DongfangElectricCorporationR&DCenter,IntelligentEquipmentandControlTechnologyInstitute,Chengdu611731,China

In order to minimize the project duration of resource-constrained project scheduling problem (RCPSP), a gene expression programming-based scheduling rule (GEP-SR) method is proposed to automatically discover and select the effective scheduling rules (SRs) which are constructed using the project status and attributes of the activities. SRs are represented by the chromosomes of GEP, and an improved parallel schedule generation scheme (IPSGS) is used to transform the SRs into explicit schedules. The framework of GEP-SR for RCPSP is designed, and the effectiveness of the GEP-SR approach is demonstrated by comparing with other methods on the same instances.

resource-constrainedprojectschedulingproblem(RCPSP);geneexpressionprogramming(GEP);schedulingrules(SRs)

Introduction

Resource-constrained project scheduling problem (RCPSP) is a well-known non-deterministic polynomial (NP)-hard problem and is widely studied by many researchers. In classical RCPSP, the currently schedulable activities compete for the limited resources, and the optimal scheduling sequence of these activities should be decided to minimize the project duration. There are many methods that have been used to deal with the problem and these methods can be categorized into three classes: (1) exact algorithms, such as integer programming[1]and branch-and-cut[2], which can provide optimal solutions, but the cost of computation time is huge even for a moderate size problem; (2) heuristic rules, such as shortest activity duration (SAD) and greatest resource demand (GRD)[3]; (3) search-based heuristic algorithms, such as genetic algorithm (GA)[4-5], particle swarm optimization (PSO)[6-7], ant colony optimization (ACO)[8-9], evolutionary programming (EP)[10], and differential evolution (DE)[11]. The solution qualities of heuristic rules are no better than the search-based methods. However, heuristic rules are used more widely in a real-world project due to the ease of implementation and low time complexity.

There are many human-made scheduling rules (SRs) used in the project scheduling, such as SAD, GRD, most successor operations (MSP), minimum latest finish time (MINLFT) and minimum slack (MINSLK) to determine which activity is to be scheduled earlier than others.In addition, Badiru[12]adopted the composite allocation factor (CAF) for each activity to determine resource allocation. CAF was computed as a weighted and scaled sum of resource allocation factor (RAF) and stochastic activity duration factor (SAF). An activity with a larger CAF value had the higher priority for resource allocation. Golenko-Ginzburg and Gonik[13]proposed a heuristic rule to solve RCPSP. The rule calculated the priority value for each unscheduled activity according to the average duration of the activity and its probability of being on the critical path during the project scheduling. The activity with bigger priority value was assigned the resources over the ones with lower priorities. They also built a zero-one integer programming model for the problem. Through comparison, the authors point out that for an NP-complete problem the zero-one integer programming becomes more difficult and heuristic solution is more suitable for practical applications. He and Zhang[14]proposed a dynamic priority rule-based forward-backward heuristic algorithm (FBHA) to minimize the fluctuation of resource usage in construction project. During the forward and backward iterations, FBHA adopted three kinds of priority rule sets,i.e., non-critical activities with their forward free float (FFF), forward total float (FTF) and backward free float (BFF) to determine the priorities of activities. Although, there are considerable heuristic rules, but as mentioned above, the search-based algorithms usually offer higher-quality solutions than heuristic rules. Therefore, there is a need to automatically construct and select more effective SRs.

In this research,in order to obtain the minimum project duration, a gene expression programming-based scheduling rule (GEP-SR) method is proposed to automatically discover and select the effective SRs which are based on the composition of project status and attributes of activities. Gene expression programming (GEP) is proposed by Ferreira[15], and is the natural development of GA and gene programming (GP). GEP is based on the Darwinian principle of reproduction and survival of the fittest and evolved through one or more genetic operators. GEP and GP with the same kind of diagram representation can be used to solve the complex problems that GA cannot. GEP and GP have been applied in job-shop scheduling problems[16-19], where they work as heuristic search algorithms to search the effective SRs but not those of potential scheduling solutions. Experimental results in Refs. [16-19] show that the SRs generated by GEP and GP outperform the human-made SRs. But for the same problems GP methods have more cost on computation time and the constructed rules are usually in a more complex formula than GEP. To our knowledge, however, GEP has seldom been used for the project scheduling problems, only Jedrzejowicz and Ratajczak-Ropel[20]proposed combining a multi-agent system with the GEP to obtain the schedule solutions for the RCPSP with time lags. Therefore, in this paper, the GEP-SR method is proposed to solve RCPSP in view of the minimal project duration. The best SR is constructed and selected by GEP from a number of candidates.

The remainder of the paper is organized as follows. Section 1 gives the statement of the RCPSP. Section 2 proposes the design of GEP-SR and its framework for RCPSP. The experiments and results are provided in section 3. Section 4 is the conclusions and future work.

1 Problem Statement

The RCPSP can be stated as follows: a project consists of activities from 1 toNwhere activities 1 andNare dummy activities, representing the start and the end of the project, respectively. These activities are subject to two kinds of constraints. The first is precedence constraint,i.e., one activityicannot start before all its predecessors have been finished. The second is resource constraint,i.e., activityirequires resources to be activated. There areKrenewable resource types, and the available amount of each resourcejisRj,j= 1, 2, …,K. Each activityihas a duration timedi, a start timesiand an end timeei, and requiresri junits of resourcejto be processed.

In this paper, the aim of RCPSP is to search the best SR corresponding to the minimal project duration under the precedence constraints and resource constraints.

2 Design of GEP-SR for RCPSP

In GEP, each chromosome is composed of elements from function set (FS) and terminal set (TS) related with a particular problem. GEP uses the elements in the predefined sets to discover possible solutions for the problem. When applying GEP to solving a specific project scheduling problem, the proper elements for FS and TS should be carefully selected and designed to satisfy the requirements of the algorithm.

2.1 TS

The elements in TS used to construct SRs are defined as the current status and attributes of the activities in the project. The attributes of activities affect the quality of scheduling results, and potentially, all of them can be considered to construct an SR, such as SAD, GRD, and MINLFT. In this paper, a small number of attributes of activities are used as follows.

(1) Current time (CT): the time when an activity is finished and the project starts to select another activity to process.

(2) Processing time (PT): the duration of an activityi,i.e., the value ofdi.

(3) Number of successor operations (NOP): the number of successor operations of an activity, which can be known from the precedence constraints in the project network.

(4) Resource number (RN): the total amount of resources required by activityi. The formulation is as follows:

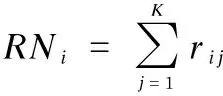
(1)

whereri jis the number of resource typejrequired by activityi, andKis the number of resource types involved.

(5) Sum of resource number (SRN): the sum of the maximum number of each resource type required by any activity in the project. The formulation is as follows:

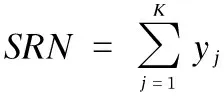
(2)

whereyjis the maximum number of resource typejrequired by any activity in the project, andKis the number of resource types involved.

These five parameters compose TS,i.e., TS = {CT, PT, NOP, RN, SRN}, where {CT, PT, NOP} is related with the precedence constraints and {RN, SRN} is concerned with the resource constraints. For each activity, every parameter in TS will have a specific numerical value during the project scheduling. Except the parameter CT, all of the other values can be known in advance from the precedence and resource constraints in the project network.

2.2 FS

For the construction of FS, similar to the other applications of GEP and GP in solving scheduling problems[16-19], four basic operators are used in this paper to express the corresponding arithmetic functions for creating our SRs,i.e., addition (“+”), subtraction (“-”), multiplication (“*”), and division (“/”) which returns 1 when the denominator is equal to 0. Therefore, TS and FS of GEP for RCPSP are expressed as follows:

= {CT, PT, NOP, RN, SRN},

= {+, -,

*, /},

where, the elements in TS denote the current status and attributes of the activities in the project, and the symbols in FS represent the mathematical operations between elements from TS.

2.3 Representation of GEP-SR for RCPSP

A gene in GEP is a fixed length string with a head and a tail. It is appointed that the head of gene may contain symbols from both the FS and the TS, whereas the tail consists only of symbols that come from the TS. For each problem, the length of the headhis chosen, then the length of the tailtis evaluated by the equationt=h*(n-1)+1, wherenis the maximum number of arguments for all operations in FS[15]. For a project scheduling problem, supposeh=6 andn=2, thent=7, which means that 6 symbols can be randomly selected from both {CT, PT, NOP, RN, SRN} and {+, -,

*, /} to compose the head of a gene, and 7 symbols randomly selected only from {CT, PT, NOP, RN, SRN} will form the tail of the gene. So the length of the gene is 6+7=13. One such gene is shown in Fig.1(a) (the tail is underlined).

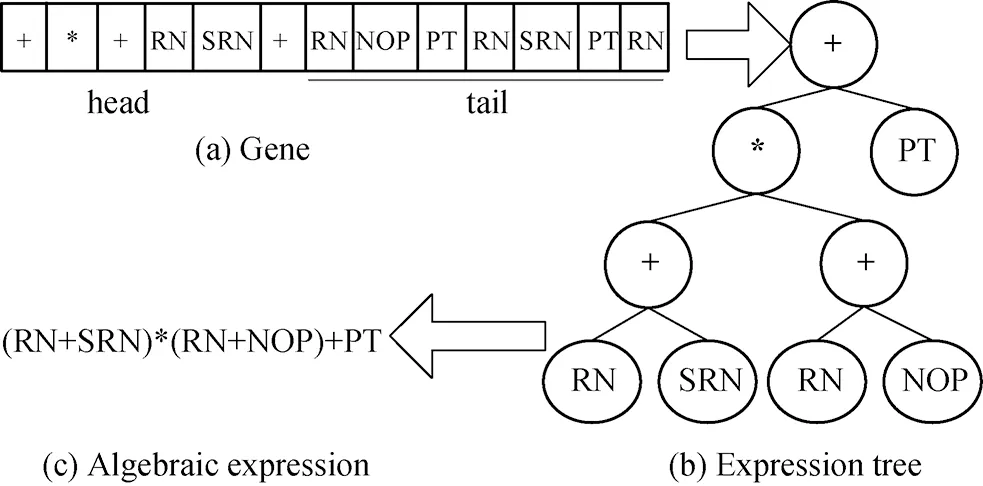
Fig.1 Gene construction and expression

A gene can be mapped into an expression tree (ET) following a depth-first, left to right way. The start position (position 0) in the gene corresponds to the root of the ET. Then, below each function symbol is attached as many branches as there are arguments to that function, and a branch of the ET stops growing when the last node in this branch is an element from the TS. In this case, the ET of the gene in Fig.1(a) is formed as Fig.1(b). The ET can be further interpreted in an algebraic expression (Fig.1(c)) which can be used as an SR to determine the priority values of activities during the project scheduling.

A chromosome of GEP can comprise one or more genes, and each gene codes for a sub-ET. Among the sub-ETs, the addition (“+”) and multiplication (“*”) functions are most used to link the sub-ETs into a final, multi-subunit ET[15]. In this paper, in order to reduce the complexity of the algebraic expression of final ET, the linking of two sub-ETs is used by addition (“+”) function.

2.4 Fitness function

Fitness function is used to evaluate the performance of chromosomes in the population, and it is the searching basis of evolution algorithms. The aim of RCPSP in our algorithm is to minimize the project duration, and the fitness function is defined as below:

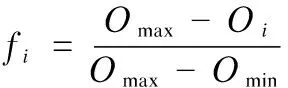
(3)

wherefiis the fitness of chromosomei;Oiis the project duration corresponding to chromosomei;OminandOmaxare the minimal and the maximal project durations corresponding to the chromosomes in the population, respectively.

2.5 Schedule generation from an SR

For heuristic algorithms, no matter what the environment of the project scheduling or the representation of the solution for the problem is, a solution should be transformed into an explicit schedule for evaluation. There are mainly two schedule generation schemes to build a schedule from a solution, the parallel schedule generation scheme (PSGS) and serial schedule generation scheme (SSGS). There are also two schedule generation directions, forward and backward.

In this paper, an SR represents a candidate solution to the problem, and an improved PSGS (IPSGS) with forward is adopted to generate a schedule for the RCPSP. The difference between IPSGS and classic PSGS lies in the following aspects. In the classic PSGS, the precedence constraints and resource constraints of the unscheduled activities are checked at the same time. However, in the IPSGS, the precedence constraints of the unscheduled activities will be checked at first, and then only the resource constraints of activities that are satisfied with the precedence constraints need to be checked. Thus, comparing with the classic PSGS, the IPSGS can reduce the number of scanning to some extent.

The heuristic procedure of IPSGS to generate an explicit schedule from an SR is shown in Fig.2 and described as follows.

Step 1 The CT is initialized as 0, and the list of activity end events (m_EEL) is initialized as empty, while the list of scanned activities (m_SL) is initialized as the activities that need to be scheduled in the project network.

Step 2 Check if there is any end event in m_EEL happening at CT. If No, then go to next step; if Yes, then release resources occupied by the activity that the current end event points to, and update the information of the resources,i.e., update the status and available amount of the resources. Then update the m_EEL,i.e., delete the current end event from m_EEL.

Step 3 Scan m_SL and check if there is any activity unscheduled. If No, then finish the procedure; if Yes, then construct the candidate activities list in which the activities are satisfied with the precedence constraints.

Step 4 Evaluate the priority values of these candidate activities with the given SR.

Step 5 Scan these activities one after another according to their priorities, and check if the resource constraints of the activity are satisfied. If Yes, then schedule this activity, including: update the available amount of resources occupied by this activity, compute the activity end event time (CT+di), and add it to m_EEL; if No, then go to next step.

Step 6 When all of the candidate activities have been scanned, CT is advanced to the earliest activity end event time in m_EEL.

This iterative process from Step 2 to Step 6 will be continued until the termination of the procedure. Finally, a feasible schedule will be generated, which is satisfied with the precedence and resource constraints of the project.

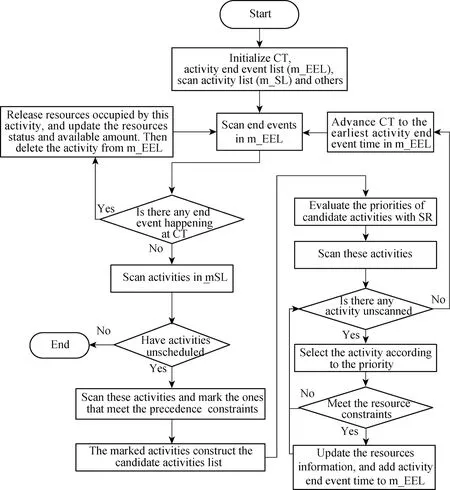
Fig.2 Procedure of IPSGS

2.6 Framework of GEP-SR for RCPSP

In this paper, the framework of GEP-SR integrates a simulation module with GEP module. The simulation module is used to describe the problem and generate the explicit schedules. While GEP works as a heuristic algorithm to search for SRs based on the scheduling results from the simulation. The framework of GEP-SR for RCPSP is shown in Fig.3 and explained as follows.

Step 1 The simulation model of the project scheduling problem is built to describe the problem.

Step 2 GEP randomly generates an initial population which consists of a number of chromosomes representing the candidate SRs.

Step 3 Together with the values of {PT, NOP, RN, SRN}of each activity, these SRs are passed to the simulation module and transformed into feasible schedules using IPSGS procedure. Then, the scheduling results of all candidate rules are passed back to the GEP module.

Step 4 The GEP module evaluates the fitness of all candidate rules according to their project durations. If the termination condition is not satisfied, then the next population is reproduced using GEP operators.

Step 5 The Step 3 and Step 4 are repeated until the termination condition is satisfied. Finally, the SR with the minimal project duration is selected for RCPSP as the best SR.

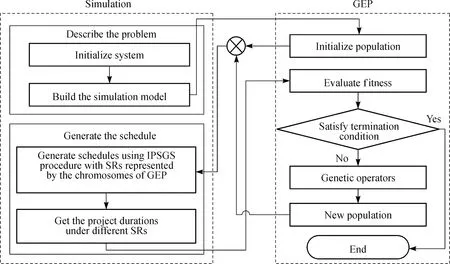
Fig.3 Framework of GEP-SR for RCPSP

3 Case Studies and Discussion

3.1 The selected test case

In order to verify the GEP-SR method for solving RCPSP, two data sets are selected for study. The first one is the well-known project scheduling problem LIBrary (PSPLIB) data set[21], which is used to compare our method with other SRs produced by human experience. The second one is the Patterson instance set with 110 test problems[22], which is applied to comparing our method with other procedures from the literature.

3.2 Parameter settings

In this paper, after extensive experiments,the parameter settings for GEP are shown in Table 1. Considering the random generation of some parameters in GEP, five runs are repeated for the parameter settings when solving the problem.

Table 1 Parameter settings for GEP

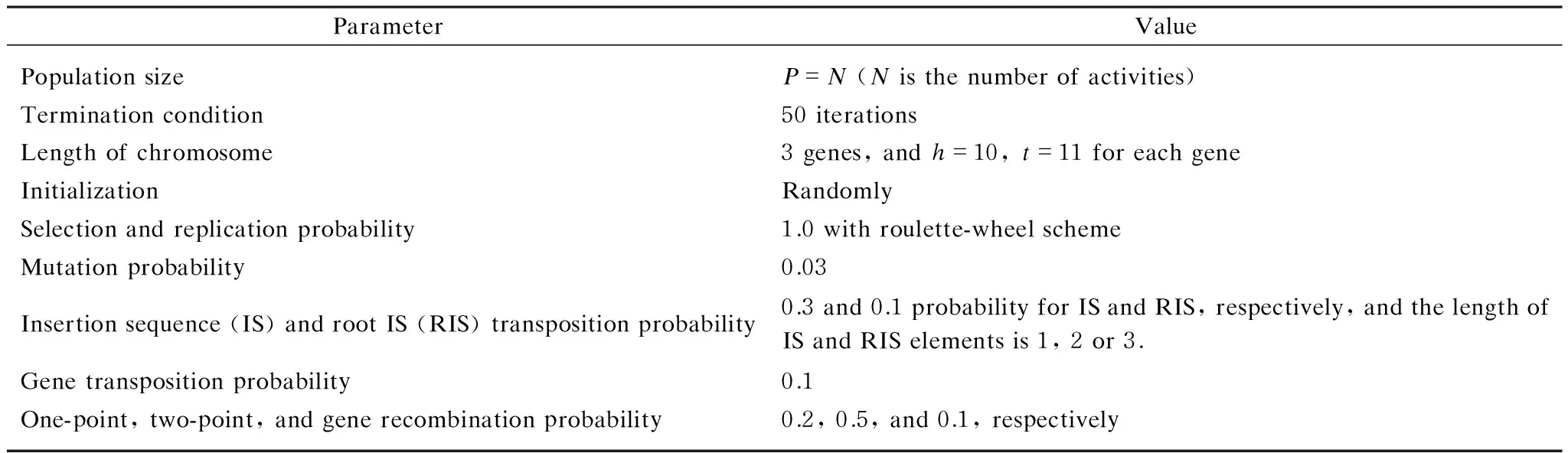
ParameterValuePopulationsizeP=N(Nisthenumberofactivities)Terminationcondition50iterationsLengthofchromosome3genes,andh=10,t=11foreachgeneInitializationRandomlySelectionandreplicationprobability1.0withroulette-wheelschemeMutationprobability0.03Insertionsequence(IS)androotIS(RIS)transpositionprobability0.3and0.1probabilityforISandRIS,respectively,andthelengthofISandRISelementsis1,2or3.Genetranspositionprobability0.1One-point,two-point,andgenerecombinationprobability0.2,0.5,and0.1,respectively

3.3 Experimental results

(1) Case study 1

The PSPLIB data set contains the sets J30, J60, J90, and J120 with 30, 60, 90, and 120 activities, respectively. The sets J30, J60, and J90 contain 48 different kinds of project structures while J120 consists of 60 different types of project structures, and 10 problem instances are randomly generated for each type. Using the 10 problems of the first type in each set, that is J301_1-J301_10, J601_1-J601_10, J901_1-J901_10, and J1201_1- J1201_10, we obtain a problem set with 40 instances. To be short, we call them the subsets J301, J601, J901, and J1201, respectively.

In order to demonstrate the effectiveness of the SRs found by GEP-SR method over other given traditional SRs, some rules produced by human experience such as MINSLK, MSP, SAD, RAF, MINLFT, and GRD are also selected to solve these test problems. The results of all evolved SRs and comparison with human-made rules are shown in Table 2.

Table 2 Results of evolved SRs and comparison with human-made rules

TestsetAverageprojectdurationunderthecorrespondingSRMINSLKMSPSADRAFMINLFTGRDRule1Rule2Rule3Rule4J30169.072.375.175.366.370.653.154.753.354.8J601114.0119.2122.6119.3108.9123.686.683.586.584.8J901144.9146.2157.8151.2134.8155.095.698.194.598.1J1201193.5196.4205.2200.4180.7203.5129.1130.7127.8126.5Total521.4534.1560.7546.2490.7552.7364.4367.0362.1364.2

For the chosen instances, the GEP-SR evolves four different SRs out of each individual test set, which are Rule1, Rule2, Rule3 and Rule4 for subsets J301, J601, J901, J1201, respectively. These rules are the ones that produce the best overall performance in the five independent runs, and the simplified formulations are as follows.

Rule1: 3CT+NOP2+RN+RN/SRN.

Rule2: CT+NOP2/(NOP+SRN+(PT+RN)/RN)+SRN*CT.

Rule3: (RN2+RN)/SRN+CT+NOP.

Rule4: SRN-NOP+CT*NOP+CT/PT+RN.

In Table 2, the italics (i.e., 53.1, 83.5, 94.5, and 126.5) indicate the average project durations of the test sets J301, J601, J901, and J1201 under Rule1, Rule2, Rule3, and Rule4, respectively. We can see that the SR out of specific type of project is more suitable to solve this type of problem.

From the individual and cumulative performances of each of these rules in Table 2, it also can be seen that no rule performs consistently better than all other rules for any kinds of project problems, but the overall performance of Rule3 produced by GEP-SR is better than any other of the SRs involved in the table. In addition, from the comparison of GEP-SR and SRs produced by human experience, it is shown that the performance of the SRs constructed by GEP is much better than those by human-made.

(2) Case study 2

Another data set to study the GEP-SR method for RCPSP is the Patterson instance set with 110 test projects. The 110 projects are different scheduling problems, and the GEP-SR framework is used to search the best SR with the minimum project duration for each of the problem. In addition, in order to demonstrate the effectiveness of GEP-SR, other heuristics applied by Depuy and Whitehouse[23]are used to compare with our method on the Patterson instances.

The Patterson instance set was adopted by Depuy and Whitehouse[23]to investigate their heuristic approach called computer method of sequencing operations for assembly lines (COMSOAL) which was first developed as a computer method to solve the assembly line balancing problem. To study the benefit of solving the scheduling network forward versus backward, each problem was solved forward, backward, and half-forward and half-backward (i.e., F, B, and F and B), respectively. And to verify their method, the COMSOAL results were compared to several well-known resource allocation heuristics, where the authors selected ACTIM, latest finish time (LFT), resources over time (ROT), ACTRES, and the combination of them. More details may refer to Ref.[23].

Using the settings of the parameters in Table 1, the GEP-SR is compared with COMSOAL with F, COMSOAL with B, and COMSOAL with F and B directions after 50 iterations, respectively. For the 110 test instances, the comparison results of GEP-SR and heuristics from Ref.[23] are shown in Table 3. In Table 3, BEST2, BEST3, and BEST4 are the best combinations of 2, 3, and 4 heuristics. BEST2 uses ACTIM and LFT; BEST3 uses ACTIM, LFT, and ROT; and BEST4 uses ACTIM, LFT, ROT, and ACTRES.

Table 3 Comparison results of GEP-SR and other heuristics

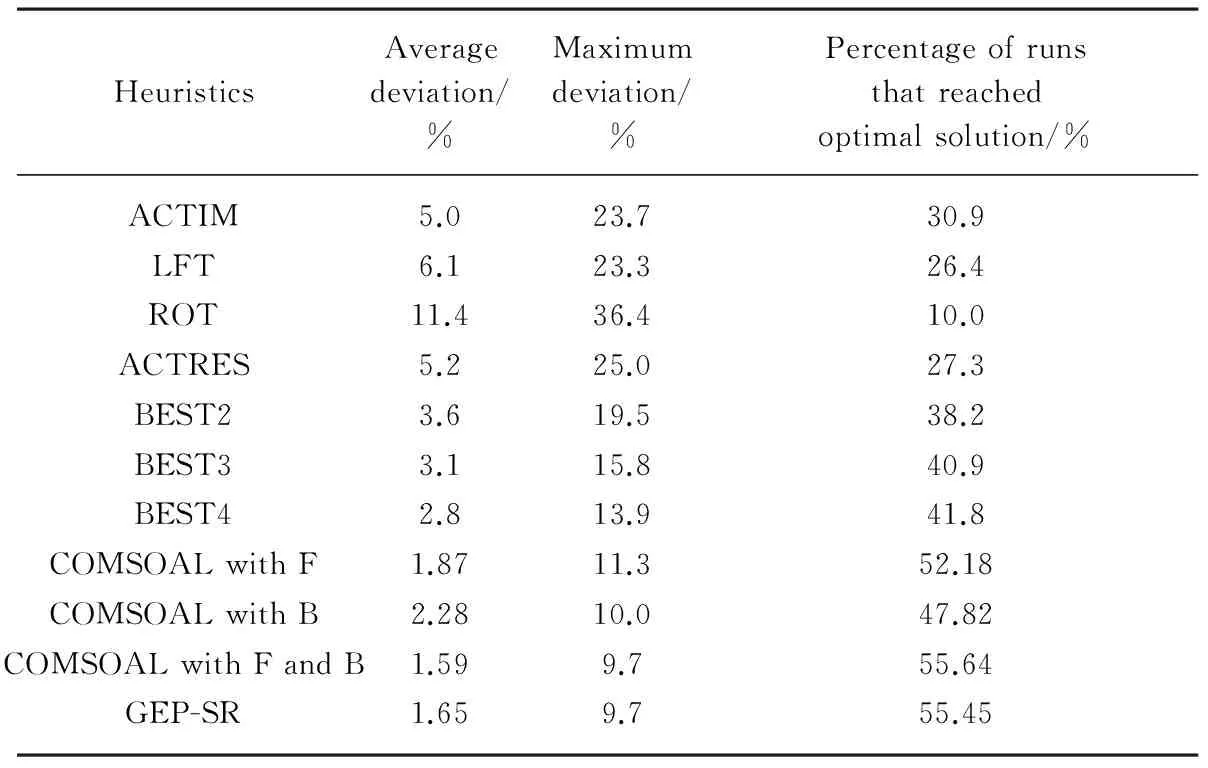
HeuristicsAveragedeviation/%Maximumdeviation/%Percentageofrunsthatreachedoptimalsolution/%ACTIM5.023.730.9LFT6.123.326.4ROT11.436.410.0ACTRES5.225.027.3BEST23.619.538.2BEST33.115.840.9BEST42.813.941.8COMSOALwithF1.8711.352.18COMSOALwithB2.2810.047.82COMSOALwithFandB1.599.755.64GEP-SR1.659.755.45

From Table 3, the performance of the combination rules is better than the single rules; the performance of the COMSOAL with any direction is better than any other human-made rules, and the performance of COMSOAL with F and B direction is better than COMSOAL with F or B; and the performance of GEP-SR is better than single rules, combination rules, COMSOAL with F, and COMSOAL with B, and is close to COMSOAL with F and B. Therefore, it is shown that GEP-SR is one of the effectiveness methods for solving the RCPSP.

4 Conclusions

In this paper, a GEP-SR approach is proposed to discover effective SRs for solving the RCPSP. These SRs are based on the combination of current status and attributes of activities. The application of GEP-SR framework for RCPSP is designed, where GEP works as a heuristic algorithm to automatize synthesis and search for SRs. Based on the experimental results, it can be concluded that GEP-SR is an efficient way to find good solutions to the project scheduling problems.

Future research will concentrate on finding other potential functions, such as logical functions or conditional functions, into function set to express the SRs more effectively, and testing more effective operators to improve GEP search ability.

[1] Talbot F B. Resource-Constrained Project Scheduling with Time-Resource Tradeoffs: the Nonpreemptive Case [J].ManagementScience, 1982, 28(10): 1197-1210.

[2] Kis T. A Branch-and-Cut Algorithm for Scheduling of Projects with Variable-Intensity Activities [J].MathematicalProgramming, 2005, 103: 515-539.

[3] Davis E W, Patterson J H. A Comparison of Heuristic and Optimum Solutions in Resource-Constrained Project Scheduling [J].ManagementScience, 1975, 21(8): 944-955.

[4] Debels D, Vanhoucke M. A Decomposition-Based Genetic Algorithm for the Resource-Constrained Project-Scheduling Problem [J].OperationsResearch, 2007, 55(3): 457-469.

[5] Zamani R. A Competitive Magnet-Based Genetic Algorithm for Solving the Resource-Constrained Project Scheduling Problem [J].EuropeanJournalofOperationalResearch, 2013, 229(2): 552-559.

[6] Zhang H, Li X D, Li H,etal. Particle Swarm Optimization-Based Schemes for Resource-Constrained Project Scheduling [J].AutomationinConstruction, 2005, 14(3): 393-404.

[7] Jia Q, Seo Y.An Improved Particle Swarm Optimization for the Resource-Constrained Project Scheduling Problem [J].TheInternationalJournalofAdvancedManufacturingTechnology, 2013, 67(9/10/11/12): 2627-2638.

[8] Merkle D, Middendorf M, Schmeck H. Ant Colony Optimization for Resource-Constrained Project Scheduling [J].IEEETransactionsonEvolutionaryComputation, 2002, 6(4): 333-346.

[9] Zhang H. Ant Colony Optimization for Multimode Resource-Constrained Project Scheduling [J].JournalofManagementinEngineering, 2012, 28(2): 150-159.

[10] Sebt M H, Alipouri Y. Solving Resource-Constrained Project Scheduling Problem with Evolutionary Programming [J].JournaloftheOperationalResearchSociety, 2013, 64(9): 1327-1335.

[11] Cheng M Y, Tran D H, Wu Y W. Using a Fuzzy Clustering Chaotic-Based Differential Evolution with Serial Method to Solve Resource-Constrained Project Scheduling Problems [J].AutomationinConstruction, 2014, 37: 88-97.

[12] Badiru A B. A Simulation Approach to PERT Network Analysis [J].Simulation, 1991, 57(4): 245-255.

[13] Golenko-Ginzburg D, Gonik A. Stochastic Network Project Scheduling with Non-consumable Limited Resources [J].InternationalJournalofProductionEconomics, 1997, 48(1): 29-37.

[14] He L H, Zhang L Y. Dynamic Priority Rule-Based Forward-Backward Heuristic Algorithm for Resource Levelling Problem in Construction Project [J].JournaloftheOperationalResearchSociety, 2013, 64(8): 1106-1117.

[15] Ferreira C. Gene Expression Programming: a New Adaptive Algorithm for Solving Problems [J].ComplexSystems, 2001, 13(2): 87-129.

[16] Dimopoulos C, Zalzala A M S. Investigating the Use of Genetic Programming for a Classic One-Machine Scheduling Problem [J].AdvancedinEngineeringSoftware, 2001, 32(6): 489-498.

[17] Tay J C, Ho N B. Evolving Dispatching Rules Using Genetic Programming for Solving Multi-objective Flexible Job-Shop Problems [J].Computers&IndustrialEngineering, 2008, 54(3): 453-473.

[18] Nie L, Shao X Y, Gao L,etal. Evolving Scheduling Rules with Gene Expression Programming for Dynamic Single-Machine Scheduling Problems [J].InternationalJournalofAdvancedManufacturingTechnology, 2010, 50(5/6/7/8): 729-747.

[19] Nie L, Gao L, Li P G,etal. A GEP-Based Reactive Scheduling Policies Constructing Approach for Dynamic Flexible Job Shop Scheduling Problem with Job Release Dates [J].JournalofIntelligentManufacturing, 2013, 24(4): 763-774.

[20] Jedrzejowicz P, Ratajczak-Ropel E. Agent-Based Gene Expression Programming for Solving the RCPSP/Max Problem [J].LectureNotesinComputerScience, 2009, 5495: 203-212.

[21] Kolisch R, Sprecher A. PSPLIB—a Project Scheduling Problem Library: OR Software-ORSEP Operations Research Software Exchange Program [J].EuropeanJournalofOperationalResearch, 1996, 96: 205-216.

[22] Patterson J H. A Comparison of Exact Approaches for Solving the Multiple Constrained Resource, Project Scheduling Problem [J].ManagementScience, 1984, 30(7): 854-867.

[23] Depuy G W, Whitehouse G E. Applying the COMSOAL Computer Heuristic to the Constrained Resource Allocation Problem [J].Computers&IndustrialEngineering, 2000, 38(3): 413-422.

Foundation item: The Spring Plan of Ministry of Education, China (No. Z2012017)

TP391 Document code: A

1672-5220(2015)01-0091-06

Received date: 2014-03-06

* Correspondence should be addressed to JIA Yan, E-mail: jiayan_1015@163.com