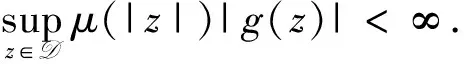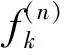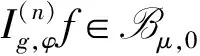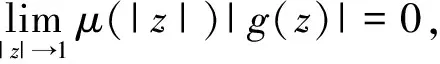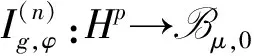Generalized integration operators from Hardy spaces
Qu Huiying
(School of Mathematics & Statistics,Jiangsu Normal University,Xuzhou 221116,Jiangsu,China)
0 Introduction
Let D denote the open unit disk of the complex plane C and H(D) the space of all analytic functions in D.
A positive continuous functionνon the interval [0,1) is called normal[1], if there areδ∈[0,1) anda,b, 0 is decreasing on [δ,1) If we say that a functionν: D→[0,1) is normal, we also assume that it is radial, i.e.ν(z)=ν(|z|),z∈D. For 0 For 0 Letμbe a weight, that is,μis a positive continuous function on D. The Bloch-type Bμconsists of allf∈H(D) such that With the norm ‖f‖Bμ=|f(0)|+bμ(f), it becomes a Banach space. The little Bloch-type space Bμ,0is a subspace of Bμconsisting of thosef∈Bμ, such that Here we quote some auxiliary results which will be used in the proofs of the main results in this paper. Lemma1[2]Forp>1, there exists a constantC(p) such that Lemma2[16]Suppose that 0 for everyz∈D and all nonnegativen=0,1,2,…. Lemma4A closed setKin Bμ,0is compact if and only ifKis bounded and satisfies The proof is similar to that of Lemma 1 in [17], so we omit it. (1) ProofAssume that (1) holds. Then for everyz∈D andf∈Hp, by Lemma 2, we have (2) For a fixedω∈D, set we get that From Lemma 1, we have Hence, (3) Forω∈D, by (3) we have ≤C<∞, (4) and from (3), we obtain that ≤C<∞. (5) Thus combining with (4), (5), we get the condition (1). (6) and (7) We assume that ‖fk‖p≤1. From (7), we have for anyε>0, there existsρ∈(0,1), whenρ<|φ(z)|<1, we have (8) ≤(M+C)ε. (9) We can use the test functions Note that (10) From (10) and |φ(zk)|→1, it follows that and consequently (7) holds. (11) (12) Then for anyf∈Hp, from Lemma 2, we obtain that then (12) holds. From (7), it follows that for everyε>0, there existsδ∈(0,1), such that (13) whenδ<|φ(z)|<1. Using (12), we see that there existsτ∈(0,1) such that (14) whenτ<|z|<1. Therefore whenτ<|z|<1 andδ<|φ(z)|<1, by (13), we have (15) On the other hand, whenτ<|z|<1 and |φ(z)|≤δ, by(14), we obtain (16) From (15) and (16), (11) holds. The proof is completed. AcknowledgmentsThe author thanks the referee(s) for carefully reading the manuscript and making several useful suggestions for improvement. The author is also indebted to Professor Liu Yongmin, who gave him kind encouragement and useful instructions all through his writing. : [1] Shields A L,Williams D L.Bounded projections,duality,and multipliers in space of analytic functions[J].Trans Amer Math Soc,1971,162:287. [2] Duren P L.Theory ofHPspaces[M].New York:Academic Press,1970. [3] Garnett J B.Bounded analytic functions[M].New York:Springer,2007. [4] Zhu K.Bloch type spaces of analytic functions[J].Rochy Mount J Math,1993,23(3):1143. [5] Sharma S D,Sharma A.Generalized integration operators from Bloch type space to weighted BMOA spaces[J].Demonstr Math,2011,44(2):373. [7] Yu Yanyan.Volterra-type composition operators from logarithmic Bloch spaces into Bloch-type spaces[J].J Xuzhou Norm Univ:Nat Sci Ed,2009,27(3):14. [9] Yang Weifeng.Composition operators fromF(p,q,s) spaces to thenth weighted-types paces on the unit disc[J].Appl Math Comput,2011,218(4):1443. [10] Zhu Xiangling.Generalized composition operators from generalized weighted Bergman spaces to Bloch type spaces[J].J Korean Math Soc,2009,46(6):1219. [11] Ohno S.Products of composition and differentiation between Hardy spaces[J].Bull Aus tral Math Soc,2006,73(2):235. [12] Zhu Xiangling.Products of differentiation,composition and multiplication from Bergman typespaces to Bers type spaces[J].Integr Transf Spec Funct,2007,18(3/4):223. [13] Liu Xiaoman,Yu Yanyan.The product of differentiation operator and multiplication operator fromH∞to Zygmund spaces[J].J Xuzhou Norm Univ:Nat Sci Ed,2011,29(1):37. [14] Zhu Xiangling.An integral-type opreator fromH∞to Zygmund-type spaces[J].Bull Malays Math Sci Soc,2012,35(3):679. [15] He Zhonghua,Gao Guangfu.Generalized integration operators between Bloch-type spaces andF(p,q,s) spaces[J].Taiwanese J Math,2013,17(4):2658. [16] Ye Shanli,Zhou Zhonghua.Weighted composition operators from Hardy to Zygmund type spaces[J].Abstr Appl Anal,2013,2013(10):286. [17] Madigan K,Matheson A.Compact composition operator on the Bloch space[J].Trans Amer Math Soc,1995,347(7):2679.
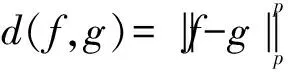
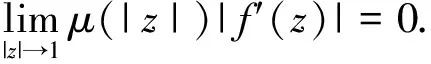

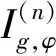
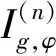
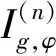

1 Preliminary material


2 Boundedness and compactness of from Hp (0