Tang Chuanye Chen Xiyuan Song Rui

(School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China)(Key Laboratory of Micro-Inertial Instrument and Advanced Navigation Technology of Ministry of Education,Southeast University, Nanjing 210096, China)

?

An approach to improving maneuver performanceof coning algorithm

Tang Chuanye Chen Xiyuan Song Rui

(School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China)(Key Laboratory of Micro-Inertial Instrument and Advanced Navigation Technology of Ministry of Education,Southeast University, Nanjing 210096, China)

Aiming to improve the maneuver performance of the strapdown inertial navigation attitude coning algorithm, a new coning correction structure is constructed by adding a sample to the traditional compressed coning correction structure. According to the given definition of classical coning motion, the residual coning correction error based on the new coning correction structure is derived. On the basis of the new structure, the frequency Taylor series method is used for designing a coning correction structure coefficient, and then a new coning algorithm is obtained. Two types of error models are defined for the coning algorithm performance evaluation under coning environments and maneuver environments, respectively. Simulation results indicate that the maneuver accuracy of the new 4-sample coning algorithm is almost double that of the traditional compressed 4-sample coning algorithm. The new coning algorithm has an improved maneuver performance while maintaining coning performance, compared to the traditional compressed coning algorithm.

coning algorithm; coning correction structure; maneuver performance; coning performance; frequency Taylor series method

In recent decades, it has always been an attractive task to design an efficient coning algorithm which includes designing an efficient coning correction structure and optimizing the structure coefficient. Miller[1]first presented a three-sample algorithm structure and an approach to designing the coning algorithm in a pure coning environment by truncating the frequency Taylor series of updating rotation vector error. Lee et al.[2]further applied Miller’s idea and arrived at the conclusion that the uncompressed coning correction structure exists in redundancy under coning conditions. According to this conclusion, Ignagni[3]verified that the cross product of both integral angular rate samples is independent of absolute time, and it is merely a function of the time interval between sampling points under coning conditions. Also, Ignagni[3]first designed the compressed coning correction structure and the compressed coning algorithm. Unlike the previous coning algorithms for gyro error-free output, Mark et al.[4]presented a method of tuning a high-order coning algorithm to match the frequency response characteristics of a gyro with filtered output. Based on the compressed coning correction structure, Savage[5]first raised the idea of using the least square method to design the coning correction algorithm for balanced coning performance over a coning frequency range. Subsequently, Savage[6]further applied the least square method to coning algorithm design in pseudo-coning environments. Tang et al.[7]introduced the least square method into the angular rate-based attitude algorithm design. Subsequently, Tang et al.[8-9]presented a new type of angular rate-based coning correction structure for coning error compensation. Chen et al.[10]proposed an improved coning algorithm based on the second optimization method. Song et al.[11]concentrated on the improvement of maneuver accuracy of coning algorithms, and developed an approach to recovering the maneuver accuracy of classical coning algorithms by combining the earliest time Taylor series method and the latest frequency methods. Tang et al.[12]later proposed a half-compressed coning correction structure to improve the maneuver accuracy of classical coning algorithms and to achieve a balance between algorithm accuracy and the throughput.

This paper first presents a new coning correction structure, which is constructed by adding a sample to the traditional compressed coning correction structure. The frequency Taylor series method is used for the coning algorithm design based on the new structure. Simulation results indicate that the new coning algorithm shows an improved maneuver performance compared to the traditional compressed algorithm, owing to the rationality of the new structure.

1 Coning Correction Structure

Generally, the rotation vectorφlfor the attitude update is calculated by using a simple form to approximate the integral of the rotation vector differential equation. A commonly used approximation form[3,5-12]can be written as

φl=αl+δφl

αl=α(tl,tl-1)

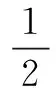
(1)

wheretis the time;αlis the integral of the gyro-sensed angular rateωfrom timetl-1to timetl; δφldenotes the coning correction.

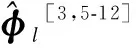
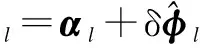
(2)

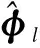
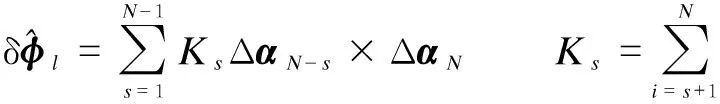
(3)

Both traditional coning correction forms defined by Eqs.(2) and (3) are equivalent under coning motion conditions, but not equivalent under maneuver conditions. Song et al.[11]indicated that the algorithm based on Eq.(2) can achieve much higher maneuver accuracies, but requires more throughput than those based on Eq.(3). This paper proposes a new coning algorithm differing from the traditional coning algorithm:

(4)

whereJsis the coning correction coefficient;θNis the sum of the last two angular increments selected from all samples over timetl-1totl, and it can be directly obtained from the process of computingαlin Eq.(2).

2 Coning Correction Algorithm

2.1 Correction coefficient design

Assume that the body is undergoing the pure coning motion defined by the angular rate vector[3,5,6,9,12],

(5)

whereω(t) is an angular rate vector in the body frame at timet;aandbare the amplitudes of the angular oscillations in two orthogonal axes of the body;Ωis the frequency associated with the angular oscillations.

Based on the coning motion angular rate vector definition by Eq.(5), Ignagni[3]derived the analytical value of the coning correction δφlin Eq.(1) withtl=tl-1+Tl=tl-1+LTk:

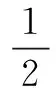
(6)

whereβis a coning frequency parameter relevant toTk.

Under the coning motion defined by Eq.(5), the angular increment Δαkis obtained by integrating the angular rate vectorω(t) fromtl-(N-k+1)Tktotl-(N-k)Tk.

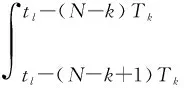
(7)

Also, the angular incrementθNis obtained by integrating the angular rate vectorω(t) fromtl-2Tktotl.

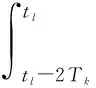
(8)

Then the cross product Δαk×θNis derived from Eqs.(7) and (8) as

Δαk×θN=

(9)

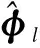
fs(β)≡ sin(sβ)+sin[(s-1)β]-

sin[(s+1)β]-sin[(s-2)β]

(10)

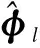
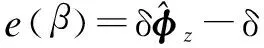
(11)

Substituting Eq.(6) and Eq.(10) into Eq.(11) gives

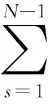
(12)

According to the Taylor series expansion of sinβaround zero point, we have

(13)

Then the errore(β) in Eq.(12) can be expanded as a Taylor series form around zero point,

(14)

Setting the coefficients of the firstN-1 terms of Taylor series Eq.(14) to zeros, we can obtain the system of linear equations, which can be simplified as

(15)

Defining terms

J=(Js,1)(N-1)×1Js,1≡Js

B=(bk,1)(N-1)×1bk,1≡-L2k+1

(16)

Then the systems of linear equations (16) can be rewritten in the following matrix form:

AJ=B

(17)

whereAis anN-1 byN-1 square matrix whosek-th row ands-th column component isaks;Bis anN-1 by one column matrix formed from componentsbk,1s;Jis anN-1 by one column matrix formed from componentsJs,1s. Solving Eq.(17), we obtain the optimized coning correction coefficientsJss, which are applicable to the coning correction form defined by Eq.(4).

J=A-1B

(18)

2.2 Algorithm performance evaluation

Two types of error models are defined to evaluate the coning algorithm performance under coning and maneuver environments.

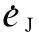
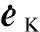
(20)

For evaluating the algorithm performance in maneuver environments, assume that the body is undergoing a maneuver angular motion characterized by the angular rate vector[3,5,9,11],

(21)

wheregiis a coefficient vector;Qis the number of coefficient vectors;t0is the beginning time measured. Integrating Eq.(21) fromtl-1tot, we obtain

(22)

Eqs.(21) and (22) are substituted into Eq.(1). After integrating and simplifying withtl-1=tl-Tl=tl-LTkandt0=0, we can give the analytical coning correction δφl,

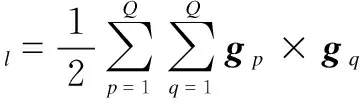
(23)

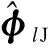
(24)

2.3 Algorithm example

The coning correction forms expressed by Eqs.(3) and (4) can be also, respectively, rewritten as

(25)

(26)

Using Eq.(18), we can design the coefficientsJss for anyN-sample algorithm. WhenL=N=4, the new 4-sample algorithm becomes

(27)

In addition, the coning coefficientsKss in Eq.(25) are designed by the same optimization method as given in the above. WhenL=N=4, the traditional 4-sample algorithm[3]becomes

(28)

3 Simulation

To illustrate the properties of two 4-sample coning algorithms, algorithm errors are computed under coning environments and maneuver environments, and then algorithm performances are compared and analyzed. In each algorithm,Tk=1 ms,Tl=LTk, andL=N=4.

In Fig.1, CFSn4 indicates the 4-sample coning algorithm based on Eq.(4) taking the coefficients determined by the coning frequency Taylor series method. CFSc4 represents the 4-sample coning algorithm based on Eq.(3) taking the coefficients determined by the coning frequency Taylor series method.

Fig.1 Normalized average rotation error rate (β) and vs. coning frequency β/(2πTk)

For algorithm performance evaluation, we set

Q=5

Then the extreme 2 s angular maneuver rate profile is given in Fig.2.

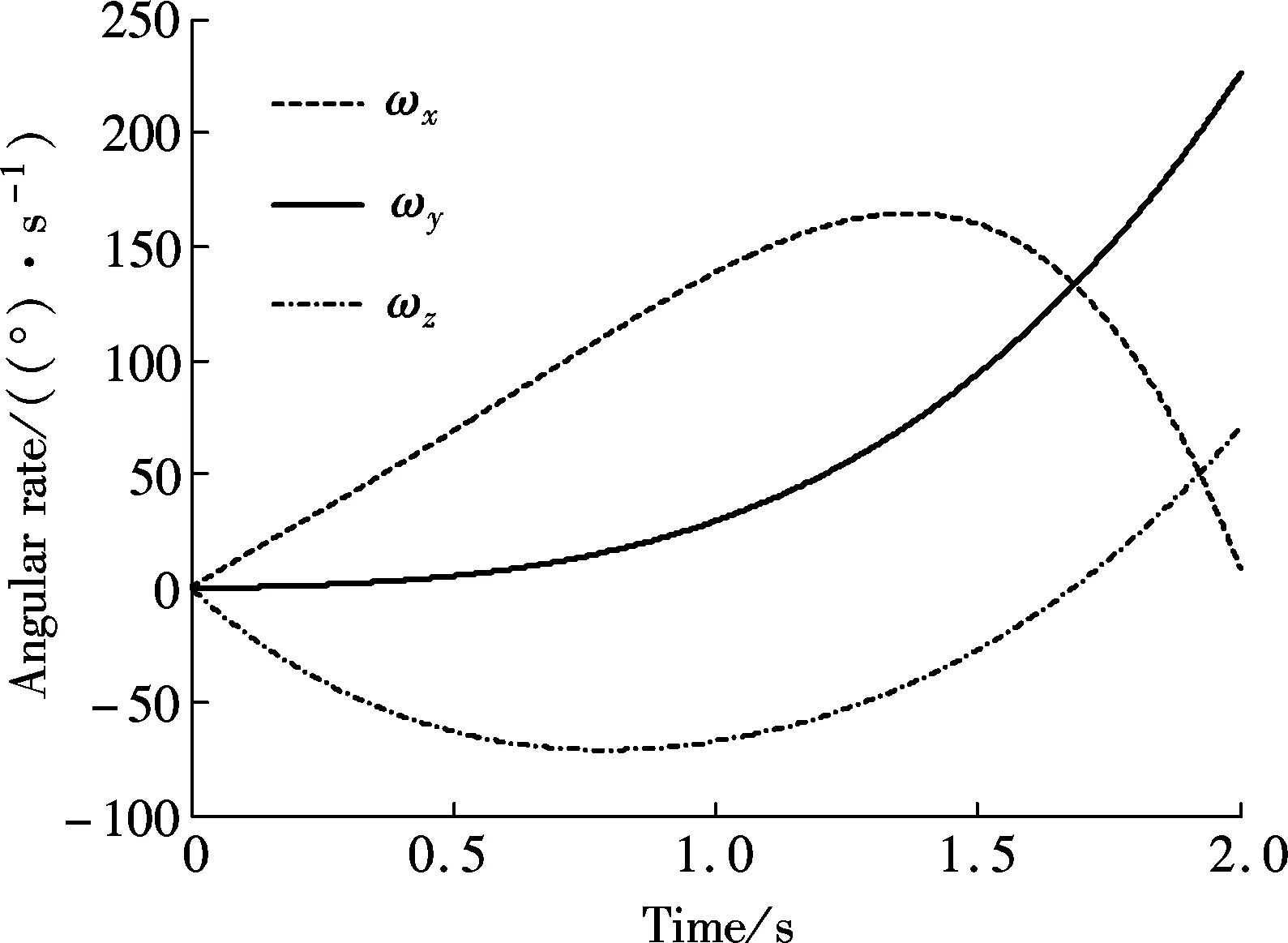
Fig.2 Maneuver angular rate vs. time

Fig.1 indicates that the new 4-sample coning algorithm CFSn4 and the traditional compressed 4-sample coning algorithm CFSc4, both with the coefficients optimized by using the coning frequency Taylor series method, have the same algorithm accuracy over the coning frequency range. It means that both algorithms are equivalent. This is because the new coning correction form defined by Eq.(4) and the traditional compressed coning correction form defined by Eq.(3) are both based on the coning motion properties and derived from the uncompressed form defined by Eq.(2).

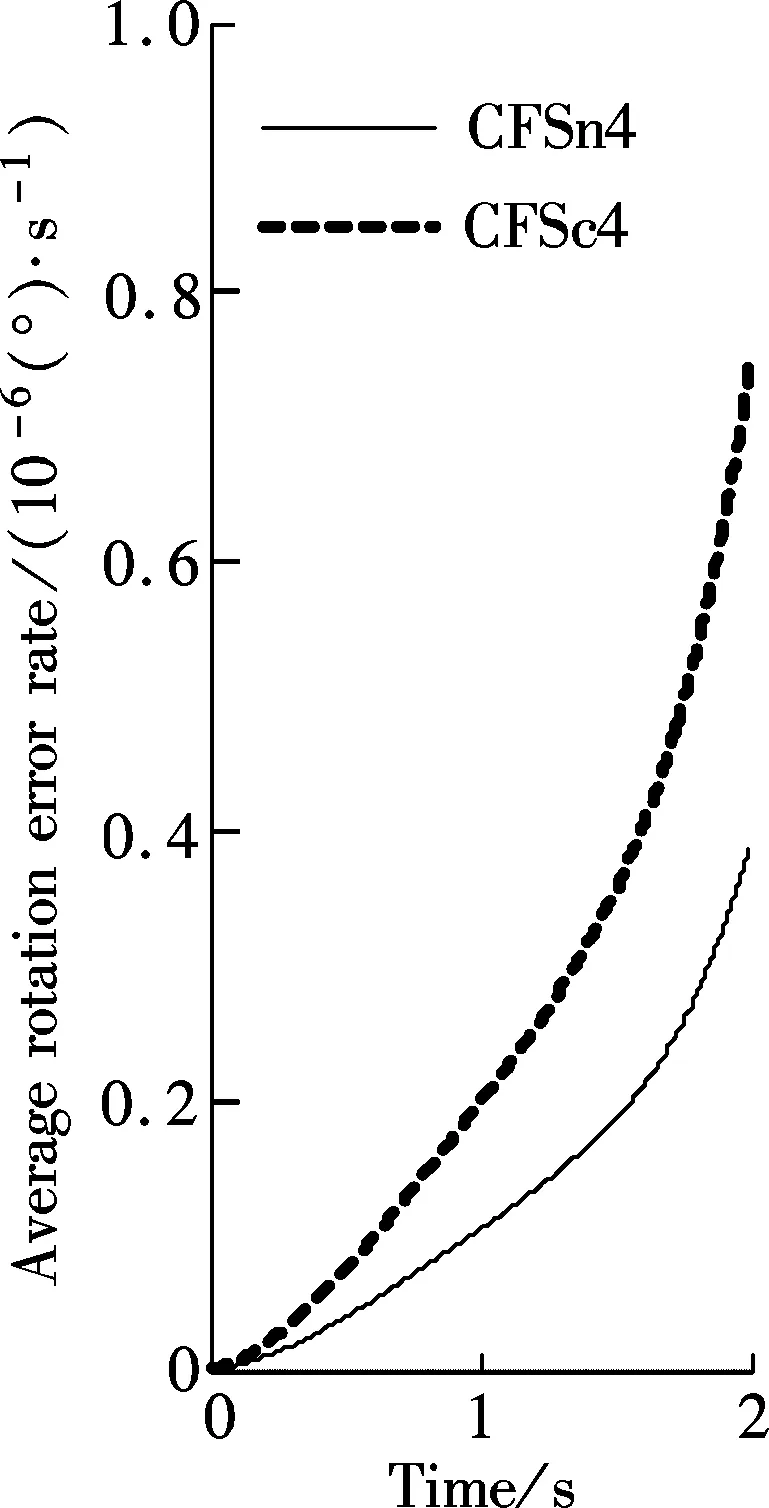
By comparing algorithm errors in the set maneuver environment, Fig.3 illustrates that the maneuver error of the new 4-sample coning algorithm CFSn4 approaches half that of the traditional compressed 4-sample coning algorithm CFSc4. For example, the maximum of thez-component of the maneuver error vector, as the maximum of three components of the error vector for the algorithm CFSn4, is approximately 2.2×10-6(°)/s (about 7.92×10-3(°)/h) and lies at 2 s, and that for the algorithm CFSc4 is approximately 4.2×10-6(°)/s (about 1.512×10-2(°)/h) and also lies at 2 s. It means that for a typical aircraft INS with a 0.01 (°)/h gyro error, the accuracy improvement of the algorithm CFSn4 is significant compared to the algorithm CFSc4 and can evidently improve the INS performance in maneuver environments.

(a) (b) (c)

4 Conclusion

The proposed coning correction algorithm is efficient in coning environments and maneuver environments. The new coning algorithm and the traditional compressed coning algorithm have the same efficiency with the same computation load and coning accuracy. In maneuver environments, the performance of the proposed algorithm is clearly superior to that of the traditional compressed algorithm. The new 4-sample coning algorithm almost doubles in maneuver accuracy, compared to the traditional compressed 4-sample coning algorithm. The proposed algorithm has improved maneuver accuracy while maintaining coning accuracy and algorithm throughput.

[1]Miller R B. A new strapdown attitude algorithm [J].JournalofGuidance,Control,andDynamics, 1983, 6(4): 287-291.

[2]Lee J G, Mark J G, Tazartes D A, et al. Extension of strapdown attitude algorithm for high-frequency base motion [J].JournalofGuidance,Control,andDynamics, 1990, 13(4): 738-743.

[3]Ignagni M B. Efficient class of optimized coning compensation algorithms [J].JournalofGuidance,Control,andDynamics, 1996, 19(2): 424-429.

[4]Mark J G, Tazartes D A. Tuning of coning algorithms to gyro data frequency response characteristics [J].JournalofGuidance,Control,andDynamics, 2001, 24(4): 641-647.

[5]Savage P G. Coning algorithm design by explicit frequency shaping [J].JournalofGuidance,Control,andDynamics, 2010, 33(4): 1123-1132.

[6]Savage P G. Explicit frequency shaped coning algorithms for pseudoconing environments [J].JournalofGuidance,Control,andDynamics, 2011, 34(3): 774-782.

[7]Tang C Y, Chen X Y, Li J L. Coning algorithm design for angular rate inputs [J].JournalofChineseInertialTechnology, 2013, 21(4): 456-461. (in Chinese)

[8]Tang C Y, Chen X Y. An angular rate input attitude algorithm in SINS [J].JournalofSoutheastUniversity:NaturalScienceEdition, 2014, 44(3): 544-549. (in Chinese)

[9]Tang C Y, Chen X Y. A generalized coning correction structure for attitude algorithms [J].MathematicalProblemsinEngineering, 2014, 2014: 1-15.

[10]Chen J F, Chen X Y, Zhu X F. An improved coning algorithm based on second optimization [J].JournalofChineseInertialTechnology, 2012, 20(2): 131-135. (in Chinese)

[11]Song M, Wu W Q, Pan X F. Approach to recovering maneuver accuracy in classical coning algorithms [J].JournalofGuidance,Control,andDynamics, 2013, 36(6): 1872-1881.

[12]Tang C Y, Chen X Y. A class of coning algorithms based on a half-compressed structure [J].Sensors, 2014, 14(8): 14289-14301.

一種提升圓錐算法機(jī)動(dòng)性能的方法

湯傳業(yè) 陳熙源 宋 銳

(東南大學(xué)儀器科學(xué)與工程學(xué)院, 南京 210096)(東南大學(xué)微慣性儀表與先進(jìn)導(dǎo)航技術(shù)教育部重點(diǎn)實(shí)驗(yàn)室, 南京 210096)

為提高捷聯(lián)慣導(dǎo)姿態(tài)圓錐算法的機(jī)動(dòng)性能,提出一種新的圓錐補(bǔ)償結(jié)構(gòu)，該結(jié)構(gòu)通過在傳統(tǒng)結(jié)構(gòu)中增加一個(gè)子樣獲得.在給出經(jīng)典圓錐運(yùn)動(dòng)定義的基礎(chǔ)上,推導(dǎo)了基于新的圓錐補(bǔ)償結(jié)構(gòu)的圓錐補(bǔ)償殘余誤差通式,并采用頻率泰勒方法設(shè)計(jì)了新的圓錐補(bǔ)償結(jié)構(gòu)系數(shù),從而獲得一類新的圓錐補(bǔ)償算法.定義了2種圓錐算法誤差模型,分別用于圓錐環(huán)境和機(jī)動(dòng)環(huán)境下的圓錐算法性能評(píng)估.仿真結(jié)果表明:新的四子樣圓錐算法的機(jī)動(dòng)精度比傳統(tǒng)四子樣圓錐算法的機(jī)動(dòng)精度提高約1倍;與傳統(tǒng)的壓縮圓錐算法相比,新的圓錐算法在保持圓錐性能的同時(shí)具有更好的機(jī)動(dòng)性能.

圓錐算法;圓錐補(bǔ)償結(jié)構(gòu);機(jī)動(dòng)性能;圓錐性能;頻率泰勒方法

V241.6

Received 2014-05-06.

Biographies：Tang Chuanye (1982—), male, graduate; Chen Xiyuan (corresponding author), male, doctor, professor, chxiyuan@seu.edu.cn.

s：The National Natural Science Foundation of China (No.51375087), the Specialized Research Fund for the Doctoral Program of Higher Education (No.20110092110039), the Public Science and Technology Research Funds Projects of Ocean (No.201205035), the Scientific Innovation Research of College Graduates in Jiangsu Province (No.CXZZ12_0097), the Scientific Research Foundation of Graduate School of Southeast University (No.YBJJ1349).

：Tang Chuanye, Chen Xiyuan, Song Rui. An approach to improving maneuver performance of coning algorithm[J].Journal of Southeast University (English Edition),2014,30(4):439-444.

10.3969/j.issn.1003-7985.2014.04.007

10.3969/j.issn.1003-7985.2014.04.007