Influence of bending rigidity of submerged vegetation on local flow resistance*
WU Long-hua (吳龍華), YANG Xiao-li (楊校禮)
College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China, E-mail: jxbywlh2000@aliyun.com
Influence of bending rigidity of submerged vegetation on local flow resistance*
WU Long-hua (吳龍華), YANG Xiao-li (楊校禮)
College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China, E-mail: jxbywlh2000@aliyun.com
(Received May 7, 2013, Revised December 17, 2013)
The different state of the submerged vegetation has different influences on the flow resistance. This paper explores the relationship between the state and the resistance of an individual submerged vegetation, and the relative bending rigidity of the submerged vegetation is determined by the state of the submerged vegetation. Based on the experimental observations, the state and the resistance of an individual submerged vegetation are analyzed under different inflow conditions. At the same time, the influences of the various submerged vegetations on the flow resistance are discussed under the same inflow conditions. Some interesting relationships are obtained between the flow resistance and the relative bending rigidity of the submerged vegetation, and it is shown that the flow resistance increases with the increase of the relative bending rigidity of the submerged vegetation, and they are positively correlated.
individual submerged vegetation, relative bending rigidity, local flow resistance
Introduction
Aquatic vegetations are usually found in the downstream riverbank of natural rivers, as an important part of a river ecosystem. The aquatic plant has important ecological and environmental functions, such as protecting soil, preventing soil erosion, restoring water eco-environment and providing nutritive materials for the river ecosystem[1-3]. These aquatic plants can affect the velocity, the current direction, the internal flow structure, and the sediment transport of the local flow field to a certain extent, and increase the roughness of the river bank[4-8]. The aquatic plant becomes one of important factors for the flood control, and the local resistance of the submerged vegetation becomes one of the important concerns of the river management.
The flows with vegetations were widely studied by experiments and theoretical analyses. White and Nepf[9]studied the vegetative drag in a partially vegetated shallow channel. Righetti and Armanini[10]studied the flow resistance in open channel flows with sparsely distributed bushes. The vertical profiles, the relative shear velocities, and the Manning roughness coefficients were studied under different inflow conditions and aquatic vegetation densities by experiment observations[11]. Velasco et al.[12]observed the resistance and turbulent characteristics of the flexible vegetation of different plant densities in flume experiments. Carollo et al. deduced a flow resistance equation based on flow velocity measurements in vegetated channels[13,14]. Wu[15]analyzed the flow resistance factors of non-submerged rigid vegetations in open channels. Liu et al.[5]evaluated the characteristics of secondary flows in compound channels with vegetated floodplains in a rectangular vegetated laboratory flume. Leek et al.[16]analyzed the drag coefficients of the saw grass in the Florida Everglades. Juha[17]investigated the flow structure and the resistance of submerged flexible vegetations by flume experiments.
As stated above, the researches of the flow resistance almost always aimed at some state of the aquatic vegetation. It is shown that the aquatic vegetation has three different states with different inflow conditions, and they are the almost entirely bending state, the waggling state and the perpendicular state, respectively[18,19]. When the aquatic vegetation is in different states, the flow resistance of the aquatic vegetationis quite different. However, the vegetation on floodplains is commonly assumed to behave as rigid roughness, and it can lead to large errors in the relationships between the velocity and the drag force[20]. So, in this paper, based on the author’s previous researches, the flow resistance of an individual submerged vegetation is analyzed in three different states, and the influence mechanisms of the flow resistance are discussed with respect to the relative bending rigidity of the individual submerged vegetation by analyzing the experimental data.
1. Theoretical considerations
Figure 1 gives a force analysis of the control volume (the part between section 1 and section 2), where h1and h2are the flow depths at the two sections, respectively, Δl the length of the control volume in the flow direction, i is the bottom slope, Fgis the gravity of the control volume in the X direction, 1P and 2P are the dynamic pressure forces at the upstream and the downstream of the control volume, respectively, FVis the resistance of the flow by the vegetation, and Fsis the shear force on the bottom.

Fig.1 Force analysis of control volume
For a uniform flow, the force balance equation along the X direction can be written as

The gravity of the control volume can be expressed as

where ρ is the density of water, g is the acceleration of gravity, h( x) is the water depth, as a function of distance x, B is the width of the section, which is assumed to be constant, and Δl is the distance between the sections 1 and 2.
The dynamic pressure forces can be calculated as

where1P and2P are the pressures at sections 1 and 2 of the control volume, respectively.
Normally, the drag force of the individual submerged vegetation can be described as:

where CDis the dimensionless drag coefficient, V is the velocity of the inflow, HVis the height of the submerged vegetation, and W is the projection width of the submerged vegetation in the normal direction of flow.
Generally, the total shear force can be expressed as

where S is the corresponding wetted perimeter, 0τ is the shear stress on the boundary of the control volume, which could be expressed as

where J is the hydraulic grade, A is the wetted cross-sectional area of a river.
In this paper, Δl is treated as a unit-distance, and the water depth remains unchanged at this distance. If the wall surface is smooth, the total shear force is far less than the resistance of the submerged vegetation in this distance, and can be neglected.
Then, Eqs.(1) and (2) can be rewritten as, respectively:

where H0is the water depth of the control volume.
Substituting Eqs.(4) and (8) into Eq.(7) leads to
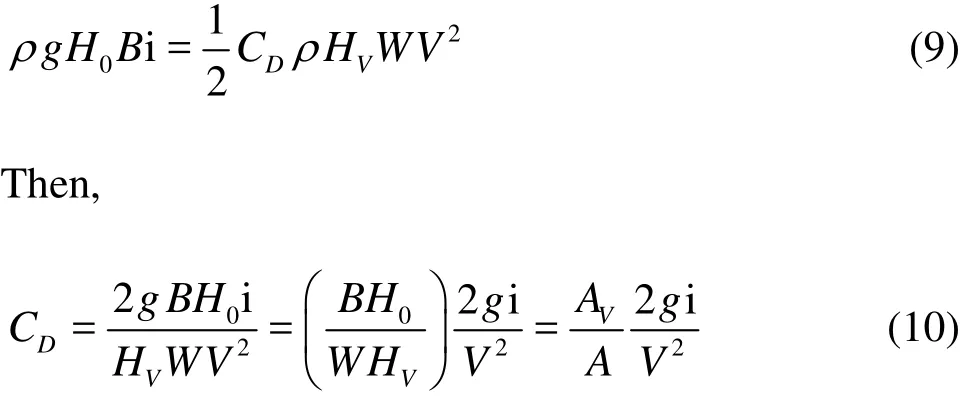
where AVis the projection area of the submerged vegetation in the normal direction of a flow.
In an engineering application, the flow drag is conveniently specified by the roughness coefficient. Using Manning’s and Chezy’s formulas for Eq.(10), the roughness coefficient is expressed as
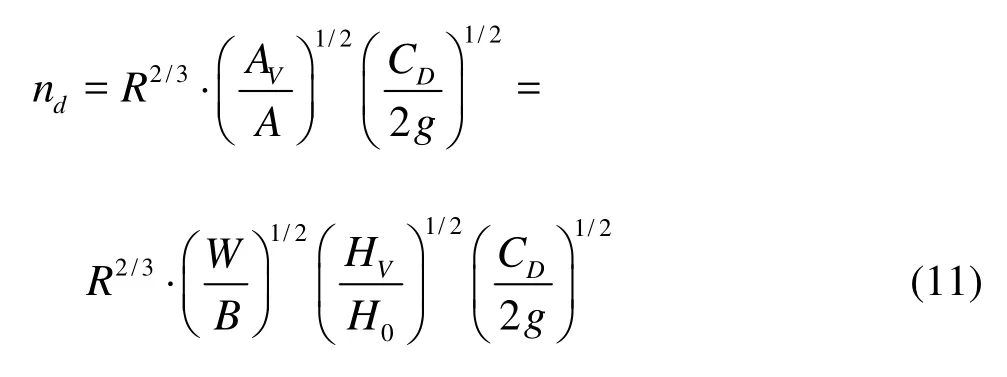
where R is the hydraulic radius.
Equation (11) shows that the roughness coefficient ndhas a positive exponential correlation with the drag coefficient CDand the projection area AVof the submerged vegetation in the normal direction of the flow. In other words, the resistance of the submerged vegetation has a positive exponential correlation with the relative projection area of the vegetation in the vertical direction (AV/A). With the wetted cross-sectional area fixed, the resistance increases with the increase of the projection area of the vegetation (AV). Further analysis indicates that, the roughness coefficient is closely related to the relative height (HV/H0) and the relative weight (W/ B) of the submerged vegetation. Equation (11) shows that the roughness coefficient decreases with the decrease of the relative height (HV/H0), which means that the roughness coefficient of the submerged vegetation decreases with the increase of the water depth. When the water depth reaches a certain height, the roughness coefficient of the submerged vegetation will become smaller, and may be neglected, as in good agreement with the previous researches[13]. In the following parts, the drag coefficient (CD) of the individual submerged vegetation will be investigated by a series of experiments.
2. Experimental procedures
2.1 Simulation of submerged vegetation
The caudex of the submerged vegetation projection in the flow direction is a rectangle. Then, the plexiglass flake is used to simulate the caudex in the experiments, and the cross section of the plexiglass is shown in Fig.2, in which W is the width, T is the thickness, and HVis the height of the flake.


where E is the elastic modulus of the submerged vegetation, μ is the coefficient of the dynamic viscosity, V is the inflow velocity, which can be substituted by the averaged velocity of the cross section; and I is the moment of inertia with respect to the neutral axis, which can be determined from

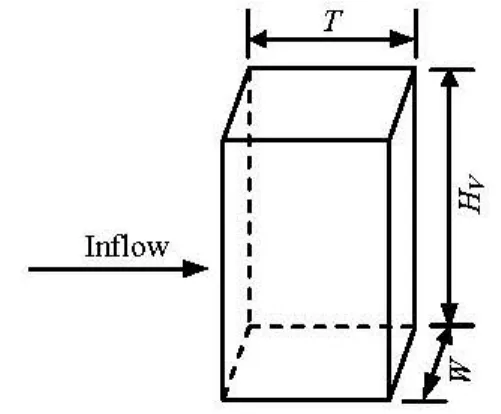
Fig.2 Sketch of plexiglass flake
In order to control the measurement precision, the resistance of the individual submerged vegetation is amplified. The width of the flakes is 0.05 m in these experiments, and the six thicknesses, including 5× 10-4m, 7×10-4m, 1.4×10-3m, 2.0×10-3m, 2.5× 10-3m and 4.6×10-3m, are considered to simulate different rigidities of the submerged vegetation.
2.2 Experimental setup and conditions
The experiments were conducted in the Engineering Hydrodynamics Laboratory of Hohai University. The experimental setup is a self-circulation water system, and it consists of pump, inlet, static pond, energy dissipation grid, tail gate, measuring weir and recycling tank (Fig.3(a)), as well as a glass flume. The glass flume is a smooth glass rectangular open-channel of 10.00 m long, 0.30 m wide and 0.45 m deep. In this experiment, the bed slope of the flume can be adjusted to form a steady uniform flow. The submerged vegetation is located in the central part of the cross section of the glass flume, as shown in Fig.3(b), in which x, y and z denote the longitudinal, transverse and vertical axes, respectively.
In these experiments, the flow discharge is adjusted by the water pump. To keep the water flow stable, the water needs to flow through the static pond and the energy dissipation grid. The discharge is measured by the right angled thin triangular weir with accuracyof 1%. The water depth of the flume is adjusted by the tail gate installed at the end of the flume, and the water level is measured by an exploring tube with the precision of 0.0001 m.

Fig.3 Sketch of experimental setup

Table 1 Experimental conditions for the runs considered
Multi-cases were considered for different cross sections of the submerged vegetation. These different cross sections of the plexiglass flake can be used to simulate a variety or the growing season of the submerged vegetation. These experiments were conducted by changing the water depth and the flow discharge. The main experimental parameters of every case are shown in Table 1.
3. Experimental results and analyses
Based on the experimental results, the drag coefficient (CD) and the relative bending rigidity of submerged vegetation (RJ) are calculated by Eqs.(10) and (12) in Sections 1 and 2. Three different states of the submerged vegetation are observed under various inflow conditions, and they are the almost entirely bending state, the waggling state and the perpendicular state. The each critical relative bending rigidity of the individual submerged vegetation is determined for the three states of the submerged vegetation by Wu et al.[23], and they are shown as follows:
If lg(RJ)<2.60, the submerged vegetation could be considered as complete flexible, otherwise, it is non-flexible.
If lg(RJ)≥4.27, the submerged vegetation could be considered as complete rigid.
When 2.60<lg(RJ)<4.27, the submerged vegetation is in a state of waggle.
Then, the flow resistance of the individual submerged vegetation will be analyzed under different states in the following paragraphs.

Fig.4 Relations between lg(RJ) and V
3.1 Relative bending rigidity characteristics
Figure 4 shows the variation of lg(RJ) with V under different inflow conditions.
It can be seen that the relative bending rigidity of the submerged vegetation decreases with the increase of the mean velocity of the inflow. When the thickness of the flake (T) is 0.0005 m, the submerged vegetation is always in an almost entirely bending (i.e., complete flexible) state under the experimental conditions. When T=1.4×10-3m or 2×10-3m, the submerged vegetation always keeps in the waggle state. When T=7×10-4m, the states of the submerged vegetation are varied according to the inflow velocity, the state of submerged vegetation is changed from the waggling state to the almost entirely bending state with the inflow velocity increasing. When T=2.5× 10-3m, the states of the submerged vegetation are varied according to the inflow velocity too, the state of the submerged vegetation is changed from the perpendicular (complete rigid) state to the waggling state with the inflow velocity increasing. When T=4.6× 10-3m, the submerged vegetation is always in a perpendicular (i.e., complete rigid) state under the experimental conditions. Above result shows that the state of the submerged vegetation is not immutable, but changes with the inflow conditions.
3.2 Resistance under different states
Figure 4 shows that the state of the individual submerged vegetation changes with the inflow conditions. In the experimental conditions, when T= 0.005 m, T=0.0014 m or 0.002 m and T=0.0046 m, the submerged vegetation remains their own states unchanged, respectively. For different inflow conditions, the drag coefficient (CD) of the different state of the submerged vegetation and the relative bending rigidity of the submerged vegetation (RJ) are shown in Fig.5.

Fig.5 Relationship between CDand lg(RJ) in different states
Figure 5 shows that the drag coefficient (CD) increases with the increase of the relative bending rigidity (RJ) for every state of the submerged vegetation. The relative bending rigidity of the submerged vegetation reflects the ability of bending under the current action, and the larger its value, the smaller the bending of the submerged vegetation. That means that the effe-ctive projection area of the vegetation in the normal direction of flow is increased. So, the larger the relative bending rigidity of the submerged vegetation, the larger he flow resistance.
The relationships between the relative bending rigidity of the submerged vegetation and the drag coefficient (CD) are determined as follows:
Perpendicularity state

where R2is the correlation coefficient of the above fitting equations, which shows the accuracy of the expression.
Equations (14)-(17) show that the relation between the drag coefficient (CD) and the denary logarithm of RJis a positive linear correlation. For different states of the submerged vegetation, the relationships between lg(RJ) and CDcan be expressed in a unified form as

where C1and C0are the dimensionless integration constants.
It can be concluded that the flow resistance is in a positive correlation with the relative bending rigidity of the submerged vegetation in each state.
3.3 Impact of various states
Under the same inflow conditions, the submerged vegetation state is also varied with the vegetation variety and the growing season. This change of state of the submerged vegetation is observed experimentally. In different experimental conditions, the drag coefficient (CD) of different submerged vegetation types is shown in Figs.6(a)-6(e), respectively.

Fig.6 Drag force coefficient changes with submerged vegetation types
It can be seen from Fig.6 that the drag coefficient (CD) increases with the increase of the relative bending rigidity of the submerged vegetation (RJ). When the submerged vegetation is still in the almost entirely over or waggle state (i.e., not in the perpendicular state), the flow resistance of the submerged vegetation is rapidly increased if the relative bending rigidity of the submerged vegetation increases. As thecomplete rigid state is reached, the growth trend of the resistance of the submerged vegetation is slow. Accordingly, the resistance is reduced when the relative bending rigidity of the submerged vegetation decreases. That pattern is particularly obvious in a state other than the perpendicular state of the submerged vegetation. The primary cause for the difference is due to the effective projection area change resulted from the state transition of the submerged vegetation. From the almost entirely bending state to the waggling state and then to the perpendicular state, the effective projection area of the submerged vegetation increases. When the state of the submerged vegetation changes from the almost entirely bending state to the waggling state, the change rate of the effective projection area is larger than that from the waggling state to the perpendicular state of the submerged vegetation.
In extremes, the submerged vegetation is completely flattened under the current action, and it is parallel to the flow directions. Now the counterforce of the submerged vegetation to the flow largely disappears, the resistance of the submerged vegetation is very small, and it just changes the local friction of flow. On the other hand, when the state of the submerged vegetation always keeps perpendicular (i.e., complete rigid), and it is perpendicular to the flow directions. Then the effective projection area of the submerged vegetation in the normal direction of flow is the largest, which means that the resistance of the submerged vegetation is the largest at the same time. Under such circumstances, the flow resistance of the submerged vegetation is only related to the inflow conditions, and it is independent of the bending rigidity of the submerged vegetation. Because of the restriction of experimental conditions, the resistance of the submerged vegetation tends towards stability under the complete perpendicular state.
4. Conclusions
For different states of the submerged vegetation, the influences of the individual submerged vegetation on the flow resistance are studied in this paper. The following conclusions are drawn:
(1) Because of the vegetation variety and the growing season of the submerged vegetation, its bending rigidity is different. The submerged vegetation has different states under the same inflow conditions. On the other hand, the state of the same submerged vegetation is varied with different inflow conditions.
(2) In case of the completely non-rigid state, the flow resistance of the submerged vegetation is rapidly increased while the relative bending rigidity of the submerged vegetation increases. As the complete rigid state is reached, the growth trend of the resistance of the submerged vegetation is slow. The primary cause for the difference is due to the effective projection area changes resulted from the state transition of the submerged vegetation. When the state of the submerged vegetation always keeps perpendicular, the flow resistance of the submerged vegetation is only related to the inflow conditions, and it is independent of the bending rigidity of the submerged vegetation.
(3) Especially, when the state of the submerged vegetation always keeps perpendicular (i.e., complete rigid), the flow resistance increases with the increase of the relative bending rigidity for every state of the submerged vegetation, and the relation between them is a positive correlation. In this paper, the quantitative relationship between the flow resistance and the relative bending rigidity of the submerged vegetation is not defined for the individual submerged vegetation. In the future research, the relative bending rigidity of the submerged vegetation, the inflow condition, the bending of the submerged vegetation, and the flow resistance will be further explored, and the quantitative relationship among the relative bending rigidity of the submerged vegetation, the bending of the submerged vegetation and the flow resistance will be studied.
[1] YANG Ming, WU Xiao-gang and ZHANG Wei-hao et al. Application of aquatic plant in ecological restoration of eutrophic water[J].Environmental Science and Technology,2007, 30(7): 98-102(in Chinese).
[2] YUJI T., SYUNSUKE I. and KENTARO K. et al. Effects of flood flow on flood plain soil and riparian vegetation in a gravel river[J].Journal of Hydraulic En-gineering, ASCE,2005, 131(11): 950-960.
[3] WU Zhen-bin, QIU Dong-ru and HE Feng et al. Effects of rehabilitation of submerged macrophytes on nutrient level of a eutrophic lake[J].Chinese Journal of App-lied Ecology,2003, 14(8): 1351-1353(in Chinese).
[4] MUSLESH F. A., CRUISE J. F. Functional relationships of resistance in wide flood plains with rigid unsubmerged vegetation[J].Journal of Hydraulic Enginee-ring,2006,132(2): 163-171.
[5] LIU Chao, SHAN Yu-qi and YANG Ke-jun et al. The characteristics of secondary flows in compound channels with vegetated floodplains[J].Journal of Hydrody-namics,2013, 25(3): 422-429.
[6] SHI Zhong, LI Yan-hong. Experimental studies of mean velocity profiles in vegetated river flow[J].Journal of Shanghai Jiaotong University, ASCE,2003, 37(8): 1254- 1260(in Chinese).
[7] TSIHRINTZIS V. A. Discussion of “Variation of roughness coefficients for unsubmerged and submerged vegetation”[J].Journal of Hydraulic Engineering,ASCE,2001, 127(3): 241-244.
[8] MUSLESH F. A., CRUISE J. F. Functional relationships of resistance in wide flood plains with rigid unsubmerged vegetation[J].Journal of Hydraulic Enginee-ring, ASCE,2006,132(2): 163-171.
[9] WHITE B. L., NEPF H. M. A vortex-based model of velocity and shear stress in a partially vegetated shallow channel[J].Water Resources Research,2008, 44(1): W01412.
[10] RIGHETTI M., ARMANINI A. Flow resistance in open channel flows with sparsely distributed bushes[J].Jour-nal of Hydrology,2002, 269(1-2): 55-64.
[11] HUI Er-qing, JIANG Chun-bo and PAN Ying-wang. Vertical velocity distribution of longitudinal flow in a vegetated channel[J].Journal of Tsinghua University (Science and Technology),2009, 49(6): 834-837(in Chinese).
[12] VELASCO D., BATEMAN A. and REDONDO J. M. et al. An open channel flow experimental and theoretical study of resistance and turbulent characterization over flexible vegetated linings[J].Flow, Turbulence andCombustion,2003, 70(1-4): 69-88.
[13] CAROLLO F. G., FERRO V. and TERMINI D. Flow velocity measurement in vegetated channels[J].Journal of Hydraulic Engineering, ASCE,2002, 128(7): 664- 673.
[14] CAROLLO F. G., FERRO V. and TERMINI D. Flow resistance law in channels with flexible submerged vegetation[J].Journal of Hydraulic Engineering, ASCE,2005, 131(7): 554-564.
[15] WU Fu-sheng. Turbulent characteristics of flow on floodplains and wetlands with flexible vegetations[J].Journal of Hydraulic Engineering,2007, 38(11): 1301-1305(in Chinese).
[16] LEE K. L., ROIG L. C. and JENTER H. L. et al. Drag coefficients for modeling flow through emergent vegetation in the Florida Everglades[J].Ecological Enginee-ring,2004, 22(4-5): 237-248.
[17] JUHA J. Effect of submerged flexible vegetation on flow structure and resistance[J].Journal of Hydrology,2005, 307(1-4): 233-241.
[18] SAMANI J. M. V., KOUWEN N. Stability and erosion in grassed channels[J].Journal of Hydraulic Enginee-ring, ASCE,2002, 128(1): 40-45.
[19] WU Long-hua, YANG Xiao-li. Factors influencing bending rigidity of submerged vegetation[J].Journal ofHydrodynamics,2011, 23(6): 723-729.
[20] NIKORA V., LARNED S. and NIKORA N. et al. Hydraulic resistance due to aquatic vegetation in small streams: Field study[J].Journal of Hydraulic Engineering, ASCE,2008, 134(9): 1326-1332.
10.1016/S1001-6058(14)60027-5
* Project supported by the National Natural Science Foundation of China (Grant No. 51179057).
Biography: WU Long-hua (1974- ), Male, Ph. D., Associate Professor
- 水動力學(xué)研究與進(jìn)展 B輯的其它文章
- Numerical prediction of 3-D periodic flow unsteadiness in a centrifugal pump under part-load condition*
- Experimental investigations of transient pressure variations in a high head model Francis turbine during start-up and shutdown*
- Improved conservative level set method for free surface flow simulation*
- Capillary effect on the sloshing of a fluid in a rectangular tank submitted to sinusoidal vertical dynamical excitation*
- Effect of compressive stress on the dispersion relation of the flexural–gravity waves in a two-layer fluid with a uniform current*
- Comprehensive analysis on the sediment siltation in the upper reach of the deepwater navigation channel in the Yangtze Estuary*

