金興華

(上海商學院 數(shù)學系,上海 200235)

0 引 言

早期宇宙的相變能產(chǎn)生各種拓撲缺陷,這些拓撲缺陷在宇宙學中有很重要的意義[1].整體單極子是最重要的缺陷之一.Barriola和Vilenkin[2]首先研究了整體單極子的引力效應.當考慮引力時,整體單極子的線性發(fā)散質量有一個效果,這個效果類似于一個欠缺角.Harari 和Loust`o[3],還有史和李[4]已經(jīng)表明,這個小引力勢實際上是排斥的.在FRW 時空中,拓撲缺陷也已被研究過了[5-7].在漸近dS/AdS時空[8-9]和Brans-Dicke 理論下[10]的整體單極子的性質被發(fā)現(xiàn)和通常的單極子有很大的不同.如果將非正則動能相引入到整體單極子,金等[11]發(fā)現(xiàn)引力場可能是吸引的,也可能是排斥的,這依賴于不同的非正則動能項.劉等[12]已探討過Dirac-Born-Infeld 整體單極子的自引力問題.

歷史上,為了解決庫侖場和點粒子自能的發(fā)散問題,Born和Infeld[13]將行列式形式引入作用量.1924年,Eddington[14]提出了一個不同與廣義相對論的引力理論,行列式形式出現(xiàn)在了作用量中,他認為基本場應該是聯(lián)絡.對該作用量進行變分可以得到等效的愛因斯坦方程.但是該理論并不完備,因為它不包含物質部分.最近,Banados 和Ferreira 基于Eddington 的理論,提出了一個改進的引力理論,通常稱為Eddington-inspired Born-Infeld(簡記EiBI)引力[15].該理論的作用量可以包含物質部分,它彌補了Eddington 引力理論中的問題.為了克服高階導數(shù)和ghost帶來的問題,EiBI引力采用的是Palatini形式,即將度規(guī)和聯(lián)絡處理為獨立的場.

EiBI引力是非常吸引人的,因為在真空的情況下,它可以退化為廣義相對論,并且可以避開大爆炸理論和恒星引力塌縮過程中的奇點問題.但是,EiBI引力理論也存在問題.例如,在多方星的表面存在曲率奇點[16].類似的奇性也存在于恒星內部的相變過程[17].最近,有研究認為恒星表面的奇點問題可以被克服[18].

本文作者基于EiBI引力理論,導出整體EiBI-單極子的方程,并給出參數(shù)κ很小時方程的漸近形式,進一步討論了整體EiBI-單極子在無窮遠處的級數(shù)解.

1 EiBI引力理論

整個討論過程中,單位取c=G=1.EiBI引力理論的作用量為:

(1)

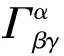
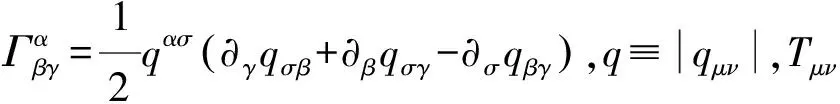
2 整體EiBI-單極子

彎曲時空中引力的整體EiBI-單極子的作用量為:

(4)

其中σ0是一個以質量為單位的對稱破缺標度.描寫整體EiBI-單極子的刺猬構形為:

(5)

其中xaxa=ρ2,a=1,2,3,如果在空間無窮遠處h→1,將得到一個整體EiBI-單極子解.

在靜態(tài)球對稱時空中,時空度規(guī)gμν和輔助度規(guī)qμν采用如下形式:

其中 dΩ2=dθ2+sin2θdφ2.引入無量綱參數(shù)r=σ0ρ,由方程(4)和(5),可以得到關于h的運動方程:

(8)

其中,撇表示對r求導.由方程(3),可以得到關系:

(9)

其中

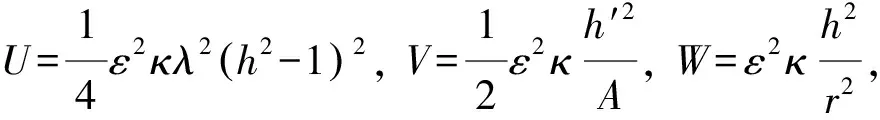
由方程(2)可以得到兩個獨立的方程:

(10)

(11)

當|κ|?1,可以得到方程(8),(10)和(11)關于κ的漸近形式:

(12)

(13)

(14)

其中

容易發(fā)現(xiàn),當|κ|→0時,這些方程可以恢復到標準的整體單極子方程.

在r?1區(qū)域,可以展開h(r),A(r),B(r),f(r)得

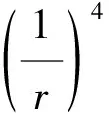
(19)

由此,ε2描寫時空的一個立體欠缺角.

為了顯示立體欠缺角的效果,研究整體EiBI-單極子周圍測試粒子的運動.為求解測地線方程,引入一個無量綱量u=GM∞/r,于是可以得到u關于φ的二階微分方程

(20)

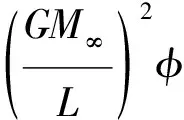
(21)

其中e表示偏心率.當一個測試粒子繞整體EiBI-單極子轉一圈時,它的進動是:

(22)

相比正常星的進動情況,方程(22)的最后一項是修正項.

參考文獻:

[1] VILENKIN A,SHELLARD E P S.Cosmic Strings and Other Topological Defects[M].Cambridge:Cambridge Unversity Press,1994.

[2] BARRIOLA M,VILENKIN A.Gravitational field of a global monopole[J].Phys Rev Lett,1989,63:341-348.

[3] HARARI D,LOUSTO C.Repulsive gravitational effects of global monopoles[J].Phys Rev D,1990,42:2626-2631.

[4] SHI X,LI X Z.The gravitational field of a global monopole[J].Class Quantum Grav,1991,8:761-767.

[5] BASU R,GUTH A H,VILENKIN A.Quantum creation of topological defects during inflation[J].Phys Rev D,1991,44:340-351.

[6] BASU R,VILENKIN A.Evolution of topological defects during inflation[J].Phys Rev D,1994,50:7150-7153.

[7] CHEN C,CHENG H,LI X Z,ZHAI X H.Non-existence of topological defects during inflation beyond the critical value[J].Class Quantum Grav,1996,13:701-704.

[8] LI X Z,HAO J G.Global monopole in asymptotically dS/AdS space-time[J].Phys Rev D,2002,66:107701.

[9] HAO J G,LI X Z.Features of motion around global monopole in asymptotically dS/AdS space-time[J].Class Quantum Grav,2003,20:1703-1714.

[10] LI X Z,LU J Z.Global monopoles in the Brans-Dicke theory[J].Phys Rev D,2000,62:107501.

[11] JIN X H,LI X Z,LIU D J.Gravitating global k-monopole[J].Class Quantum Grav,2007,24:2773-2780.

[12] LIU D J,ZHANG Y L,LI X Z.A Self-gravitating Dirac-Born-Infeld Global Monopole[J].Eur Phys J C,2009,60:495-500.

[13] BORN M,INFELD L.Foundations of the New Field Theory[J].Proc R Soc London A,1934,144:425-451.

[14] EDDINGTON A S.The Mathematical Theory of Relativity[M].Cambridge:Cambridge Unversity Press,1924.

[15] BANADOS M,FERREIRA P G.Eddington's theory of gravity and its progeny[J].Phys Rev Lett,2010,105:011101.

[16] PANI P,SOTIRIOU T P.Surface singularities in Eddington-inspired Born-Infeld gravity[J].Phys Rev Lett,2012,109:251102.

[17] SHAM Y H,LEUNG P T,LIN L M.Compact stars in Eddington-inspired Born-Infeld gravity:Anomalies associated with phase transitions[J].Phys Rev D,2013,87:061503.

[18] KIM H C.Physics at the surface of a star in Eddington-inspired Born-Infeld gravity[J].Phys Rev D,2014,89:064001.