Mass thickness measurements for dual-component samples utilizing equivalent energy of X-rays?
CHEN Min-Cong(陳敏聰) and TIAN Li-Hong(田麗鴻)
1Department of Computer and Technology,Nanjing Institute of Technology,Nanjing 211167,China
Mass thickness measurements for dual-component samples utilizing equivalent energy of X-rays?
CHEN Min-Cong(陳敏聰)1,and TIAN Li-Hong(田麗鴻)1
1Department of Computer and Technology,Nanjing Institute of Technology,Nanjing 211167,China
In this paper,equivalent energy method is introduced for measuring mass thickness of dual-component samples using dual-energy X-rays.Approximately,the method adopts equivalent mass attenuation coefficients of the two components in mass thickness measurements for dual-component samples,in a certain range of thicknesses.Feasibility of the method is proven by numerical calculations and Monte Carlo simulations(EGSnrc package).The results of absorption experiments using an X-ray machine at tube voltages of 30 and 45kV,the relative errors are less than 5%between the nominal and detected values.Also,optical low energy is discussed at given high voltages.
X-rays,Optimal dual-energy,Dual-sample,Mass thickness
I.INTRODUCTION
X-ray sources are widely used in non-destructive test,in which the beam-hardening artifact that limits the ability of X-ray quantitative analysis needs to be eliminated[1,2].In medical applications,optimal energies for dual-energy computed tomography and optimal tube voltage selection for dual-energy imaging of the chest were studied,and problems of optimal dual-energy CT in different parts of medical fields were discussed[3,4].In this paper,mass thickness measurements for dual-component samples is investigated,and dualcomponent samples of aluminum and plexiglass(PMMA, poly(methyl methacrylate))are used as phantom materials in bone density measurements.
In our previous studies,the equivalent energy method was introduced in the measurement for a single sample[5],and a log-linear rate of absorption was found for a range of material thicknesses when an extra filter was used,proved by numerical calculations and measurements.In this study,this method was applied to mass thickness measurements of dualcomponent samples(Al and PMMA),by numerical calculations and absorption experiments.
II.MATERIAL AND METHODS
A.Equivalent energy method
Electron beam-induced X-rays consist of continuous and characteristic X-rays.In the equivalent energy method,a suitable filter is used to absorb the characteristic photons and to pre-harden X-ray spectra at a special voltage.The hardened spectra have a peaked energy distribution and the beamhardening effect can be ignored for a certain range of sample thicknesses.
B.Numerical calculations
Considering the effects of photoemission,Compton scattering,Rayleigh scattering and electron pair effect(E >1.02MeV),the photon absorption in materials can be well computed.And the results of mass thickness measurements can be calculated through numerical calculations at the base of Kramer's continuous spectra formula and the detection principles.
For current-mode detection,the current signals from a dual-materials in mass thicknesses of M1and M2are proportional to photon energy and number of photons deposited in the detector.For dual-component samples,the Eq.(1)can be obtained,
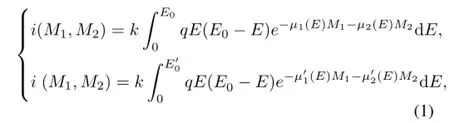
where k is the transmission factor of the detector;E0and E0are maximum photon energies that equal to the low and high voltages(VLand VH),respectively;μ1(E),μ1(E),μ2(E)and μ2(E)are mass attenuation coefficients of the two components at VLand VH,respectively;and q is the charge activated by unit photon energy.The components of kq E(E0-E)dE and kqE(E0-E)dE are the original signals before X-rays attenuation in the sample,and 100%detection efficiency is assumed.Obtaining the solutions of Eq.(1) means obtaining expressions for M1and M2as certain function of i and i .It is a complex computing process when a huge of data are treated.Using the equivalent energy method, the coefficients of μ1,μ1,μ2and μ2become constants and Eq.(1)can be written as:
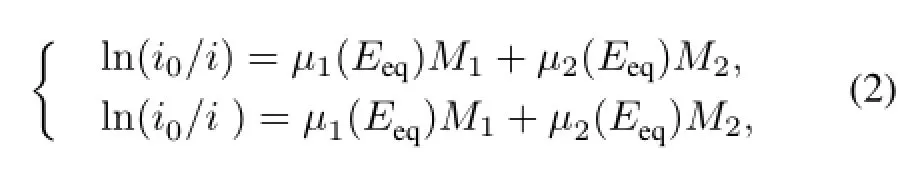
X-rays at VLand VH,respectively;i and i are the intensities of X-rays transmission at VLand VH,respectively;μ0(E) and μ0(E)are the mass attenuation coefficients of the filter at VLand VH,respectively;M0is the mass thickness of the filter;andare the equivalent mass attenuation coefficients of the two materials at the equivalent energies Eeqand,respectively.The equivalent coefficients are determined by factors of the voltages, filter material and sample thicknesses.Eq.(2)is linear in two unknown materials(M1and M2)if the other parameters are identified.This reduces computing time and increases the computation accuracy.In this paper,the dual-component samples are comprised of different pieces of 0.35-mm thick aluminum and 2-mm thick plexiglass.
C.Monte Carlo Simulation
Monte Carlo simulation using EGSnrc packages are widely used in absorption simulation[6,7].It can simulate the transport of electrons and photons in an arbitrary geometry for particles from a few keV to several hundreds of GeV in energy[8].The geometry configuration used in our simulation is shown in Fig.1.A total of 108particle tracks are simulated. The photons passing through samples are scored excluding the scattering ones.

Fig.1.Geometry configuration of the experiment.
D.Experiments
The experimental setup is shown in Fig.1.The X-ray generator with a Cu target is from Dandong High-voltage device factory,Liaoning,China.A Ni filter of 0.2mm thickness is used at low tube voltages,while 1-cm thick Cu is used at high tube voltages.Collimated X-rays pass through the dualcomponent sample of 0.35-mm aluminum and 2-mm plexiglass.The detector is of GOS scintillator and silicon photodiode.An HPGe detector with a 0.127-cm thick Al window is used,too.
E.Error analysis
In this section we will discuss the errors of the equivalent energy method at different tube voltages.From Eq.(2),M1and M2depend closely on mass attenuation coefficients of the two components.From NIST[9],both mass attenuation coefficients of aluminum and plexiglass decrease with increasing photon energy in 10–100keV,but the coefficients are insensitive to the photon energy above 100keV.So,low energy X-rays(E <100keV)relatively play an important role on the coefficients.In this paper,high energy X-rays generated with tube voltage of 140kV is preseted,and low tube voltages 50kV,60kV,70kV,80kV and 90kV are chosen to study their effects on the mass attenuation coefficients. Here,we will take the solution of M1as an example.According to Eq.(2),the solution of M1can be written as:

Suppose the detector readings at different voltages are not correlated.For a tiny change in M1,Eq.(3)can be written as:

III.RESULTS AND DISCUSSION
A.Numerical calculations and M-C simulation
Figure 2 shows ln(i0/i)as a function of mass thickness of aluminum and plexiglass,at tube voltage of 70kV using 0.2-mm Ni filter,and at 140kV using 1-cm Cu filter.The results were obtained by M-C simulation with the EGSnrc codes.The equivalent attenuation coefficients are similar in mass thickness range under investigation for the two materials,hence the feasibility of the equivalent energy method in mass thickness measurements for dual-component samples.
According to Eq.(2),μ1,μ1,μ2and μ2should be identified first to obtain the solutions of M1and M2.Approximately,the equivalent mass attenuation coefficients of the two single-components can be used.Surely,this brings extra errors in the computations as X-rays are hardened more in the dual-component samples than in the single-component sample.The errors are studied by numerical calculations,at tube voltage of 70 and 140kV,with different thickness combinations of the two components.The results are given in Table 1.The relative errors are less than 2%for two components when the X-ray energy is increased.

TABLE 1.Relative errors of mass thickness(g/cm2)between specified values and numerical calculations

TABLE 2.The detected and nominal mass thicknesses(g/cm2)of Al and PMMA samples.The nominal values are provided by the manufacture

Fig.2.Relationships between ln(i0/i)and mass thickness of aluminum(a)and plexiglass(b)obtained by EGSnrc and numerical calculations.
B.Experimental errors
The experimental results of mass thickness measurements for the dual-component samples(Al and PMMA)are given in Table 2.The two X-ray energies were 30 and 45kV.The tube current was 30mA to ensure enough intensity of X-rays. A 0.2-mm Ni filter was used.The detector output of over 10000 was ensured to reduce the background.From Table 2, the errors are less than 5%in the thickness ranges of the dualcomponent under investigation.
For quantitative description of the degree of spectrumhardening,X-ray spectra with and without a 1.4-cm thick PMMA sample were measured at 35kV using an HPGe detector(Fig.3).Peak positions of the two spectra are close to each other.So the equivalent energy of X-ray can be treated as a constant in the experiment using the HPGe detector with a 0.127-cm Al window.The results show that the equivalent energy in the experiments is near the peak position.
C.Optimal low voltage
The squared statistic counting error,1/N(N is the number of photons),as a function of low voltages is shown in Fig.4.The results were obtained by EGSnrc M-C simulation of different thickness combinations of Al and PMMA, assuming a 100%detection efficiency.The statistical errors are insensitive to the Al and PMMA thickness combinations

Fig.4.Statistical errors in different thickness combinations of two materials at different low voltages.
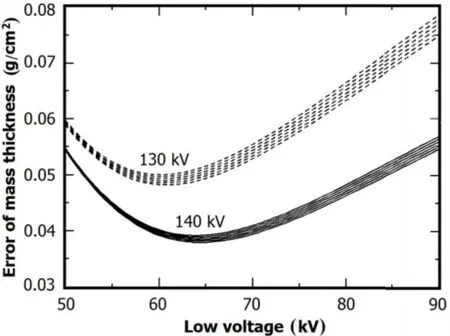
Fig.5.Errors caused by different kV combinations with different thickness compositions of two components by numerical calculations.
in the thickness range under investigation.The curves of“2Al +3PMMA”and“4Al+1PMMA”overlap in Fig.4.At low voltage of over 60kV,the statistical errors of all the Al and PMMA thickness combinations are approximately constant.
The equivalent mass attenuation coefficients of Al and PMMA at low voltages of 50–90kV are calculated,with 0.2-mm thick Ni filter.The results can be fitted by exponential functions of the low voltage(x)as(R2>0.999):

We note that this paper involves just aluminum and plexiglass dual-component samples,as we are interested in human bone density measurements.Human body can be treated as dual-component samples similar to aluminum(bone mineral)and plexiglass(water or soft issue). However,the method shall be effective in other dual-component samples of different materials,if the equivalent energy can be found. And the numerical calculations model will be helpful when the materials are known.
IV.CONLUSION
Equivalent energy method is introduced in mass thickness measurements for dual-component samples.In this method, linear equations,rather than integral equations,are solved, hence a simple and fast approach,with low demand on detectors.Based on known composition of the dual-components, it can be applied to DEXA(dual-energy X-ray absorptiometry)and Dual-energy CT in diagnostics of either a human body or a printed circuit board.With knowledge of the nature of materials,feasibility of the equivalent energy method can be predicted by numerical calculations and give guidance in the experiments.The results of Monte Carlo simulation agree well with those by numerical calculations in this paper.In the range of Al and PMMA thickness combinations under investigation,relative errors of numerical results are less than 2%. Considering the counting statistical errors,an optimal low voltage is found for a preseted high voltage.As an effective way to examine mass thicknesses of dual-component samples,the equivalent energy method can be well applied in clinics and industries.
[1]Fu J and Lu H N.Nucl Instrum Meth A,2006,556:379–385.
[2]Bisogni M G,Del Guerra A,Lanconelli N,et al.Nucl Instrum Meth A,2007,581:94–98.
[3]Talbert A J,Brooks R A,Morgenthaler D G.Phys Med Biol, 1980,25:261–269.
[4]Shkumat N A,Siewerdsen J H,Dhanantwari A C,et al.Med Phys,2007,34:3916–3925.
[5]Chen M C,Li H M,Chen Z Y,et al.Appl Radiat Isotopes,2008, 66:1387–1391.
[6]Ali E S M and Rogers D W O.Phys Med Biol,2008,53: 1527–1543.
[7]Chow J C L.Radiat Phys Chem,2010,79:567–574.
[8]http://www.irs.inms.nrc.ca/inms/irs/ EGSnrc/EGSnrc.html.
[9]http://www.physics.nist.gov/PhysRefData/ X-rayMassCoef/tab3.html.
(Received November 18,2013;accepted in revised form March 3,2014;published online July 27,2014)
10.13538/j.1001-8042/nst.25.040202
?Supported by Nanjing Institute of Technology(No.121107090001)?
,mcchen@mail.ustc.edu.cn
 Nuclear Science and Techniques2014年4期
Nuclear Science and Techniques2014年4期
- Nuclear Science and Techniques的其它文章
- Simulation studies on two-frequency RF gun
- Tidal effects on hydrostatic leveling system used in high precision alignment of particle accelerator?
- External micro-PIXE analysis of Nd3+accumulation in Euglena gracilis?
- Synthesis of N,N′-dimethyl-N,N′-didecyl-3-oxa-diglycolamide for extraction of lanthanides?
- A K-CELL injection system for SH-PermEBIT?
- Improved preparation and chemical kinetics on fully automated synthesis of[18F]-THK523,a PET imaging probe for Tau pathologies?
