The flow characteristics of fluid in micro-channels of different shapes?
WU Ge-Ping(吳鴿平),WANG Jun(王俊),and LU Ping(陸平)
1School of Energy and Power Engineering,Jiangsu University,Zhenjiang 212013,China
The flow characteristics of fluid in micro-channels of different shapes?
WU Ge-Ping(吳鴿平),1,WANG Jun(王俊),1and LU Ping(陸平)1
1School of Energy and Power Engineering,Jiangsu University,Zhenjiang 212013,China
In this paper,we study hydrodynamics and thermal behaviors of micro-heat exchanger of different cross sections,with hydraulic diameters(Dh)of 0.4–0.8mm and Reynolds numbers(Re)of 300–900.Validity of the model is proved by comparing simulation results based on classical Navier-Stokes equations with experimental data and Tuckerman correlation.Effects of dynamic viscosity,hydraulic diameter,Reynolds number and cross section of the micro-channels are investigated.The results indicate that the variable viscosity effect should be taken into account,and rod bundle micro-channels have the highest heat transfer coefficient of the three types of micro-channels.
Non-uniform heating,Variable viscosity effect,Po number,Thermal efficiency
I.INTRODUCTION
Compact heat exchangers based on micro-channels show a nice foreground over miniature nuclear power system,and learning flow behaviors of fluid in micro-channels is of importance for designing micro-fluidic systems.
Investigations[1–5]have been devoted to flow characteristics of water in micro-channels.Koo and Kleinstreuer[6] studied viscous dissipation effects on convection through circular and rectangular micro-channels and concluded that viscous heating was a function of the hydraulic diameter,the channel aspect ratio,and the Brinkman number,and that ignoring viscous dissipation could affect accurate flow simulation in micro-channels.
Judy et al.[7]experimented with distilled water,methanol, and isopropanol in round and square micro-channels fabricated from fused silica and stainless steel,and measured frictional pressure drop in hydraulic diameters of Dh=15–150μm over Reynolds number of Re=8–2300.The results showed that the values of fRe agreed well with the conventional Stokes flow theory over the tested range of Reynolds numbers.
Gamrat et al.[8]performed both two-and threedimensional numerical simulation to analyze thermal entrance effects on micro-channel convection.They found that the continuum model of conventional mass,Navier–Stokes and energy equations were adequately accurate to simulate the fluid flow and heat transfer for the micro-channels.
Against researches in the past decade in a micro-channel of single shape,however,there is just a handful of studies, experimental or theoretical,on flow characteristics of microchannels in different shapes.In this paper,we study hydrodynamic and thermal behavior of fluid flow in micro-channel heat exchanger of different shapes.The effects of dynamicviscosity,hydraulic diameter,Reynolds number and cross sections are investigated.
II.EXPERIMENTAL SETUP
The experimental system used in this study is divided into three parts–the test section,the water driving system,and the dynamic data acquisition section,as shown schematically in Fig.1.
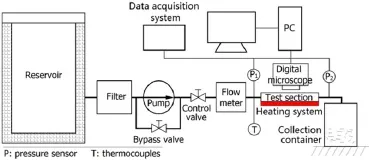
Fig.1.(Color online)Schematic of the experimental system.
Effectivehermeticallysealingandheatinsulatingmeasures weretakenforthetestsection.Fluidflowthroughthetestsection could be adjusted by the control valve.Deionized water was used as the working fluid.A flow meter was connected at the entrance of the test section.Two pressure sensors were fixed on the inlet and outlet ducts to measure pressure.Type-K thermocouples were selected to measure temperatures of solid wall and liquid.Heating pillars powered by a DC power supply,which can be regulated,were used to supply constant heat flux.The measurement signals were transmitted to a computer.
The physical configurations of the micro-channels heat exchanger are shown schematically in Fig.2.The dimensions of cooling passages are given in Table 1.
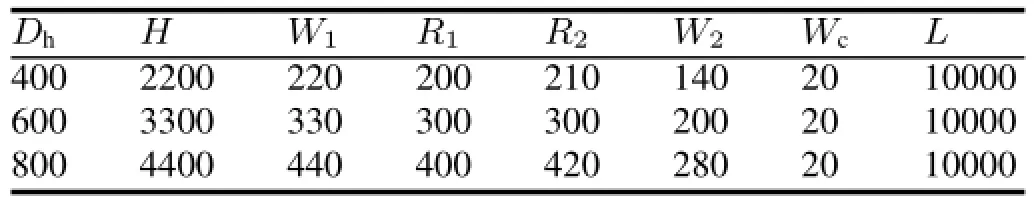
TABLE 1.Dimensions of the micro-channels(μm)
III.MATHEMATICAL MODEL
According to the literature,Navier-Stokes equations are still valid for laminar flow of water in micro-channels of hydraulic diameter as small as 0.4mm.The model is derived from continuum based on conservation equations of mass, momentumandenergy,withthefollowingbasicassumptions: (1)negligibleeffectofgravityandotherforms ofbodyforces, (2)incompressible Newtonian fluid,and(3)steady laminar flow.
The governing equations are Eqs.(1)–(3),the equations of continuity,momentum and energy,respectively.
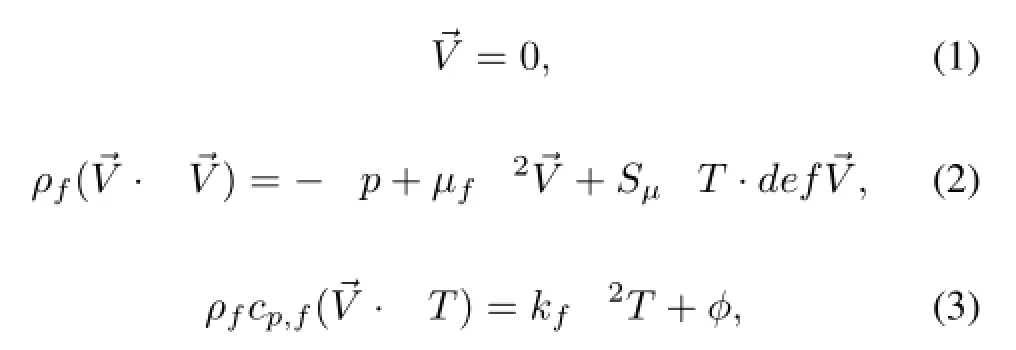
where,ρfis water density,p is pressure,→V is the velocity, kfis the water thermal conductivity,ksis the silicon thermal conductivity,μfis the viscosity of the water,cp,fis specific heat of water,T is temperature.
For the solid,Eq.(3)can be written as:

with viscosity-temperature sensitivity as:

and the viscous dissipation term as:
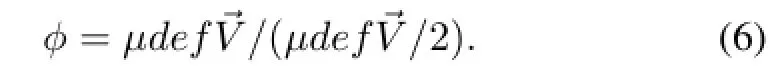
The viscosity is calculated by the parameters supplied by the NIST in the temperature range of liquid water,given as:
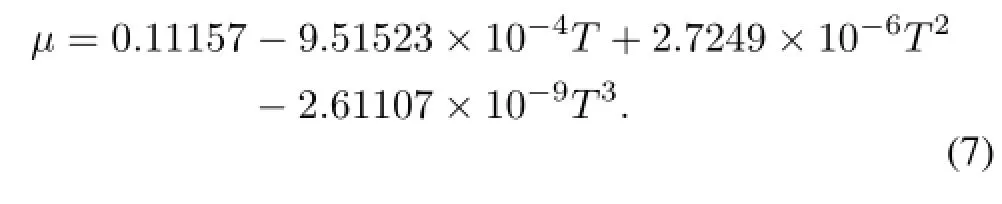
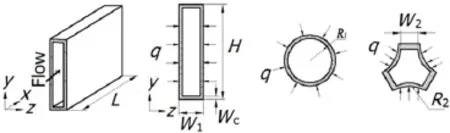
Fig.2.Schematic diagram of computational domain.
The boundary conditions at the inlet,the outlet,the heating surface and the fluid-solid interface are given by Eqs.(8)–(11),respectively.
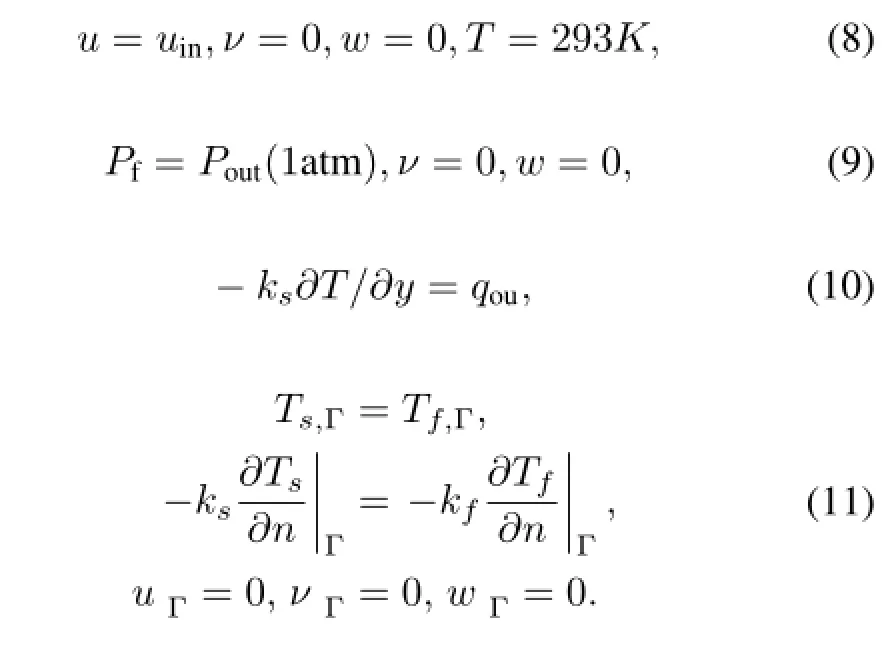
The governing equations with boundary conditions were solved by the commercial CFD code,FLUENT.The equations were discretized by means of a fully implicit second order finite volume method with modified upwind advection scheme.The SIMPLE algorithm is used to resolve the pressure-velocity coupling.The numerical solution process is shown in Fig.3.
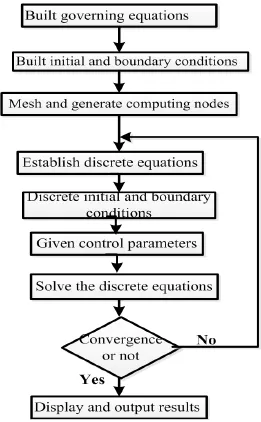
Fig.3.The solution process.
IV.EXPERIMENTAL RESULTS

Fig.4.Comparison of the experimental and simulation results for fRe(a),and heat transfer coefficient as a function of Re(b).
The experimental and simulation results for the fRe and heat transfer coefficient as a function of the Re number,are plotted in Fig.4.The trends of experimental data and predicted curve are in good agreement over the entire range of Reynolds number being studied.
To compare with experimental data,the local thermal resistance is calculated using
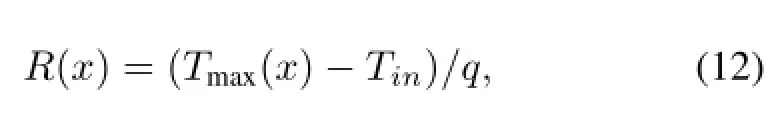
where,R(x)and Tmax(x)are thermal resistance and maximum temperature at x cm from the entrance,Tinis inlet water temperature,and q is heat flux at the heating area.
Validation of the numerical method was performed under uniform heat flux condition over the two side faces,as a benchmark case.Fig.6 shows the thermal resistance data measured in this work and results by Tuckerman[9].It can be seen that they agree well.The slight differences may be caused by different physical properties and outlet conditions.Apparently,the numerical method is appropriate for the present study.
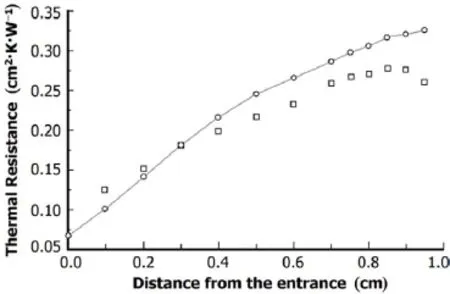
Fig.5.Comparison of the measurement results(?)of thermal resistance with the data(□)by Tuckerman[9].
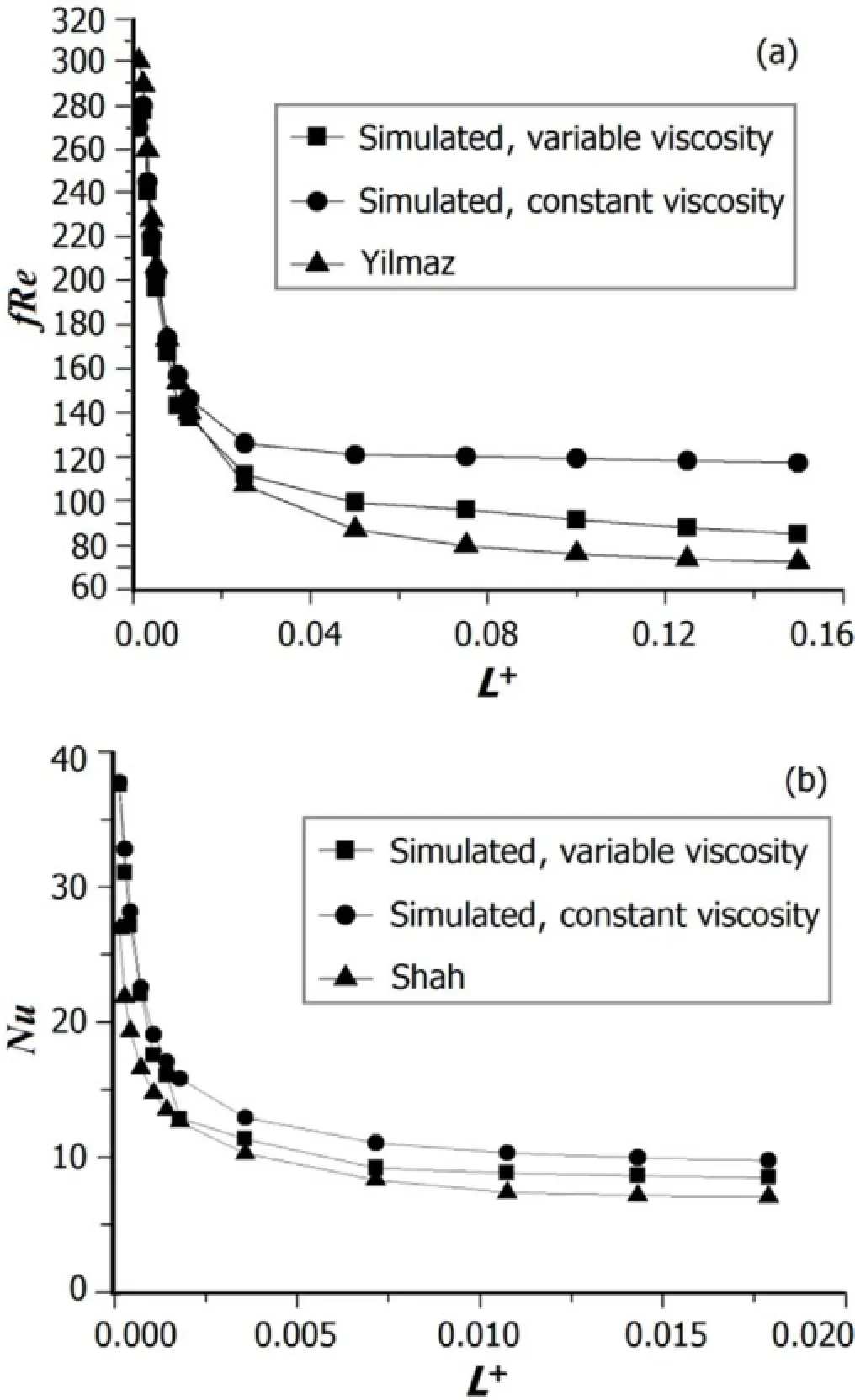
Fig.6.The local fRe(a)and local Nusselt numbers(b)as a function of L+.
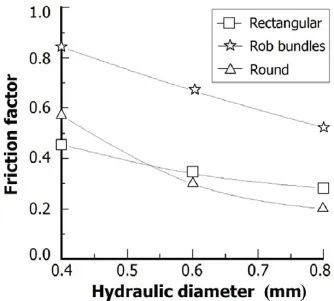
Fig.7.Friction factor vs.hydraulic diameter for micro-channel of different shapes.

Fig.8.Effects of heat flux uniformity on the fRe(a)and thermal efficiency of micro-channel of different shapes(b).
V.DISCUSSION
As shown in Fig.6(a),the local fRe we simulated is in good agreement with analytical solution by Yilmaz[10]:
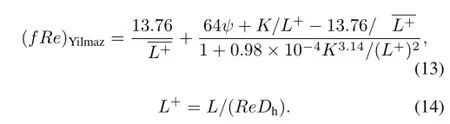
The fRe reaches a constant value of about 120 when the hydrodynamic flow develops fully with a constant viscosity. However,the viscosity varies actually due to increasing water temperatures,and the fRe decreases continuously,as shown in Fig.6(a).Therefore,the viscosity effect should be taken into account.
The calculated local Nusselt numbers agrees well with the theoretical results by Shah[11],too,as shown in Fig.6(b). The data of variable viscosity are always less than the data of constant viscosity,as the viscous dissipation decreases heat transfer efficiency.Differences in two sets of data disappear gradually with the flow development,as the viscous dissipation effects decrease.
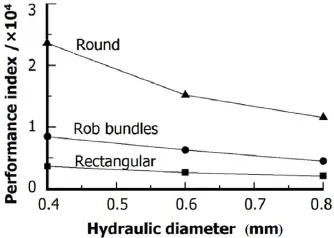
Fig.9.Thermal efficiency vs.Dhfor three types of micro-channels.

Fig.10.Nusselt number as a function of Dhunder uniform or nonuniform heating condition.
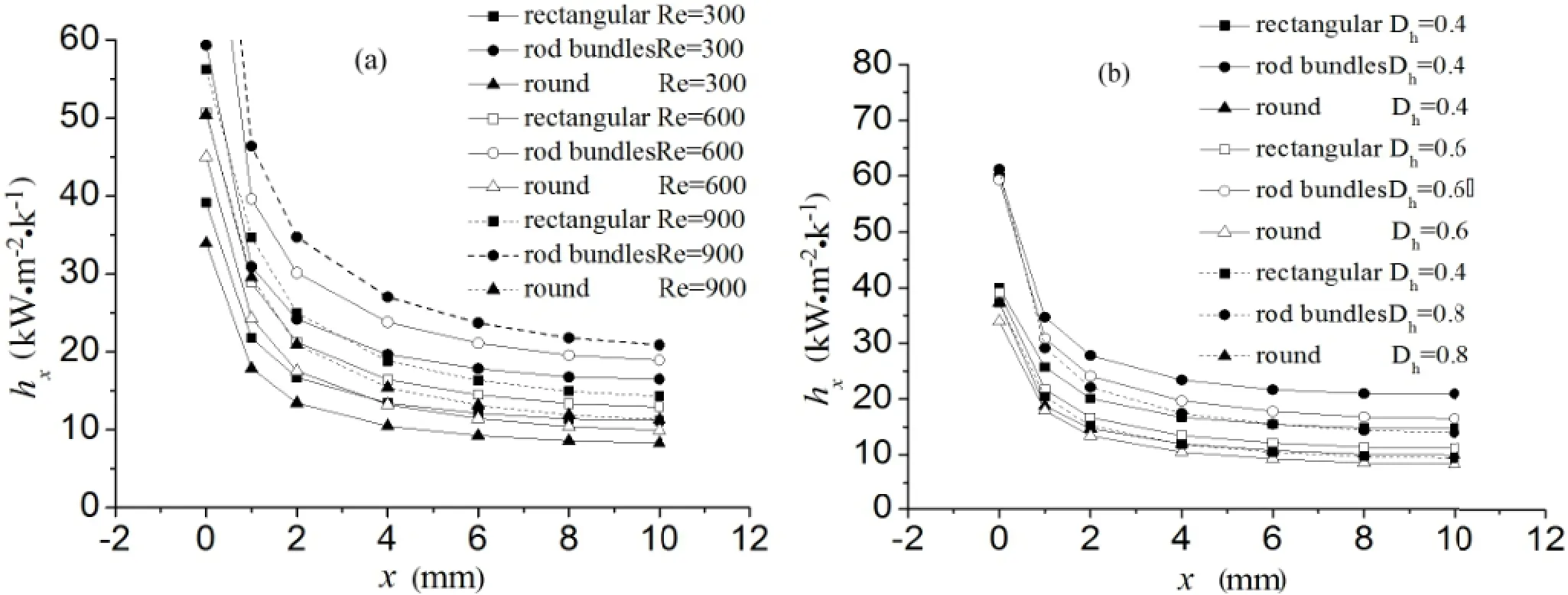
Fig.11.Effect of Reynolds number(a)and hydraulic diameter(b)on heat transfer for the three types of micro-channels.
The friction factors of laminar flows,as a function of hydraulic diameter,are shown in Fig.7 for micro-channels in rectangular,round and rob bundle cross-sections.For the same cross-section,the friction factor decreases with increasing Dh.The rob bundle micro-channels have the highest friction factor,which causes the greatest energy dissipation. On the other hand,for Dh=0.6–0.8mm,the round microchannels have the smallest friction factor.
Figure 8(a)shows that the fRe rises with Reynolds numbers under both uniform or non-uniform heat flux,but the fRe curve of non-uniform heating is always higher than that of the uniform heating,and the differences increase gradually with Re.
The performance index,defined as the ratio of heat transferred to total pumping power,is introduced for better understanding of the overall performance of the micro-channels,
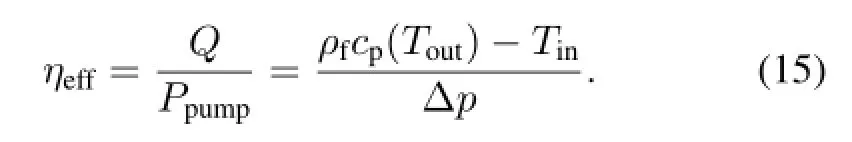
Figure 8(b)shows the performance index,as a function of theReynoldsnumber,ofdifferentlyshapedmicro-channelsof the same hydraulic diameter.Generally,the performance index decreases with increasing Reynolds number.This is due to the increased pressure drop which results in higher pumping power as the flow rate increases.
The performance index of different types of microchannels with the same Reynolds numbers is illustrated in Fig.9.The performance index decreases with increasing hydraulic diameter.Of all types of micro-channels,the round type has the highest performance index.The rod bundles type holds the second place.
Figure 10 shows the distributions of the Nusselt number (Nu)at different distances(x)from the entrance,under nonuniform or uniform heat flux at a specified Reynolds number. The Nusselt number of non-uniform flux is much higher than that of uniform heating condition at 5mm < x< 30mm due to the high heat flux in this region.The Nusselt number increases with the increase of heat flux.
As shown in Fig.11(a),the heat transfer coefficient(hx, in kWm-2K-1)increases with the Reynolds number at Dh=0.6mm for all the three types of micro-channels.The heat transfer enhancement contributes mainly to the thinner boundary layer at the higher Reynolds numbers.Fig.11(b) shows the Dheffectsonheattransfercoefficient atRe=300. The heat transfer coefficient is greater at smaller hydraulic diameters,and it decreases along the flow direction of all the three types of cooling passages,as the flow becomes regular and the boundary layer thickens.The heat transfer coefficient is the highest at entrance region of the micro-channels,due to the entrance effect.Of the three types of micro-channels, the rod bundle type has the highest heat transfer coefficient, followed by rectangular type.
VI.CONCLUSION
The Navier-Stokes equations is still valid in the present study,and the variable viscosity effect should be taken into account.For our micro-channel configurations,the fRe increases almost linearly with the Re number.The heat transfer coefficient and thermal efficiency of micro-channels of the rod bundles is superior to the other channels.
[1]Yue J,Chen G,Yuan Q,et al.Chem Eng Sci,2007,62:2096–2108.
[2]Zhao T S and Bi Q C.Heat Mass Transfer,2005,48:3637–3647.
[3]Morini G L and Spiga M.Heat Transfer Eng,2007,129:308–318.
[4]Haddad O,Abuzaid M,Al-Nimr M.Entropy,2005,6:413–426.
[5]Khadrawi A F,Othman A,Al-Nimr M.Int J Thermophys, 2005,26:905–914.
[6]KooJandKleinstreuerC.HeatMassTransfer,2004,47:3159–3169.
[7]Judy J,Maynes D,Webb B W.Heat Mass Transfer,2002,45: 3477–3489.
[8]Wu H Y and Cheng P.Heat Mass Transfer,2003,46:2519–2525.
[9]Tuckerman D B and Pease R F.Electron Devic Lett,1981,2 126–129.
[10]Yilmaz T.J Enery Resour-ASME,1990,112:220–223.
[11]Shah R K and London A L.Laminar Flow Forced Convection inDucts(AdvancesinHeatTransfer,Supplement1).NewYork (USA):Academic Press,1978.
(Received October 22,2013;accepted in revised form December 17,2013;published online July 7,2014)
10.13538/j.1001-8042/nst.25.040601
?Supported by National Natural Science Foundation of China(No. 51106067),China Postdoctoral Science Foundation(No.2012M511212) and Foundation of Priority Academic Program Development of Jiangsu Higher Education Institutions
?Corresponding author,gpwu@mail.ujs.edu.cn
 Nuclear Science and Techniques2014年4期
Nuclear Science and Techniques2014年4期
- Nuclear Science and Techniques的其它文章
- Development of a beta radioluminescence nuclear battery?
- Apparatus for determining permeability of hydrogen isotopes in molten-salt
- A facile method to build a proton nanosensor with neutral to basic pH sensitive range?
- Hadron multiplicities in p+p and p+Pb collisions at the LHC?
- An investigation on neutron induced reactions on stable CNO isotopes?
- Readout electronics for CSR-ETF silicon strip array detector system?
