樊丹, 楊晗

(1.西南交通大學(xué)希望學(xué)院, 成都 610031; 2. 西南交通大學(xué)數(shù)學(xué)學(xué)院, 成都 610031)

非齊次非對稱波動方程的Strichartz估計

樊丹1, 楊晗2

(1.西南交通大學(xué)希望學(xué)院, 成都 610031; 2. 西南交通大學(xué)數(shù)學(xué)學(xué)院, 成都 610031)

通過研究齊次非對稱波動方程的解, 應(yīng)用Duhamel’s原理, 得到非齊次非對稱波動方程柯西問題的形式解. 與此同時, 借助Hardy-Littlewood-Sobolev 與H˙o˙lder不等式, 給出這類非齊次方程解的Strichartz估計.

Strichartz估計; 非齊次非對稱波動方程;Duhamel’s原理

1 引言

本文研究非齊次非對稱波動方程解的Strichartz估計, 方程如下:

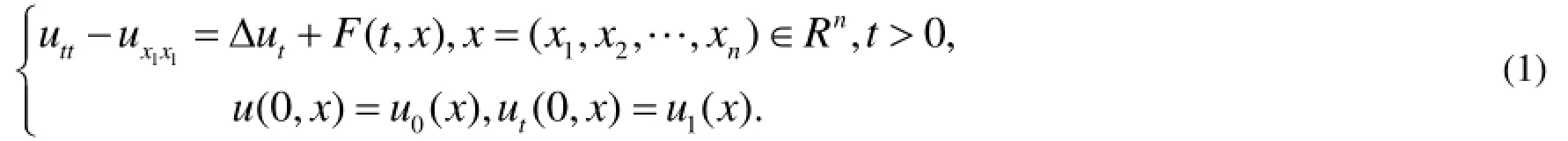
文[6]關(guān)于齊次非對稱波動方程解的Strichartz估計結(jié)果如下:

引理1.1[6](Strichartz估計) 若u(x,t)為方程(1)的解, 則對于任意的容許對(q,r)且(q,r)≠(2,∞), 這時存在CT(T＜∞), 對于任意的u0,u1∈Hn+1,1, 我們有:

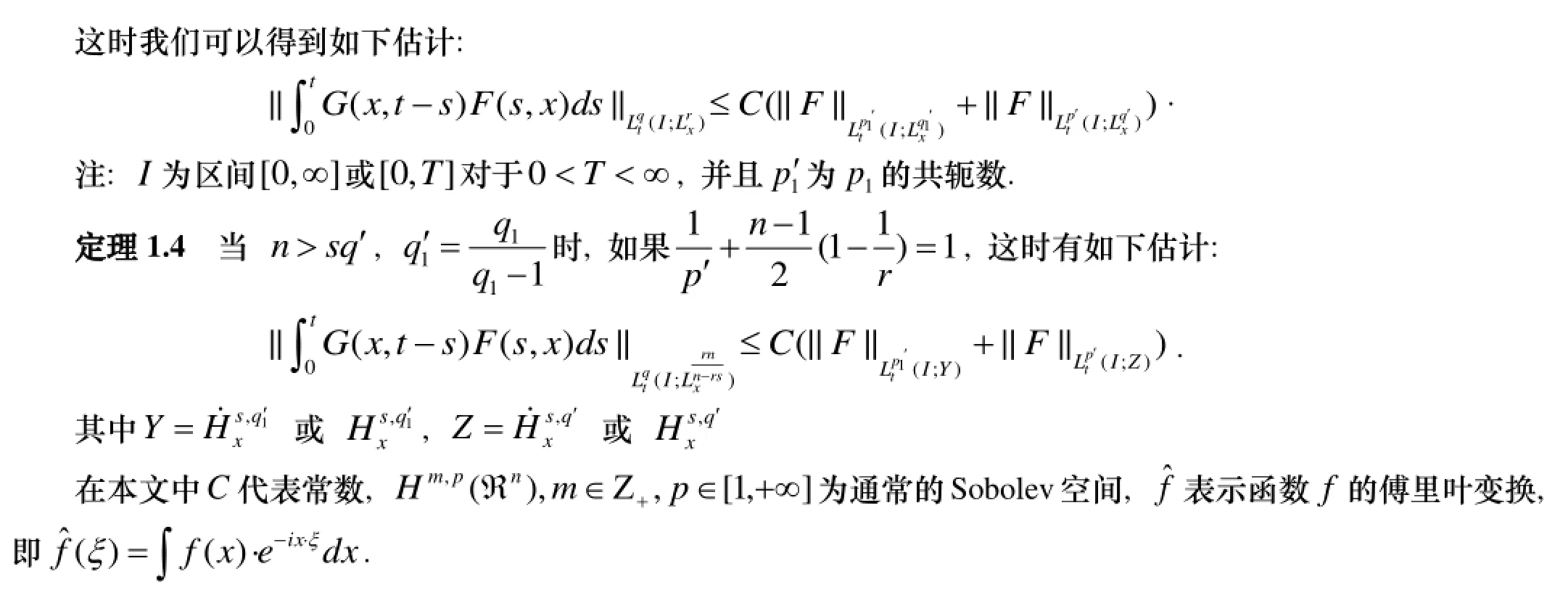
2 準(zhǔn)備工作

3 定理1.3的證明

4 定理1.4的證明

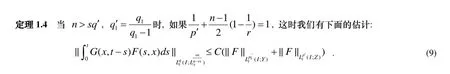
[1] KEEL M, TAO T. Endpoint Strichartz inequalities[J]. Amer J Math, 1998, 120: 955-980.

[2] J INIBRE, G VELO. Generalized Strichartz inequalities for the Wave Equation[J]. J Func Anal, 1995, 133: 50-68.

[3] J GINIBRE, G VELO. he global Cauchy problem for the critical nonlinear wave equation[J]. J Funct Anal, 1992, 110: 96-130.

[4] P BRENNER. On Lp-Lqestimates for the wave equation[J]. Math Z, 1975: 145, 251-254.

[5] 王成波. Strichartz估計與非線性波動方程的適定性問題[D]. 杭州: 浙江大學(xué)博士論文, 2007.

[6] YONGQING LIU, YI ZHOU.Lp-Lqestimates on the solutions to utt-ux1x1=Δut(2008).arXiv:0809.1147 v1[math.AP] 6, 2008.

[7] 樊丹, 楊晗. 齊次非對稱波動方程的Strichartz估計[J]. 西南民族大學(xué)學(xué)報: 自然科學(xué)版, 2010(6):939-943.

[8] ZHICHUN ZHAI. Strichartz type estimates for fractional heat equations[J]. J Math Anal Appl, 2009, 356: 642-658.

Strichartz estimates for asymmetric nonhomogeneous wave equation

DAN Fan, HAN Yang
(1. School of Mathematics,Hope College,Southwest Jiaotong University, Chengdu 610031, P.R.C.; 2. School of Mathematics, Southwest Jiaotong University, Chengdu, 610031, P. R. C.)

The solutions for inhomogeneous asymmetric wave equation are obtained, with the help of the solutions for the homogeneous asymmetric wave equation and Duhamel principle. Meanwhile, the Strichartz estimates on solutions to asymmetric nonhomogeneous wave equations are established by Hardy-Littlewood-Sobolev andH?lder inequality.

Strichartz estimate; asymmetric nonhomogenous wave equation;Duhamel’sprinciple

O175

A

1003-4271(2014)01-0087-04

10.3969/j.issn.1003-4271.2014.01.18

2013-11-27

樊丹(1985-), 女, 山西運城人, 助教, 碩士; 楊晗(1969-), 男, 重慶潼南人, 教授, 博士, 研究方向:非線性發(fā)展方程研究.