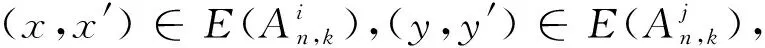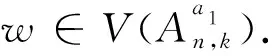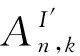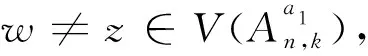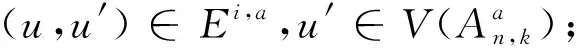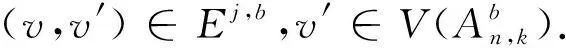排列圖的若干k*-連通性
徐 輝
(浙江師范大學(xué) 數(shù)理與信息工程學(xué)院,浙江 金華321004)
1 引言及預(yù)備知識
我們通常用一個連通的無向圖G=(V;E)表示互聯(lián)網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu),圖G的頂點代表網(wǎng)絡(luò)中的組件,圖G的連線代表網(wǎng)絡(luò)中組件之間的通信聯(lián)系[1].星圖是一個廣泛研究的網(wǎng)絡(luò)結(jié)構(gòu),而排列圖是星圖的一類分支,但它的階卻比星圖更具有靈活性.排列圖是點可遷圖也是邊可遷圖,而且當(dāng)n≥3,k=n-1時,它同構(gòu)于星圖;當(dāng)n≥2,k=1時,它同構(gòu)于完全圖.
首先令n,k為兩個整數(shù),且1≤k
V={p=p1p2…pk|pi∈ 邊集 E={(p,q)|?唯一的i,使得pi≠qi,1 ≤i≤k}. An,k為k(n-k)-正則圖.若p∈V,p=p1p2…pk,定義 EXT(p)= 稱之為p的外元素,|EXT (p)|=n-k.[2] 若u,v是一個圖G中的兩個不同的點,且u,v存在圖G中的k條內(nèi)不交的路,則稱這k條路為u,v間的k條容器,并記為k-(u,v)容器.若k-(u,v)容器的所有路中包含圖G中所有的頂點,則稱k-(u,v)容器為k*-(u,v)容器.?u,v∈V(G),u與v間都存在k*-(u,v)容器,則稱圖G為k*-連通的.一個圖G是k*-連通的,且1 ≤k≤κ(G),則稱圖G為超支撐連通圖,其中κ(G)為圖G的點連通度.根據(jù)上面定義,若一個圖中的任何兩點間都存在哈密頓路,則這個圖為哈密頓連通圖,即等同于1*-連通圖;若一個圖含有一個哈密頓圈,則這個圖是哈密頓圖,即2*-連通圖. K Day和A Tripathi證明了當(dāng)n≥2,n-k≥2時,排列圖是哈密頓連通圖[3],即排列圖是1*-連通圖.而且他們也證明了當(dāng)n≥3,n-k≥1時,排列圖是哈密頓圖[4],即排列圖是2*-連通圖. 若(u,v),(u′,v′)是Ei,j中兩條不同的邊,{u,v}∩{u′,v′}=?,則 性質(zhì)2[5]k≥2,n-k≥2時,若u,v是An,k中的兩個不同點,且d(u,v)=1,則|EXT (v)|=n-k-1,當(dāng)k=1時,An,1?Kn,Kn為完全圖. 引理1[6]當(dāng)n≥2時,An,1為超支撐連通圖. 引理2[5]假定: (ⅰ)n≥4,n-k≥2,t是一個整數(shù),且1 ≤t≤k; (ⅱ)I? 定理1 當(dāng)n≥5,n-k≥3時,An,k為3*-連通圖. 證明當(dāng)k≥2,n-k≥2時,An,k為哈密頓連通圖,即?u,v∈V(An,k),u,v間存在一條哈密頓路.同樣,An,k也為一個哈密頓圖,即圖中存在一個哈密頓圈.證明An,k為3*-連通圖,只要證明?u,v∈V(An,k),An,k內(nèi)存在3*-(u,v)容器.下面用分類討論的方法來證明.主要分為兩種情形:第一種情況是u,v屬于同一個子圖;第二種情況是u,v屬于不同的子圖. T1={u,P,v}, T2={u,Q,v}, T1,T2構(gòu)成兩條內(nèi)不交的(u,v)-路. T3={u,u′,HP,v′,v}. 則T1,T2,T3構(gòu)成u,v間的3*-(u,v)容器. u=u1u2…uk-1i, v=v1v2…vk-1j. 下面來構(gòu)造u,v間的內(nèi)不交的路. T1={u,P1,x,y,Q1,v}, T2={u,P2,x′,y′,Q2,v}. T3={u,u′,HP,v′,v}. 則T1,T2,T3構(gòu)成u,v間的3*-(u,v)容器. 根據(jù)情形1和情形2就證明了定理1. 定理2 當(dāng)n≥6,n-k≥3,An,k為4*-連通圖. 證明類似于定理1的證明方法,An,k為4*-連通圖,只要證明?u,v∈V(An,k),An,k內(nèi)存在4*-(u,v)容器.下面用分類討論的方法來證明.主要分為兩種情形:第一種情況是u,v屬于同一個子圖;第二種情況是u,v屬于不同的子圖. T1={u,P,v}, T2={u,Q,v}, T1,T2構(gòu)成兩條內(nèi)不交的(u,v)-路. T3={u,w,HP1,z,v}. T3={u,w,HP1,z,v}. T4={u,u′,HP,v′,v}. 則T1,T2,T3,T4構(gòu)成了4*-(u,v)容器. u=u1u2…uk-1i, v=v1v2…vk-1j. 下面來構(gòu)造u,v間的內(nèi)不交的路. T1={u,P1,x,y,Q1,v}, T2={u,P2,x′,y′,Q2,v}. T3={u,w,HP1,z,v}. T3={u,w,HP1,z,v}. T4={u,u′,HP,v′,v}. 則T1,T2,T3,T4構(gòu)成了4*-(u,v)容器. 通過情形1和情形2就證明了排列圖是4*-連通圖. 參考文獻: [1] 徐俊明.組合網(wǎng)絡(luò)理論[M].北京:科學(xué)出版社,2007:100-102. [2]DayK,TripathiA.Arrangementgraphs:aclassofgeneralizedstargraphs[J].InformationProcessingLetters,1992,42(5):235-241. [3]DayK,TripathiA.CharacterizationofNodeDisjointPathsinArrangementGraphs[D].TechnicalReportTR91-43,ComputerScienceDepartment,UniversityofMinnesota,1991. [4]DayK,TripathiA.Embeddingofcyclesinarrangementgraphs[J].IEEETransactionsonComputers,1993,42(8):1002-1006. [5]DayK,TripathiA.Embeddingofcyclesinarrangementgraphs[J].IEEETransactionsonComputers,1993,42(8):1002-1006. [6]HsuH-Chun.TheSpanningConnectivityofthe(n,k)-StarGraphs[J].InternationalJournalofFoundationsofComputerScience2006,17(2):415-434.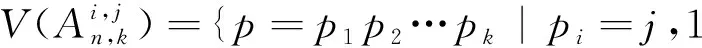
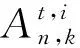
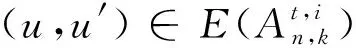
2 定理1的證明
2.1 情形1
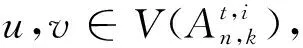
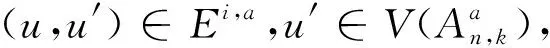
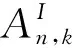
2.2 情形2
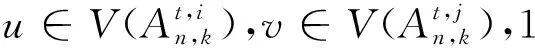
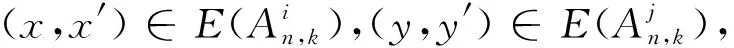
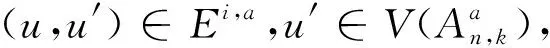
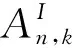
3 定理2的證明
3.1 情形1
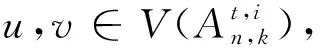
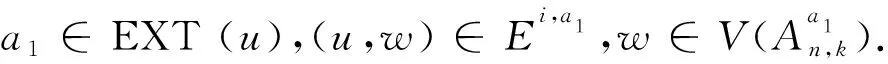
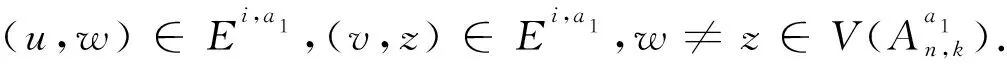
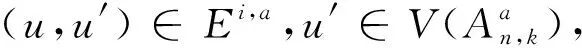
3.2 情形2