The characteristics of secondary flows in compound channels with vegetated floodplains*
LIU Chao (劉超),
State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065, China, E-mail:liuchaoscu@vip.qq.com
SHAN Yu-qi (單鈺淇)
College of Mathematics, Sichuan University, Chengdu 610065, China
YANG Ke-jun (楊克君), LIU Xing-nian (劉興年)
State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065, China
The characteristics of secondary flows in compound channels with vegetated floodplains*
LIU Chao (劉超),
State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065, China, E-mail:liuchaoscu@vip.qq.com
SHAN Yu-qi (單鈺淇)
College of Mathematics, Sichuan University, Chengdu 610065, China
YANG Ke-jun (楊克君), LIU Xing-nian (劉興年)
State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065, China
(Received February 19, 2013, Revised March 15, 2013)
The experiments were conducted in compound channels with vegetated floodplains for investigating the influence of vegetation types on the characteristics of secondary flows. In terms of the streamwise and transverse velocities and the depth-averaged velocity, the secondary flow coefficient,M, is proposed, with good physical meanings, and it may characterize the rotational direction and the intensity of the secondary currents. The experimental results show that, for the cases without vegetation and with grass, the rotational directions of the secondary flows are all anticlockwise while for the cases with shrubs, they are all changed to the clockwise direction in the whole cross-section. However, when trees are planted, the secondary flows rotate in the anticlockwise direction in the main channel and in the clockwise direction on the floodplain. In addition, for all cases, the intensities of the secondary currents on the floodplain are stronger than those in the main channel.
vegetation, secondary flows, compound channels, overbank flows
Introduction
The vegetation plays a vital role for the river corridor development which provides habitats for animals and flora, and various types of vegetations are usually found along the banks and on the floodplains of natural rivers, which alleviate the bank erosion and the soil loss. During a flood in the rain season, the flow height increases rapidly and then goes over the bank in the whole channel. The vegetation might affect the flow characteristics significantly, especially for the lateral distribution of the secondary flows closely related with the bed erosion and the sediment accumulation for the flood engineering and river engineering projects. The studies of the effects of vegetation on the flows mainly focus on trees, simulated as rigid rods or sticks, because they are easy to be analyzed and expressed by the drag force equation due to their rigidity properties with a very small deformation, as comparing with other flexible vegetation. Nevertheless, in the natural world, trees are only one typical kind of vegetation while shrubs and grass are also often seen along the bank. The characteristics of shrubs and grass are very much different from those of trees because they are flexible with leaves which will swing with the secondary flows and be easily compressed, hence, the conventional drag and projection coefficients can not describe them adequately. Their effects on the overbank flow are as important as those of trees in acompound channel, but very few related studies can be found. Therefore, the effects of vegetations, including trees, shrubs and grass, on the flow should be studied, in the context of the lateral distributions of secondary flows.

Fig.1 Different types of floodplain model vegetation
The secondary flows affect the primary mean flow and the bed shear stress distributions as well as produce a three-dimensional flow structure. Hence, a big geographic change of the mobile bedform would appear at the cross-section with strong secondary flows. In a rectangular compound channel with oneline trees on the floodplain, the distributions of the secondary currents in the whole cross-section were investigated by Sanjou et al.[1,2], and it is discovered that the vegetations affect the rotational directions of secondary flows greatly. White and Nepf[3]and James et al.[4]discovered that large-scale coherent vortices were formed between the non-vegetated and vegetated domains, and the momentum exchange which enhanced the intensities of the secondary flows was increased rapidly at the vegetation edge. Shiono et al.[5,6]experimentally investigated the characteristics of the secondary current cells for overbank flows in a meandering compound channel. The rotational directions of the secondary flows at different cross-sections were different, according to the flow height, the discharge, the bed roughness and the types of floodplain vegetations. Their studies show that the floodplain vegetations contribute to the rise of the flow height, with more energy losses between the main channel and the floodplain, accompanied with strong secondary flows, especially in cases of artificial grass on the floodplain.
Apart from the experimental studies, several analytical models were also developed to study the influences of the secondary flows. In analytical prediction models, proposed by Yang et al.[7], Hu et al.[8], Yang et al.[9], Tang and Knight[10]and Rameshwaran and Shiono[11], the governing equations include the effect of the secondary flows and it is shown that large calculation errors may be resulted by ignoring this effect. Knight et al.[12]found that the predictions of the depth-averaged velocity and the bed shear stress were more accurate in the single trapezoid channels without vegetation, the whole area should be divided into more panels because of the complex distribution of the secondary flows. This idea was further pursued by Tang et al.[13]in vegetated cases by considering the effects of secondary currents in each divided domain. In addition, another model proposed by Ervine et al.[14]also contains the influence of secondary flows by a new defined coefficient, and the models were modi- fied, considering its effect not only in the main cha- nnel but also on the floodplain, by Huai et al.[15]and Liu et al.[16]for meandering compound channels with trees on the floodplain. From the overviews of the early researches, it might be seen that the secondary flows must be considered in the analytical calculations because they affect a large number of hydraulic para- meters, such as the three-dimensional mean velocities, the flow height and the friction factor. In vegetated cases, the secondary flows in the whole cross-section can be enhanced through a stronger momentum excha- nge, and the apparent shear stress would also streng- then the interactions significantly between the vegeta- ted floodplain and the main channel[11].

Fig.2 Cross section of an asymmetric compound channel

Table 1 Summary of experimental conditions
However, the influence of vegetation types on the characteristics of the secondary flows has received relatively little attention. This paper aims to investigate the characteristics of the secondary flows in compound channels with different types of vegetation. Firstly, the experiment arrangements for compound channels with different types of vegetation, such as trees, shrubs and grass, are described. Then, the secondary flow mechanism is analyzed and the secondary flow coefficient to characterize the rotational direction and the intensity of the secondary flows is proposed. Finally, based on the experimental data, the influence of vegetation types on the characteristics of secondary flows is analyzed.
1. Experimental arrangements
A series of experiments were conducted in a flume of 16 m long, 0.3 m wide and 0.4 m high, at the State Key Hydraulics Laboratory (SKHL) of Sichuan University. The flow in the flume was in a quasi-uniform flow condition, especially in the vegetated cases, and the flow discharge and the three-dimensional velocities were measured. The flow depths were measured by means of pointer gauges while the discharges were measured by a triangular weir installed in front of the channel, and the three-dimensional velocities were measured by the Acoustic Doppler Velocimeter (ADV).
For different types of vegetation, the plastic grass, the duck feathers, and the plastic straws were selected to model the grass, the shrubs and the trees, respectively, as shown in Fig.1. The model vegetation was planted on the floodplain over a length of 3 m between 8.2 m and 11.2 m from the beginning of the compound channel, and it was planted in an interlaced way, i.e., the vegetation of the second row planted at the centerline of the first row space. The row spacing for each type of vegetation was the same, 0.03 m between individual rows, while the plant spacing took various values, i.e., 0.02 m, 0.04 m and 0.03 m for trees, shrubs and grass, respectively.
The measurement cross-section was located at 9.6 m from the inlet of the flume and ten verticals were arranged with lateral distances y from the left (y=0)to the right, 0.04 m, 0.06 m, 0.08 m, 0.11 m, 0.14 m, 0.17 m, 0.195 m, 0.22 m, 0.245 m and 0.265 m, as shown in Fig.2. For each case, three discharges, i.e., 10.95 l/s, 14.11 l/s and 17.72 l/s were considered, and the same bed slope was set, i.e., 0.125%. The measurement intervals between two vertical points were 0.0025 m, 0.004 m and 0.005 m for different flow heights. However, when the vertical distance from the measurement point to the channel bed was less than 0.005 m, the measurement interval was reduced to 0.001 m, in order to capture small changes of three dimensional velocities.
The shape of this compound channel was built as an asymmetrical one. The widths of the main channel and the floodplain were 0.08 m and 0.13 m, respectively, and the main channel side slope,s, was 1.5. The bankfull height,h, was 0.06 m and the bed surface was smoothed and covered by a thin layer of concrete. A summary of experimental conditions is given in Table 1.
2. Analysis of the secondary flow mechanism
The characteristics of secondary flows are hard to capture because they are easily disturbed and changed under different flow conditions. Therefore, a coefficient to describe the rotational direction and the inten-sity of the secondary flows is advisable. As is known, the streamwise velocity(U)and the transverse velocity (V)always change along the vertical direction, and the maximum value ofU often appears below the free surface because of the dip phenomenon due to the influence of the secondary currents[9]. Since the secondary flow may be represented by the product of U andV , therefore, one assumes thatU andV could be expressed, in terms of the depth-averaged velocity (Ud), by
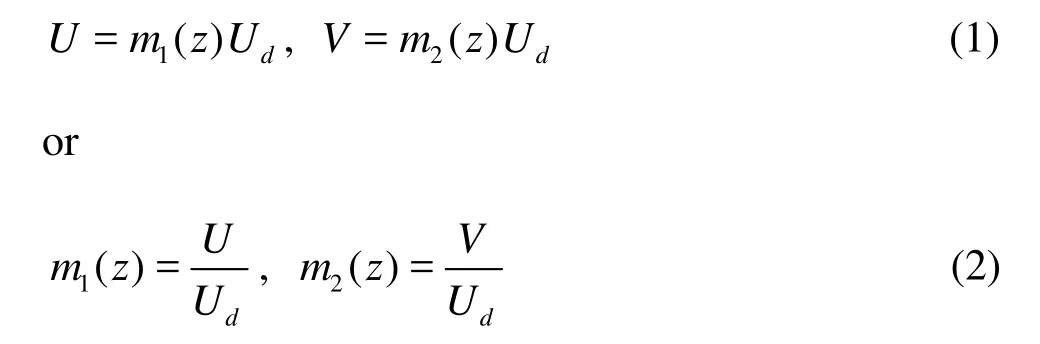


By integrating Eq.(3) from zero to the flow depth (H), the depth-averaged UV can be obtained as follows

The vertical distribution of m1( z) m2( z )is shown in Fig.4, indicating that the values of m1( z) m2( z )change from the channel bed to the surface as almost in the same manner as m2(z ), and we can observe from the experimental data that the intensity of t he s eco ndary flo w in Fig.4(b) is much strongerthanthatinFig.4(a).Alsothe absolute value of M(-0.016)in the main channel is smaller than that (0.0229) on the floodplain with trees. Hence, the intensities can be represented by the absolute M-value. From the figure, theM -value is positive on the floodplain, representing the secondary flow rotates in the clockwise direction, while it is negative in the main channel, indicating the rotational direction of the secondary current cell is anticlockwise. Therefore, theM -value itself has special physical meanings with its sign and absolute value representing the rotational direction and the intensity of the secondary flows, respectively.

Fig.3 The vertical distributions of m1( z )and m2( z )in the vegetated case (Run06)

Fig.4 The vertical distribution of m1( z) m 2( z)in the vegetated case (Run06)

Fig.5 The schematic diagram of secondary flows in compound channels with trees on the floodplain, based on the experimental data of Run06
According to the experimental data (Run06), the schematic diagram of the secondary flow is shown in Fig.5. There is one secondary flows in the main channel and on the floodplain, respectively. However, in the side sloping domain, two secondary current cells are used to simplify the complex distribution. The Udand M distributions are also shown in Fig.5. The Ud-values in the main channel are much larger than those on the floodplain and the maximum value of the Udgradient appears in the side slope region, as indicated by Tang and Knight[10]. The sign ofM is different, which keeps negative in the main channel and positive on the floodplain, and its absolute value on the floodplain is larger than that in the main channel.
3. Effects of vegetation on the characteristics of secondary flows
The secondary flow coefficient,M, is used to show the characteristics of the secondary flows for the non-vegetated and vegetated cases, i.e., with no vegetation, with trees, with shrubs and with grass on the floodplain, by using the experimental data. The characteristics of the secondary flows will be analyzed byM-values in what follows.

Fig.6 Lateral variation of secondary flow coefficient Mfor three cases without vegetation

Fig.7 Lateral variation of secondary flow coefficient Mfor three cases with emerged and submerged trees on the floodplain
3.1 The secondary flows in compound channels without vegetation
Firstly, the distribution of M in the y-direction in the cases without vegetation on the floodplain is shown in Fig.6. It is shown that the M-values all keep negative in the whole cross-section, indicating that the secondary flows rotate in the anticlockwise direction. The intensities of the secondary flows increase with the increase of the flow depth, which means that the three-dimensional velocities are increased, leading to stronger secondary current cells. The same conclusion wasreachedby Tang and Knight[10], showingthatthe intensity ofthe secondary flow increases with the rising flow height in trapezoidal channels. A stably increasing trend of the M-values was observed from the main channel to the floodplain, indicating that the intensities of thesecondary flows on the floodplain are slightly stronger than those in the main channel.
3.2 The secondary flows in compound channels with trees
TheM -values of three cases (Run04, Run05 and Run06) with trees on the floodplain are shown in Fig.7. From the figure, whether in the emerged case (Run04) or the submerged cases (Run05 and Run06), theM -values keep negative in the main channel while they keep positive on the floodplain, indicating that the rotational directions of the secondary flows are anticlockwise and clockwise in the main channel and on the floodplain, respectively. When the trees on the floodplain are emerged (Run04), the intensities of the secondary flows are much stronger than those in the submerged cases (Run05 and Run06). In three cases, the secondary currents rotate more strongly on the floodplain because the absoluteM -values are greater than those in the main channel. That may be explained by the rigid trees on the floodplain, which can be regarded as obstacles to the flow. When the trees are emerged, the flow on the vegetated floodplain has to bypass these trees and the transverse velocity increases, so the intensities of the secondary flows rise. When the trees are submerged, the water prefers to flow above the trees because of the less resistance there, leading to less loss of momentum.

Fig.8 Lateral variation of secondary flow coefficient Mfor three cases with emerged and submerged shrubs on the floodplain
3.3 The secondary flows in compound channels with shrubs
Figure 8 shows the distribution ofM -values in the whole cross-section with shrubs being planted on the floodplain. Unexpectedly, the sign of Mall changes to positive which is totally different with those in the cases with trees, as discussed before, indicating that the secondary flows rotate in the clockwise direction. When the shrubs are emerged (H=0.136 m), the intensities of the secondary currents on the floodplain are the highest among the three cases (Run08, Run09 and Run10), and the intensities of the secondary flows decrease with the increase of the flow height, especially around the centerline area. In the main channel, when the flow depth increases to submerge the shrubs (H=0.172 m, Run09), their intensities in they-direction increase rapidly, reaching nearly three times as that in the emerged case (Run08). While the submerged height of shrubs continues to increase and the flow height reachesH=0.2 m, the intensities of Run10 are only half as that of Run08.
The reasons can be attributed to the special structure of the shrub which has a large number of leaves. When the shrubs are emerged, their leaves occupy a vast space (see Fig.1(c)), as comparing with the cases with trees (see Fig.1(a)). Therefore, the water has less space to flow across the shrubs region, and the water flows round the shrubs, leading to the strengthened secondary flows. When the shrubs are submerged, the flow causes the leaves fully shaking from the beginning to the end and the rotational direction of the secondary flows is totally changed in the whole crosssection. On the floodplain, the intensity decreases following the increase of the flow height because the water has more space above the shrubs to go downstream. In addition, more momentum exchange takes place between the main channel and the vegetated floodplain due to the rising depth of the flow, hence, the intensity of the secondary flow increases with the increasing flow height in the main channel, reaching the largest at a certain submerged flow height before decreasing.

Fig.9 Lateral variation of secondary flow coefficient Mfor three cases with submerged grass on the floodplain
3.4 The secondary flows in compound channels with grass
The Mdistributions in the three cases (Run12, Run13 and Run14) with grass on the floodplain are shown in Fig.9. In the whole cross-section, nearly all values of Mare small, and it should be noted that theM -values in the three cases are almost the same, M-values are negative, which means that the secondary flows still rotate in the anticlockwise direction with the grass being planted. From the figure, it is shown that, in the main channel, the intensities of the secondary current cells are weak because the absoluteindicating that the grass affects the secondary flows slightly there. However, their intensities on the floodplain are relatively great, especially in the case with a low flow depth (Run12), and this phenomenon may be explained by the height of the grass. In the Run12, the flow height is only 0.076 m on the floodplain and the grass height ranges from 0.065 m to 0.070 m, indicating that most of the space is occupied by the flexible grass. Therefore, in the low flow level, the shaking grass strengthens the secondary flows on the floodplain. As the flow height increases, the influence of the grass seems being dwindled because the grass is compressed by the water above it and more space is provided for the flow to go downstream.
4. Conclusions
(1) A series of experiments were conducted in an asymmetrical compound channel with different vegetation types, i.e., trees, shrubs and grass, and the threedimensional velocities were measured by ADV in three different flow heights, to study the influences of vegetation on the secondary flows.
(2) In terms of the streamwise velocity(U), the transverse velocity (V)and the depth-averaged velocity(Ud), the secondary flow coefficient,M, is proposed, with good physical meanings, the sign and the absolute value representing the rotational direction and the intensity of the secondary flows, respectively. Based on the experimental data of a vegetated case (Run06), the schematic diagram of the secondary currents is shown in Fig.5.
(3) The characteristics of the secondary flows were compared by using these experimental data. In the non-vegetated cases, the secondary flows rotate in the anticlockwise direction in the whole cross-section and their intensities increase with the rising flow depth. With the trees being planted, the rotational directions of the secondary flows are changed to the clockwise direction on the floodplain and their intensities decrease with the increasing flow height. In the shrubs cases, the rotation direction of the secondary current cells is changed unexpectedly, which keeps in the clockwise direction in the whole cross-section, and the intensities go up rapidly with the rising depth of the flow in the main channel before decreasing at a certain flow height. The grass could not affect the direction of the secondary flows which still rotates in the anticlockwise direction through the whole crosssection. In the low flow height, the intensities of the secondary flows on the floodplain are very strong while they decrease rapidly with the increasing flow height, however, those in the main channel are almost the same and keep weak.
[1] SANJOU M., NEZU I. and SUZUKI S. et al. Turbulence structure of compound open-channel with one-line emergent vegetation[J]. Journal of Hydrodynamics, 2010, 22(5Suppl.): 577-581.
[2] SANJOU M., NEZU I. Large eddy simulation of compound open-channel flows with emergent vegetation near the floodplain edge[J]. Journal of Hydrodyna- mics, 2010, 22(5Suppl.): 582-586.
[3] WHITE B. L., NEPF H. D. Shear instability and coherent structures in shallow flow adjacent to a porous layer[J]. Journal of Fluid Mechanics, 2007, 593: 1-32.
[4] JAMES C. S., BIRKHEAD A. L. and JORDANOVA A. A. et al. Flow resistance of emergent vegetation[J]. Journal of Hydraulic Research, 2004, 42(4): 390-398.
[5] SHIONO K., CHAN T. L. and SPOONER J. et al. The effect of floodplain roughness on flow structures, bedforms and sediment transport rates in meandering channels with overbank flows: Part I[J]. Journal of Hydraulic Research, 2009, 47(1): 5-19.
[6] SHIONO K., CHAN T. L. and SPOONER J. et al. The effect of floodplain roughness on flow structures, bedforms and sediment transport rates in meandering channels with overbank flows: Part II[J]. Journal of Hydraulic Research, 2009, 47(1): 20-28.
[7] YANG K., NIE R. and LIU X. et al. Modeling depthaveraged velocity and boundary shear stress in rectangular compound channels with secondary flows[J]. Journal of Hydraulic Engineering, 2013, 139(1): 76- 83.
[8] HU C., JI Z. and GUO Q. Flow movement and sediment transport in compound channels[J]. Journal of Hydraulic Research, 2010, 48(1): 23-32.
[9] YANG S. Q., YU J. X. and WANG Y. Z. Estimation of diffusion coefficients, lateral shear stress, and velocity in open channels with complex geometry[J]. Water Re- sources Research, 2004, 40(5): W05202.
[10] TANG X., KNIGHT D. W. Analytical models for velocity distributions in open channel flows[J]. Journal of Hydraulic Research, 2009, 47(4): 418-428.
[11] RAMESHWARAN P., SHIONO K. Quasi two-dimensional model for straight overbank flows through emergent vegetation on floodplains[J]. Journal of Hydrau- lic Research, 2007, 45(3): 302-315.
[12] KNIGHT D. W., OMRAN M. and Tang X. Modeling depth-averaged velocity and boundary shear in trapezoidal channels with secondary flows[J]. Journal of Hydraulic Engineering, ASCE, 2007, 133(1): 39-47.
[13] TANG X., KNIGHT D. W. and STERLING M. Analytical model of streamwise velocity in vegetated channels[J]. Engineering and Computational Mechanics, 2011, 164(2): 91-102.
[14] ERVINE D. A., BABAEYAN-KOOPAEI K. and SELLIN R. H. J. et al. Two-dimensional solution for straight and meandering overbank flows[J]. Journal of Hydraulic Engineering, ASCE, 2000, 126(9): 653- 669.
[15] HUAI Wei-xin, GAO Min and ZENG Yu-hong et al. Two-dimensional analytical solution for compound channel flows with vegetated floodplains[J]. Applied Mathematics and Mechanics (English Edition), 2009, 30(9): 1121-1130.
[16] LIU Chao, YANGKe-junandLIUXing-nianetal.Analytical models for overbank flows in meandering channels with vegetated floodplains[J]. Journal of Sichuan University (Engineering Science Edition), 2012, 44(6): 7-12(in Chinese).
[17] HUAI W. X., ZENG Y. H. and XU. Z. G. et al. Threelayer model for vertical velocity distribution in open channel flow with submerged rigid vegetation[J]. Adva- nces in Water Resources, 2009, 32(4): 487-492.
[18] HUAI Wen-xin, CHEN Zheng-bing and HAN Jie et al. Mathematical model for the flow with submerged and emerged rigid vegetation[J]. Journal of Hydrodynamics, 2009, 21(5): 722-729.
[19] HUTHOFF F., AUGUSTIJN D. C. M. and HULSCHER S. J. M. H. Analytical solution of the depth-averaged flow velocity in case of submerged rigid cylindrical vegetation[J]. Water Resources Research, 2007, 43(6): W06413.
10.1016/S1001-6058(11)60381-9
 水動(dòng)力學(xué)研究與進(jìn)展 B輯2013年3期
水動(dòng)力學(xué)研究與進(jìn)展 B輯2013年3期
- 水動(dòng)力學(xué)研究與進(jìn)展 B輯的其它文章
- Experimental hydrodynamic study of the Qiantang River tidal bore*
- Numerical simulation of scouring funnel in front of bottom orifice*
- Evaluation of suspended load transport rate using transport formulas and artificial neural network models (Case study: Chelchay Catchment)*
- Simulation of water entry of an elastic wedge using the FDS scheme and HCIB method*
- Application of signal processing techniques to the detection of tip vortex cavitation noise in marine propeller*
- Analysis and numerical study of a hybrid BGM-3DVAR data assimilation scheme using satellite radiance data for heavy rain forecasts*
