陶慶云

?

基于多重網(wǎng)格的模擬退火算法

陶慶云*

(湖南文理學(xué)院 數(shù)學(xué)與計(jì)算科學(xué)學(xué)院, 湖南 常德, 415000)

為了提高模擬退火算法的收斂速度, 提出了一種基于多重網(wǎng)格的模擬退火算法(SAM), 用于求解高維函數(shù)優(yōu)化問(wèn)題, 并分析了其收斂性. 13個(gè)著名的測(cè)試函數(shù)對(duì)SAM算法進(jìn)行數(shù)值實(shí)驗(yàn), 結(jié)果表明SAM算法具有良好的搜索能力和收斂速度.

模擬退火算法; 多重網(wǎng)格法; 函數(shù)優(yōu)化問(wèn)題

模擬退火算法(Simulated Annealing)[1]在1982年由Kirkpatrick等人首次提出, 是一種基于Monte Carlo迭代求解法的啟發(fā)式隨機(jī)搜索算法. 它能夠有效的避免局部搜索算法易陷入局部最優(yōu)的通病, 是一種和遺傳算法一樣被廣泛應(yīng)用的優(yōu)秀全局搜索算法. 然而理論研究表明模擬退火算法實(shí)現(xiàn)全局收斂的時(shí)間性能很差[2], 大量實(shí)驗(yàn)也表明在求解高維函數(shù)優(yōu)化問(wèn)題時(shí)其搜索能力非常有限.

多重網(wǎng)格法[3]被認(rèn)為是求解偏微分方程組收斂速度最快的數(shù)值方法之一. 它由多層粗細(xì)不同的網(wǎng)格組成, 在粗網(wǎng)格上, 數(shù)值算法快速收斂, 但解的質(zhì)量較差, 在細(xì)網(wǎng)格上算法收斂到高精度的解, 但收斂速度較慢. 粗細(xì)網(wǎng)格的結(jié)合, 使得數(shù)值算法能以較短的時(shí)間收斂到高精度的解. 已有不少研究者將多重網(wǎng)格法與智能算法相結(jié)合用于求解復(fù)雜函數(shù)優(yōu)化問(wèn)題[4—6]等, 文獻(xiàn)[6]詳細(xì)討論了多重網(wǎng)格法與演化算法結(jié)合的應(yīng)用模式及其收斂性. 本文提出了一種基于多重網(wǎng)格的模擬退火算法, 以文獻(xiàn)[6]中13個(gè)著名的測(cè)試函數(shù)為例對(duì)SAM算法進(jìn)行數(shù)值實(shí)驗(yàn), 其中函數(shù)的變量個(gè)數(shù)均為30, 結(jié)果表明多重網(wǎng)格法能有效提高模擬退火算法的搜索能力和收斂速度.

1 多重網(wǎng)格法

考慮函數(shù)優(yōu)化問(wèn)題:

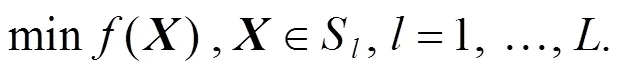
2 基于多重網(wǎng)格的模擬退火算法

下面給出基于多重網(wǎng)格的模擬退火算法流程:

Begin:

Initialize;

Restriction();

While not termination condition;

For2 i=0 to Markov chain length L do

Generate a new solution;

Evaluate new solution, calculate the difference df;

If df>0 or (df<0 and exp(-df/T)>rand(0,1) )

Accept the new solution;

Else

Accept the old one;

For3 three components of variable do

Simulated annealing;

End of for3

End of for2

End of while

End of for1

End

下面分析SAM算法的收斂性: 首先, 算法的搜索始終保持在網(wǎng)格上, 從一個(gè)初始狀態(tài)開(kāi)始后, 每一步狀態(tài)轉(zhuǎn)移都是在當(dāng)前狀態(tài)的臨域中隨機(jī)產(chǎn)生新?tīng)顟B(tài), 然后以一定概率接受, 接受概率僅依賴(lài)于新?tīng)顟B(tài)和當(dāng)前狀態(tài), 并由溫度加以控制. 因此, SAM算法對(duì)應(yīng)一個(gè)有限狀態(tài)馬氏鏈. 在每一溫度下, 算法充分遍歷, 計(jì)算馬氏鏈的變化直至平穩(wěn)分布, 從而SAM算法屬于時(shí)齊算法. 這說(shuō)明在每層網(wǎng)格上SAM算法都以概率1收斂到全局最優(yōu)解.

3 數(shù)值實(shí)例

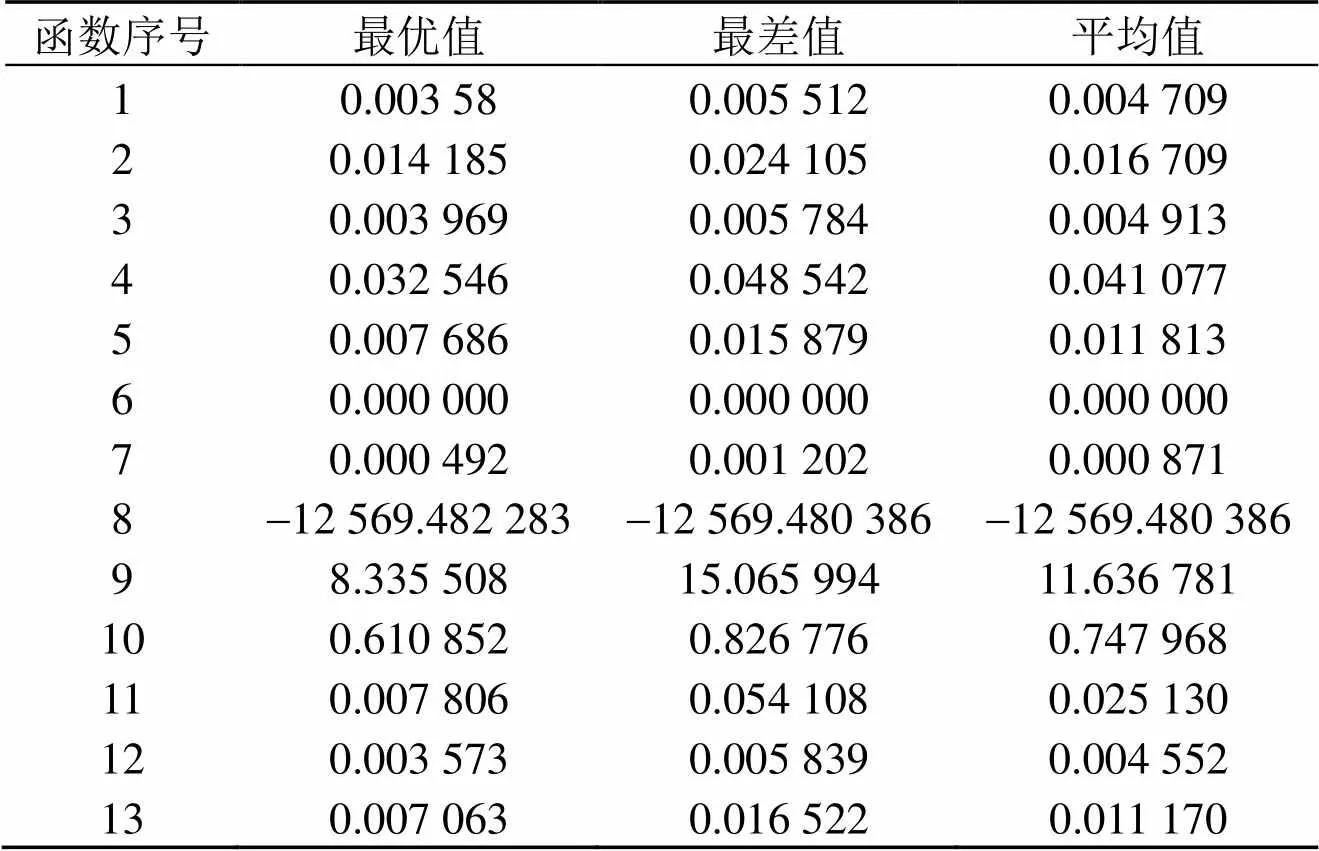
表1 算法運(yùn)行結(jié)果

4 結(jié)論

本文提出了一種基于多重網(wǎng)格的模擬退火算法, 實(shí)驗(yàn)結(jié)果證明SAM算法比傳統(tǒng)的SA算法搜索能力顯著提高, 參見(jiàn)文獻(xiàn)[2]中SA算法結(jié)果. 與文獻(xiàn)[6]中結(jié)果具有可比性. 這說(shuō)明多重網(wǎng)格法能有效提高模擬退火算法的搜索能力和收斂速度. 值得注意的是多重網(wǎng)格法并非一種獨(dú)立的搜索算法, 它具有很多種形式[9], 應(yīng)該與智能算法或數(shù)值算法完美結(jié)合才能更好的為人們所用.

附錄: 測(cè)試函數(shù)

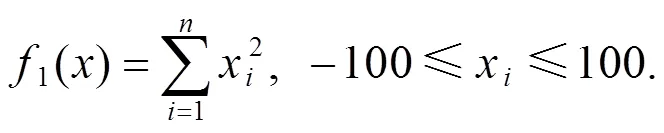
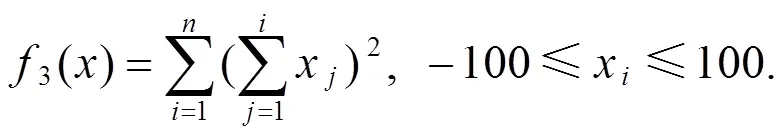
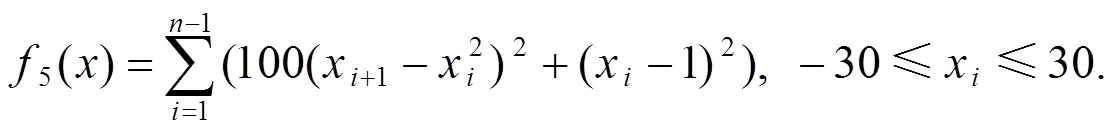
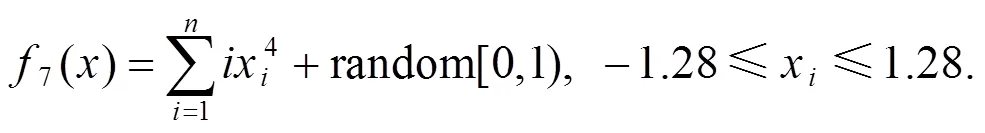
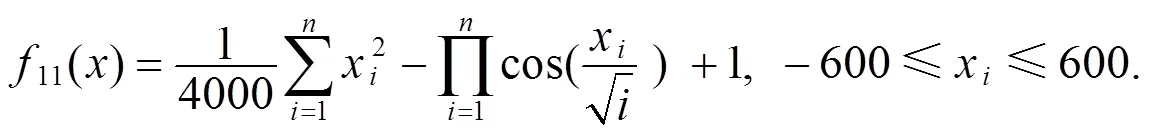
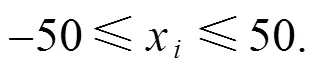
[1] 康立山. 非數(shù)值并行算法–模擬退火算法[M]. 北京: 科學(xué)出版社, 1998.

[2] 王凌. 智能優(yōu)化算法及其應(yīng)用[M]. 北京: 清華大學(xué)出版社, 2010.

[3] Hackbusch W. Multigrid Methods and Applications[M]. Berlin: Springer-Verlag, 1985.

[4] Brandt A, Ron D. Multigrid solvers and multilevel optimization strategies[M].Boston: Kluwer Academic Publishers, 2003: 1—69.

[5] Gelman E, Mandel J. Multilevel algorithms for optimization problems[J]. Math Progr Ser B, 1990, 48: 1—18.

[6] He Jun, Kang Lishan. A mixed strategy of combining evolutionary algorithms with multigrid methods[J]. International Journal of Computer Mathematics, 2009, 86(5): 837—849.

[7] Dong H, He J, Huang H, et al. Evolutionary programming using a mixed mutation strategy[J]. Inform Sci, 2007, 177(1): 312—327.

[8] Lee C Y, Yao X. Evolutionary programming using mutations based on the Levy probability distribution[J]. IEEE Trans Evol Comput, 2004, 8(1): 1—13.

[9] 李曉梅, 莫?jiǎng)t堯. 多重網(wǎng)格算法綜述[J]. 中國(guó)科學(xué)基金, 1996, 10(1): 4—11.

Simulated annealing based on multigrid

TAO Qing-yun

(College of Mathematics and Computer Science, Hunan University of Arts and Science, Changde 415000, China)

Multigrid methods have been proven to be an efficient approach in accelerating the convergence rate of numerical algorithms for solving partial differential equations. In order to accelerate the convergence rate of simulated annealing, a novel simulated annealing based on multigrid is proposed and its convergence is proven. The algorithm is tested on a set of 13 well-known benchmark functions. Experiment results demonstrate that multigrid methods can accelerate the convergence rate of Simulated Annealing, and improve their performance.

Simulated Annealing; Multigrid; Function optimization.

10.3969/j.issn.1672-6146.2013.04.002

O 241.8

1672?6146(2013)04?0008?04

email: 17734524@qq.com.

2013-09-28

(責(zé)任編校:劉曉霞)