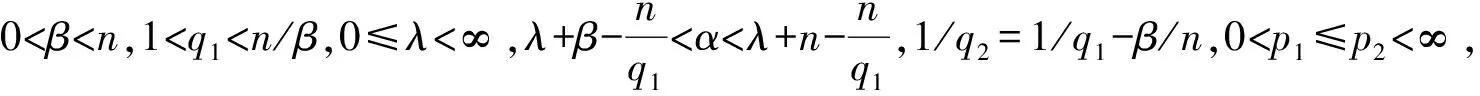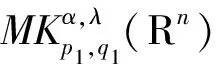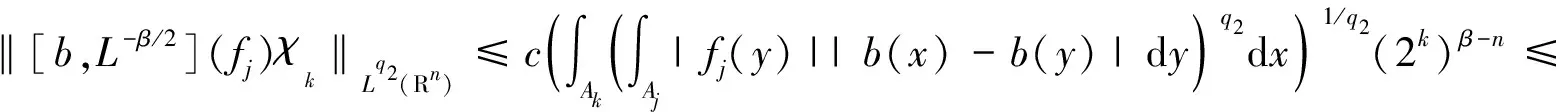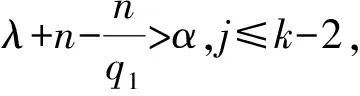交換子在齊次Morrey-Herz空間上的有界性
楊明華,張學銘,劉冬華
(暨南大學數(shù)學系,廣東 廣州 510632)
0 引言
定義一個二階散度型橢圓算子Lf=-div(Af),A=A(x)是指一個定義在Rn上的復的L∞系數(shù)的n×n矩陣,且滿足一致性橢圓條件:存在0<λ≤γ<∞,使得其中ζ,ζ∈Cn.
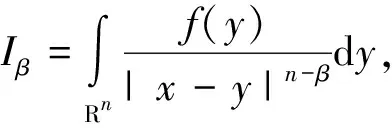
(0.1)
當L=-Δ即為Rn上的Laplace算子時,以上廣義分數(shù)次積分算子就是經(jīng)典的分數(shù)次積分算子.相應(yīng)的廣義分數(shù)次積分算子與BMO(Rn)函數(shù)b(x)生成的交換子[b,L-1/2]定義為:
[b,L-β/2](f)(x)=b(x)L-β/2(f)(x)-L-β/2(bf)(x)
(0.2)
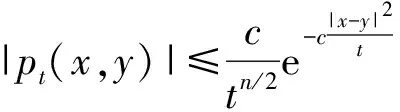
(0.3)
眾所周知,分數(shù)次積分算子是調(diào)和分析中以偏微分方程為背景的一種重要算子.在偏微分方程中為了研究Possion方程,Sobolve[1]引入經(jīng)典的分數(shù)次算子又稱Riesz位勢算子Iβ.1982年,Chanillo[2]引入了分數(shù)次交換子,并證明當b∈BMO(Rn)時,交換子[b,Iβ]是(Lp(Rn),Lq(Rn))型的,其中1/p=1/q-1/n.1998年Fan Dashan等[3-4]給出了奇異積分算子及其交換子在Morrey空間上的有界性,2004年Duong等[5]給出了廣義分數(shù)次積分算子交換子[b,L-β/2]從Lp(Rn)到Lq(Rn)是有界的.Lu Shanzhen等[6-8]在研究奇異積分算子時引入一類與PDE相關(guān)的比Herz空間和Morrey空間更一般的齊次Morrey-Herz 空間, 這類函數(shù)空間受到人們的重視, 得到了許多算子及交換子在其上有界性的結(jié)果, 受上述工作的啟發(fā), 考慮到與二階散度型橢圓算子L相關(guān)的廣義分數(shù)次積分算子交換子是否在齊次 Morrey-Herz空間上有界.本文中討論了這個問題,得出廣義分數(shù)次積分算子交換子[b,L-β/2]在Morrey-Herz空間上是有界的.
在敘述主要結(jié)果之前,給出一些必要的記號,Bk=(0,2k)={x∈Rn:|x|≤2k},Ak=Bk/Bk-1,k∈Z,χk=χAk,其中χAk表示Ak的特征函數(shù),c表示不同的常數(shù).
1 預備知識
定義1.1[6]設(shè)α∈R,λ≥0,0 (1.1) (1.2) (1.3) 引理1.2[5]假設(shè)條件(0.3)式成立,設(shè)0<α ‖[b,L-β/2](f)‖Lq(Rn)≤c‖b‖*‖f‖Lp(Rn). 引理1.3[9]設(shè)b∈BMO(Rn),?k,j∈Z,k≥j,則|bk-bj|≤c(k-j)‖b*‖. 本文中主要獲得定理: 對于K,由引理1.2知[b,L-β/2]從Lq1(Rn)到Lq2(Rn)是有界的,得到 對于J,當x∈Ak,j≤k-2,y∈Aj,有 2k-2≤|x-y|≤2k+1, 根據(jù)Minkowski和H?lder不等式以及引理1.3,我們得到 再利用引理1.1和引理1.3我們得到 cb*2kn/q2·2jn(1-1/q1)‖fj‖Lq1(Rn)+c2kn/q2·2jn(1-1/q1)‖fj‖Lq1(Rn)(k-j)b*+ cb*2kn/q2·2jn(1-1/q1)‖fj‖Lq1(Rn)≤c(k-j)b*2kn/q2·2jn(1-1/q1)‖fj‖Lq1(Rn), 于是得到 (2.1) 類似于J估計過程對H進行估計. ‖[b,L-β/2](fj)χk‖Lq2(Rn)≤ 根據(jù)Minkowski和H?lder不等式以及引理1.1利用引理1.3我們得到 b*2kn/q2·2jn(1-1/q1)‖fj‖Lq1(Rn)+2kn/q2·2jn(1-1/q1)‖fj‖Lq1(Rn)(j-k)b*+ b*2kn/q2·2jn(1-1/q1)‖fj‖Lq1(Rn)≤c(j-k)b*2kn/q2·2jn(1-1/q1)‖fj‖Lq1(Rn), 于是我們得到估計 cb*(j-k)2(k-j)(n/q1-β)‖fj‖Lq1(Rn) (2.2) 綜合J,H,K的估計我們得到 ‖ 證畢. [1] Stein E M.Singular integrals and differentiability properties of functions[M]. Princeton New Jersey:Princeton University Press, 1970. [2] Chanillo S. A note on commutators[J]. Indiana Univ Math, 1982,31:7-16. [3] Fan Dashan,LU Shanzhen,YANG Dachun.Regularity in Morrey spaces of strong solutions to nondvergence elliptic equations with VMO Coefficients[J].Georgian Math,1998(5):425-440. [4] Fan Dn,LU Shanzhen,YANG. Boundedness of operators in Morrey spaces on homogenous spaces and its applications[J].Acta Math Sinica(N.S) SUPPL,1998,14:625-634. [5] Duong X T, Yan L X.On commutators of fractional integrals[J]. Soc Math American,2004,132:35-49. [6] Lu Shanzhen,Xu Lifang.Boundedness of rough singular integral operators on the homogeneous Morrey-Herz spaces[J].Hokkaido Math J,2005,34(2):299-314. [7] Lu Shanzhen, Yang Dachun,Zhou Zusheng.Sublinear operators with rough Kernel on generalized Morrey spaces[J].Hokkaido Math J,1998,27(1):219-232. [8] Lu shanzhen,Tang Lin,Yang Dachun. Boundedness of commutatots on the homogeneous Herz spaces[J].Sci China Ser A,1998,41(10):1023-1033. [9] Lu Shanzhen, Yang Dachun. The continuity of commutators on Herz-type Spaces[J]. Michigan Math, 1997,44(2):255-280. [10] Yang Dachun,Zhang Pu,Tang Canqin.Bounded of generalized fractional integral operators[J].Approx Theory & Its Appl,2002,18:34-54.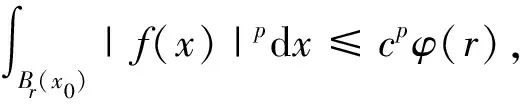
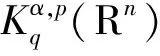
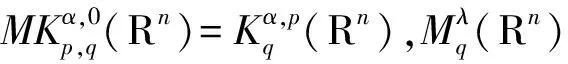
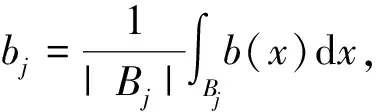
2 主要定理