TANG Zi-kai, HOU Yao-ping

?

Note on the augmented eccentric connectivity index

TANG Zi-kai, HOU Yao-ping

(Department of Mathematics, Hunan Normal University, Changsha 410081, China)

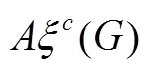
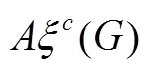
1 Introduction

All graphs in this article are simple and finite. The vertex and edge sets of a graphare() and(), respectively. The degree of a vertexinis denoted by deg() or() for short. The number of vertices ofis denoted by() and it is called the order of. The distanced(,) between two verticesand∈() is the number of edges on a shortest path connectingandin. The eccentricity of a vertexin(); denoted bye() or(), is defined to be max{d(;)|∈}.

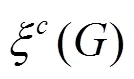
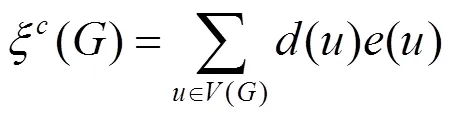
where the summation goes over all vertices of. In [2–6], Gutman et al. gave some mathematical properties of this invariant of graph.

The augmented eccentric connectivity index is an adjacency-sum-distance based index and it is defined as the summation of the quotients of the product of adjacent vertex degrees and eccentricity of the concerned vertex, for all the vertices in a hydrogen-suppressed molecular graph[3]. It is expressed as:

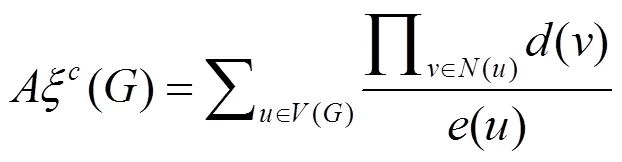
where the summation goes over all vertices of.

2 The augmented eccentric connectivity index of trees

First we consider the graph1and graph2depicted in Fig.1. These two paths differ only vertex label. In what follows we assume that≥≥1.

Fig.1 Two Paths (a≥b≥1)

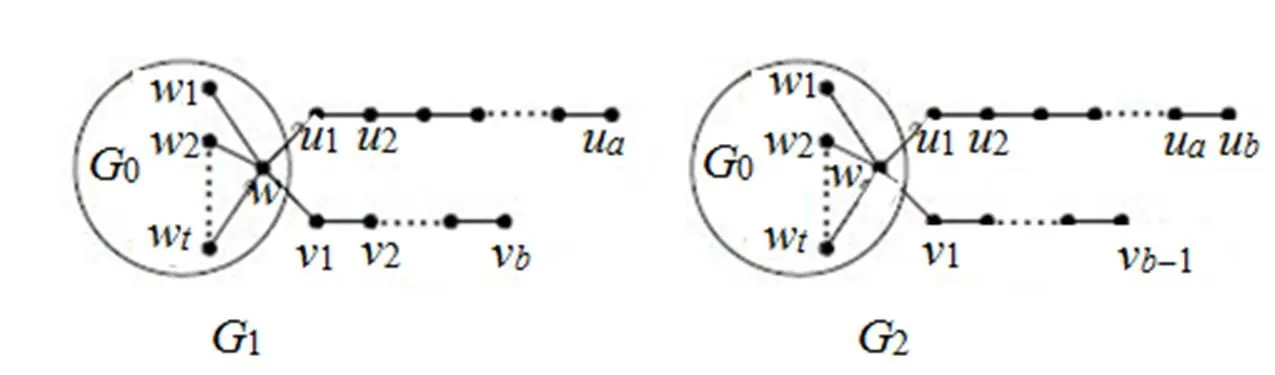
Fig. 2 The transformationG1→G2.

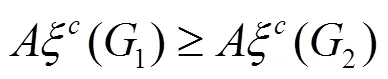
By Proposition 2.2, we obtain next proposition easily.

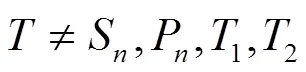
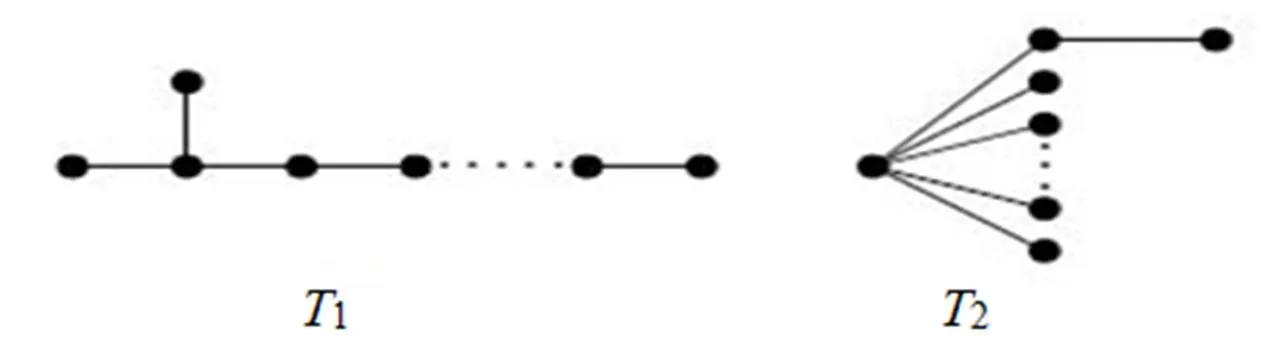
Fig. 3 Two trees T1, T2

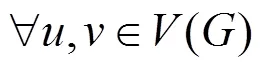
3 The unicyclic graphs with maximum the augmented eccentric connectivity index

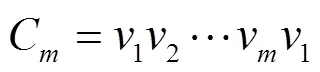
There is at last a number equal or greater than zero between1and2.

Fig. 4 The transformations Tr1, Tr2.

By Lemma 3 and 4, we have:

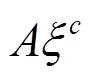
[1] Sharma V, Goswami R, Madan A K. Eccentric connectivity index: A novel highly discriminating topological descriptor for structure-property and structure-activity studies[J]. J. Chem Inf Comput Sci,1997, 37: 273-282.

[2] Ilic A, Gutman I. Eccentric Connectivity Index of Chemical Trees[J]. MATCH Commun Math Comput Chem, 2011, 65: 731-744.

[3] Bajaj S, Sambi S S, S. Gupta, A K. Model for prediction of anti-HIV activity of 2-pyridinone derivatives using novel topolo- gical descriptor[J]. QSAR Comb Sci, 2006, 25: 813-823.

[4] Doslic T, Graovac A, Ori O. Eccentric Connectivity Index of Hexagonal Belts and Chains[J]. MATCH Commun Math Com- put Chem, 2011, 65: 745-752.

[5] Zhou B, Du Z. On eccentric connectivity index[J]. MATCH Commun Math Comput Chem, 2010, 63: 181-198.

[6] Morgan M J, Mukwembi S, Swart H C. On the eccentric connectivity index of a graph[J]. Discrete Mathematics, 2011, 311:1229-1234.

圖的擴展離心連通指數(shù)

湯自凱, 侯耀平

(湖南師范大學(xué) 數(shù)學(xué)與計算機科學(xué)學(xué)院, 湖南 長沙, 410081)

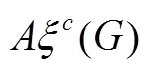
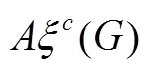
O 221.1

1672-6146(2012)01-0024-04

10.3969/j.issn.1672-6146.2012.01.007

2012-03-18

湖南省教育廳科研項目(08C579).

湯自凱(1973-), 男, 博士, 副教授, 研究方向為圖論及其應(yīng)用. E-mail: zikaitang@163.com

(責(zé)任編校:劉剛毅)