Retrospect and Perspective of Micro-mixing Studies in Stirred Tanks*
CHENG Jingcai (程景才), FENG Xin (馮鑫), CHENG Dang (程蕩) and YANG Chao (楊超)**
Key Laboratory of Green Process and Engineering, Institute of Process Engineering, Chinese Academy of Sciences,Beijing 100190, China
1 INTRODUCTION
Stirred reactors are widely encountered in chemical and metallurgical industries, since they can provide excellent mixing performance for gas dispersion,solid suspension and chemical reaction. The interaction of rotating impellers with stationary baffles produces complex and highly 3 dimensions turbulent flow with quasi-periodicity. Modeling of reactive flows is an arduous task due to its high inter-disciplinarity, for example, good understandings of turbulence (more often in multiphase systems), mixing, chemistry, and particularly the interaction among them are necessary.
Mixing is an important elementary process in chemical engineering, and its effect is especially demonstrated when scaling up equipments involved with chemical reactions. For many reactions in a bench-scale vessel, strong stirring is easily available to guarantee good mixing, however, for commercial scale units,mixing problems are most likely encountered and sometimes can be severe. This is because that the local hydrodynamics in industrial vessels may be very different from that in smaller ones, and the mixing time is typically much larger, making the same reactions more difficult to reach the technico-economical specifications available in bench-scale devices. Hence, the key factor is the mixing, in particular the mixing on micro-scales. Intensive studies on mixing, especially on micro-mixing, in stirred tanks are of great significance to the design, optimization and scale-up (or scale-down) of this type of reactors.
Assuming that species A and B are fed into a tank separately to react to form R, i.e., AB R+→ , all the states of mixing before the reaction occurs to a meaningful degree are summarized in Fig. 1, whether or not they are realistic. The most desired state is the well macro-mixed and well micro-mixed [Fig. 1 (a)],which may exist for very slow reacting systems. For the poorly macro-mixed and totally segregated [Fig. 1(b)], reactions cannot take place at all. The well macro-mixed and partially segregated state [Fig. 1 (c)]is physically unrealistic as the macro-mixing time is generally larger than that of micro-mixing, however it is commonly used to derive micro-mixing models in a Lagrangian framework. The poorly macro-mixed and well micro-mixed state [Fig. 1 (d)] cannot exist since well micro-mixedness certainly ensures well macromixedness. However, it was commonly used in the RTD (residence time distribution) theory. For many fast or quasi-instantaneous reactions, the most likely state is the poorly macro-mixed and partially segregated [Fig. 1 (e)], for which the spatial distribution of species average concentrations and the degree of segregation must be described properly.
In reactive flow systems, the importance of mixing can be best represented by comparing its characteristic time scales with those of chemical reactions [1].As illustrated in Fig. 2, the largest flow time scale is the recirculation time tcir, which lies generally between the average residence time tresand the turbulence integral time scale tu, and the smallest one is the Kolmogorov time scale tη. The time scale of macro-mixing tmacrois generally equivalent to tcir(if dead zones exist,tmacromay be one magnitude larger than tcir), and that of micro-mixing tmicrois generally on the same magnitude with tu. Thus, mixing is closely related to the flow. Based on the relationship between the time scales of reactions and flows, reactive flow systems can be roughly classified into three zones, i.e., the kinetics-controlling zone, the overlapping zone and the mixing-controlling zone, as shown in Fig. 2.

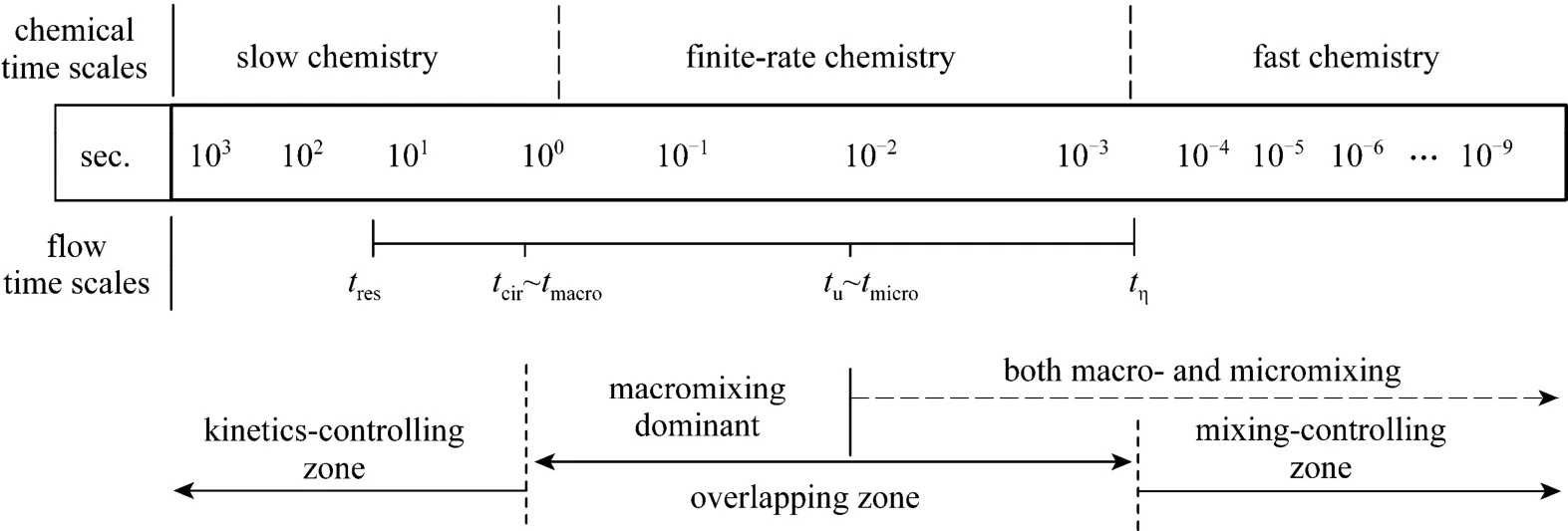
Figure 2 Characteristic time scales of chemical reactions and typical turbulent flows (The rows illustrating the chemical and flow time scales are from Fox [1], and the last row of mixing zones is added in this work)
Mixing and flow are of little importance in the kinetics-controlling zone, since the reagents have sufficient time to mix completely before the reactions can proceed to any significant degree. For a large class of reactions, whose some or all of the reaction time scalestklie belowtmicro, both chemical kinetics and mixing are important, and reactions may become purely controlled by mixing especially micro-mixing whentk?tmicro. Many fast or quasi-instantaneous reactions fall into this class, such as many inorganic reactions, pharmaceutical precipitations, free radical polymerizations,etc. For these reactions, micro-mixing can significantly change product properties and quality,such as crystal size distribution (CSD) and the molecular mass distribution of polymer molecules. Taking the self-developed production technology of butadiene rubber (BR) in China as an example, although the technique has been greatly improved through years of development, many problems still exist in the quality of BR, such as high content of micro-gel, low molecular mass and high degree of branching [2].A main reason is the micro-mixing between the initiator and monomers. Poor micro-mixing might produce more undesired by-products for organic reactions accompanied by side-reactions, leading to higher purification costs.
Micro-mixing refers essentially to the finest scale of mixing,i.e., mixing on the molecular scale. From the initial scale of feeding species to the final molecular scale, mixing proceeds actually in a cascade way.However, different stages and sub-processes of mixing,e.g., large-, meso- and small-scale mixing, have been used to interpret the mechanisms of micro-mixing.Taking a Lagrangian perspective, and by assuming ideal homogeneous large-scale mixing, Pohorecki and Baldyga [3] introduced a spectral interpretation of small-scale mixing that distinguished different mechanisms at different subranges of eddy size (Fig. 3). Three subranges of small-scale mixing,i.e., inertial-convective(kC<k<kη), viscous-convective (kη<k<kB) and viscous diffusive (k>kB) subranges, can be distinguished.
These three subranges correspond to different mechanisms of small-scale mixing, such as the disintegration of large concentration eddies (Lη<L<LC), the viscous deformation (LB<L<Lη) and the accelerated molecular diffusion due to deformation (L<LB). Another important aspect of micro-mixing mechanisms is engulfment [4, 5], which describes the stretching process of vortex tubes of scaleLωaccompanied by the incorporation of fluid from the surrounding environment. Engulfment, deformation and molecular diffusion constitute the micro-mixing process, leading to homogeneity of local concentrations on the molecular level. Although the random process of molecular diffusion is the only effective approach to accomplish the molecule-scale mixing, small-scale processes such as engulfment and viscous deformation are usually considered to be more important aspects of micro-mixing.Determining the controlling mechanism of micromixing is important when formulating a micro-mixing model, as the full mechanism of micro-mixing is complex to be formulated mathematically and very difficult to be solved.
Large-scale mixing is best described with CFD in a Eulerian framework, whereas micro-mixing is better explained taking the Lagrangian perspective as shown above. Thus, an attempt to give an integral description of all mixing scales,i.e., from the reactor scaleLRto the molecular scale, is made here and illustrated in Fig. 4.

Figure 3 Schematic of turbulent kinetic energy E(k) and concentration fluctuation spectrum G(k) (log-log scale) [3]
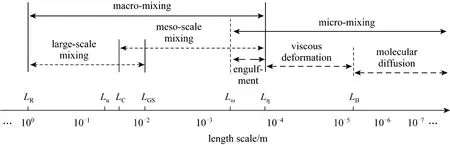
Figure 4 Schematic of length scales of different sub-processes of mixing
In CFD simulations, large-scale mixing covers the scales fromLRto the average grid sizeLGS.Meso-scale mixing covers scales fromLCtoLη, referring particularly to the plume of fresh feed [6].Through large- and meso-scale mixing, the spatial inhomogeneity of the average concentration (averaged over a grid cell) over the reactor is greatly reduced.The term meso-mixing is originally used to describe in a Lagrangian framework how the fresh feed stream develops from its initial scaleLOCto the scale close to or belowLη. However, in the CFD and by employing finer grids around the feeding point, the concentration distribution of fresh feed can also be well obtained.Thus, meso-mixing can be classified into macro-mixing from the CFD perspective now.
2 MICRO-MIXING EXPERIMENTS
2.1 Single phase systems
Micro-mixing experiments have been commonly carried out with selected chemical test reactions,e.g.,consecutive competing or parallel competing reactions.The most frequently used consecutive competing reaction system may be the diazo coupling between 1- or 2-naphthol and diazotized sulphanilic acid developed by the group of Bourne [7]. The neutralization and alkaline hydrolysis of ester [8] and the iodide/iodate reaction scheme [9] are two most commonly used parallel competing test reactions. Each system has its own limitations, such as the side reactions and the temperature-sensitive reagents of the diazo coupling,the low solubility of ethyl chloroacetate,etc. Guichardonet al. [10] compared experimentally two most currently used test reactions,i.e., the iodide/iodate and the diazo coupling, in detail on comprehensive criteria such as easy handling, quick analysis, sensitivity to micro-mixing effects, stability of reaction products,good measurement reproducibility and toxicity. By these criteria, neither was perfect, and each had its own strong points. Due to the easy processing, the iodide/iodate system was very flexible for many types of mixers (batch, semi-batch or continuous mixers).The application of the diazo coupling is not recommended by the present authors.
Concerning the test reactions, further work is apparently needed to meet all the criteria mentioned above. Moreover, the present test reactions are generally applicable only to the systems operated under mild conditions,e.g., at ambient temperature and under normal pressure. Therefore, some new systems which can be applied to the systems with high temperature and/or pressure should also be developed.Besides, the suitable test reaction is urgently needed for two-phase and multiphase systems and we will address later on this challenge.
By measuring the distribution of undesired secondary product in a test reaction, the micro-mixing efficiency is commonly quantified by the normalized segregation indexXS(orXQ), which varies between 0(ideally mixed) and 1 (totally segregated). Apparently,the higher theXSis, the poorer the micro-mixing efficiency.XSis significantly affected by the fluid dynamics in the reactors. Some variables, such as feeding location, impeller type and position, agitation speed, and the feeding schedule of the limiting reactant have been shown to alter significantly the value ofXS. Generally,XS(orXQ) decreases with feeding time and finally comes to an asymptotic value (Fig. 5) [11].Local turbulence energy dissipation rateεis the key physical parameter to micro-mixing. Largerεleads to better micro-mixing efficiency. Higher stirred speed increases the mean dissipation rateε, and so is the local value ofε. Thus,XSdecreases with increasing stirred speeds (Fig. 6) [11]. In stirred reactors,εin the impeller discharge region is usually 2-3 orders of magnitude larger than that in the top surface region.Hence,XSwill decrease significantly from a position far away from the impeller to a position very close to the impeller (Fig. 6). And under certain conditions,like feeding in the trailing vortex (assuming no backmixing) generated by a Rushton turbine using pipes rotating with the impeller,XScan be reduced even by 7-fold [12].
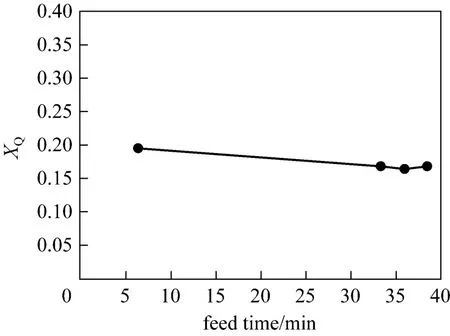
Figure 5 Influence of feeding time on XQ (feed point F1,N=200 r·min-1)[11]

Figure 6 Influence of impeller speed on XQ (F1 is on the surface, F3 is close to the impeller and F2 lies between F1 and F2) [11]
Micro-mixing experiments in single-phase stirred vessels have been conducted extensively in the literature and valuable data have been documented. Future work in this aspect should be focused on the systems with multi-impellers, new impeller types and special conditions such as boiling. Also, feeding in the impeller region is still worth in-depth studies because accurately measuring and predicting turbulent quantities in this region may be still challenging.
2.2 Multiphase systems
The multiphase reactive systems discussed in this work refer to the case in which reactions only occur in the continuous phase, or the dispersed particles are inert. Micro-mixing in multiphase vessels are certainly affected by a number of additional factors, such as density difference, fraction of the dispersed phase,particle size, gas flow rate, aggregation and breakup of bubbles or droplets, and even sphericity and hardness of solid particles. Moreover, detailed information on the impact of the dispersed phase on local ε of the continuous phase is necessary for studying multiphase micro-mixing. Thus, studies on multiphase micromixing focus mainly on two aspects: (1) measurement methods; (2) the impact of the dispersed phase on ε.The understanding of aspect (2) helps formulating multiphase micro-mixing models as well as conducting multiphase micro-mixing experiments. On the other hand, since local energy dissipation in multiphase systems with higher concentration of particles is hard to be obtained, the impact of the dispersed phase on ε can be acquired from improved measurement methods or reliable CFD of multiphase flows.
2.2.1 Solid-liquid systems
Villermaux and Fournier [9] were the first to use the iodide/iodate method to study the micro-mixing in a solid-liquid vessel. They found that micro-mixing efficiency was significantly increased by the presence of solids, though mean power consumption ε was not affected considerably by solids fraction up to 16% (by mass). The result is somewhat weird, thus after correcting for possible losses of iodine by evaporation during filtration [13], the authors found that the effect of solids on micro-mixing was negligible for up to 6%(by mass) and the diameters ranging from 27 to 1250 μm. Again, no influence of solids up to 16% (by mass)on
ε was found by Barresi [14], who reported that at relative low solid concentrations [<7% (by volume)]and with intermediate sizes of glass beads micromixing was basically unaffected.
In the very recent micro-mixing experiments conducted by Hofinge et al. [15], torque measurements were employed to maintain ε of the suspension the same as that in single-phase cases. Micro-mixing efficiency was not affected by the presence of glass particles (500 μm) up to 2.5% (by mass) when feeding both close to and far from the impeller. And at 11.63%(by mass) of particles, solid cloud formation was observed. The micro-mixing efficiency was decreased by the solid cloud, and when feeding into the clear layer,the decrease was much more considerable. The micro-mixing studies at higher concentrations where cloud formation occurred have also been carried out previously by Barresi [14, 16]. Still, the micro-mixing efficiency was greatly decreased by the solid cloud.However, the work on micro-mixing in the case of solid cloud formation is still limited, and apparently more in-depth and comprehensive work is needed.
Based on an extensive literature survey of experimental data in pipes and jets (generally air as the continuous phase), Gore and Crowe [17] concluded that turbulence intensity was suppressed (damping up to 50%) by small particles and increased (up to 360%)by larger ones. The ε in solid-liquid systems with low to intermediate loadings may not be influenced by the presence of particles, however, the distribution of local ε could be different from that of single-phase systems. The results of Guichardon et al. [13] are opposite to the criterion of Gore and Crowe [17], and hence more in-depth work considering the distributions of local ε and solid concentrations is needed.
Unadkat et al. [18] combined fluorescent particle image velocimetry (FPIV) and digital image analysis to characterize the hydrodynamics of a solid-liquid suspension stirred by a pitched blade turbine impeller.Solid particles of 1000 μm and with up to 0.5% (by volume) were used. The turbulence dissipation rate was suppressed by solid loading above 0.2% (by volume), and about a decrease of 21% was found in the discharge stream. Since the ratio of particle diameter to integral length scale was 0.285, the criterion of Gore and Crowe was not valid in this case. However, Montante et al. [19] showed good consistence with the criterion of Gore and Crowe. In this work,PIV was employed to measure the dissipation rate,and two sizes of particles, i.e., 115 and 774 μm, and solid loadings of 0.1% (by volume) and 0.2% (by volume) were investigated. Rather than measuring directly the dissipation rate, some researchers studied the impact of solid particles on turbulence in terms of RMS (root mean square) velocities, as well summarized by Hofinge et al [15]. In a word, great disagreement exists in the literature on the impact of the presence of solids on turbulence.
2.2.2 Gas-liquid and liquid-liquid systems
Micro-mixing studies in a gas-liquid vessel was also first conducted by Villermaux and Fournier [9],using the iodide/iodate method. They found that at constant speeds, micro-mixing efficiency decreased with the gas flow rate, whereas ε was lowered by bubbles. This is easy to be understood since sparging lowers the energy drawn from the impeller. At the same gas flow rate, micro-mixing efficiency increased with stirred speeds (Fig. 7) [20]. The iodide/iodate reaction scheme was also used by Lin and Lee [21] to investigate the micro-mixing in gas-liquid stirred vessels at higher flow rates [from 1.5 to 20 vvm (gas volume flow per unit of liquid volume per minute)].Improved micro-mixing was reported under most of conditions (such as different feed locations and speeds). Using the diazo-coupling reaction system,Brilmanet al. [22] investigated the influence of sparging and the changes in turbulent kinetic energy spectrum on the liquid micro-mixing. Generally, very limited influence of feeding positions and sparging from 0.5 to 10 vvm at constant stirred speeds on micro-mixing was reported.

Figure 7 Influence of impeller speed on XQ [20]■ single feed; ● double feed
With the torque measurements and by increasing stirred speeds to keepεthe same level for both sparging and unsparged cases, Hofingeet al. [15] investigated the micro-mixing at different feed locations and gas flow rates under non-flooded conditions. Micromixing was not affected by sparging up to 1.5 vvm near the impeller, but significantly improved near the top surface at higher gassing rates. Scattered data were obtained at the highest sparge rate of 1.5 vvm and the lowest value ofεdue probably to the facts of (1) the inaccuracy of torque measurements and (2) the increasing ratio of power from sparging gas to that input by the impeller especially when flooded, as mentioned also by Lin and Lee [21].
For some special gas-liquid systems, such as boiling and hot sparged stirred vessels, new test reaction systems have been developed to characterize liquid micro-mixing in such cases,e.g., a system comprising two parallel competitive reactions such as the precipitation of cupric hydroxide and the alkaline hydrolysis ofγ-butyrolactone [23]. Experimental results show that liquid micro-mixing in hot sparged and boiling systems was apparently improved due probably to the lower liquid viscosity and the strong bursting of vapour bubbles [23]. As in ambient temperature systems,feed location also has a significant effect on micro-mixing efficiency in hot and boiling systems.
The work on micro-mixing in liquid-liquid systems is very limited. The characterization of liquidliquid flow fields and turbulence levels is difficult.Moreover, the mean size and size distribution of drops are dependent on the configuration and operating conditions. On the other hand, the mixing in the dispersed phase is much more challenging than that in the continuous phase. Brilmanet al. [22] used the diazo-coupling reaction system to investigate the influence of drops and the changes in turbulent kinetic energy spectrum on micro-mixing. The effect of the delocalization of the reaction zone was observed by them due to naphthol extraction by the dispersed phase. They pointed out that in liquid-liquid systems, the knowledge of combined effect of mass transfer and mixing was highly desired. As for characterizing the flow fields and turbulence levels of both liquids, LIF (laser-induced fluorescence) combined with high-speed cameras could be a promising technique. And for the characterization of the micro-mixing in liquid-liquid systems, the systems involving the precipitation could be a choice, such as the precipitation of cupric hydroxide by Zhaoet al[23].
2.2.3Perspectives on multiphase micro-mixing
For multiphase systems, the dispersed phase brings new problems in the test reaction systems. For example, for the neutralization and alkaline hydrolysis of ester, the important product of ethanol could be significantly affected by bubbles,e.g., entrainment or absorption by bubbles. And for the iodide/iodate,losses of iodine by sublimation during filtration may also occur. Thus, multiphase micro-mixing experiments must be conducted with special carefulness. Generally,the iodide/iodate and diazo-coupling methods have been used in solid-liquid and gas-liquid systems. However, for three-phase systems or the systems with very high loadings, the reliability of these test reactions is questionable. Moreover, for liquid-liquid systems, the products of these two reactions may dissolve in the dispersed liquid, so new test reactions such as the precipitation may be a good choice.
Clearly, disparities and/or even contradictions between different studies on two-phase micro-mixing experiments and on the impact of the dispersed phase on turbulence exist widely. The reported studies are limited to a narrow range of particle sizes, concentrations and the configurations of the vessels. Moreover,the micro-mixing in the case of solid cloud formation needs much more in-depth and comprehensive work.For gas-liquid systems, the impact of sparging on micro-mixing both under flooded and non-flooded conditions is still unclear.
For the systems of intermediate or high particle loadings, although the distribution of the dispersed phase can be measured with some devices like PEPT(positron emission particle tracking), the turbulent quantities cannot be obtained to date. Ideally, multiphase CFD can obtain multiphase turbulence, the flow fields of all phases and the distributions of dispersed phases. However, this is still challenging for the following reasons: (1) since inter-phase turbulence transfer is still uncertain, multiphase turbulence models are generally extended from those of single phase,e.g.,the mixturek-εmodel; (2) for higher particle loading systems, particle-fluid and particle-particle interactions make simulations much more difficult; (3) presently used multiphase flow models lack rigorous and adequate experimental validation. Therefore, micromixing experimental research in multiphase systems needs to tackle more tasks compared to those in singlephase systems.
3 MICRO-MIXING MODELS AND SIMULATION
Fast and quasi-instantaneous reactions are closely related to mixing and local turbulent fluctuations.However, the attainment of homogeneity of concentrations on small scales must be achieved both by maximizing diffusion rates and by decreasing variations on larger length scales. Hence, for simulating reactive mixing accurately, each individual process and the interaction among them need to be modeled.Solving the governing equations for mass, momentum and species transport can achieve this purpose in principle, however, the very wide range of coexisting time and space scales make it numerically intractable. Thus,some approximated models must be employed.
3.1 Lagrangian micro-mixing models
Lagrangian micro-mixing models can be roughly classified into two subgroups: the empirical models which are based on the RTD theory and the concept of fluid environments, and the theoretical models which are based more on the turbulence theory such as the spectral analysis of turbulent kinetic energy and concentration fluctuation spectrum.
3.1.1 Empirical models
Based on the RTD theory, a host of empirical micro-mixing models have been proposed. Being consistent with the given RTD, two extreme limits of micro-mixing have been defined: total segregation and maximum mixedness. The micro-mixing states illustrated in Fig. 1 (b) and Fig. 1 (a) or Fig. 1 (c) correspond to the two limits. The CD (coalescence-redispersion)model is another type of RTD-based models [24].
Another class of empirical micro-mixing models is based on the concept of fluid environments. The composition space is commonly divided into a small number of environments (two, three or four) with each being in the state of maximum mixedness or complete segregation or certain status in between. Adjacent fluid environments interact with each other due to micromixing. Many multi-environment models have been developed and applied so far, such as two-environment(2E) models, 3E models and 4E models [25].
Empirical models have several shortcomings.The principal one is that the empirical or exchange parameters in these models are determined without firm physical basis, or even somewhat arbitrary.Moreover, they cannot predict the spatial distribution of scalar fields due to the assumption of well macromixedness, so how to fully validate the model predictions becomes a serious problem. Because of these weaknesses, their practical applications usually involve previous experimental identification of the system, which greatly limits their practical use. However,empirical micro-mixing models are still useful to a certain extent.
3.1.2 Theoretical models
Theoretical models are based more on turbulence theory or spectral theory. From the analysis of turbulent kinetic energy and scalar fluctuation spectra, the theoretical models try to distinguish different mechanisms of meso- and micro-mixing, and relate mathematically tmicroto turbulence and flow properties such as ε and μ.
An important class of turbulence theory-based models is the so-called diffusion models. Three kinds of diffusion models have been developed and summarized by Pohorecki and Baldyga [3]. Among those, the interaction by exchange with the mean (IEM) model[26] has been most widely used. The IEM model still finds some applications now, mainly in the coupling with CFD. The IEM model can be expressed by

where ciis the concentration of ‘points’, andic〈〉 the average concentration of the environment. The IEM model assumes the reactor is well macro-mixed,therefore, the determination of tmicrois difficult since tmicrois intimately related to the underlying flow field.Nevertheless, due to its simplicity, the IEM model has been applied to simple and complex chemical reactions to check for sensitivity to micro-mixing effects [27],and to precipitations to investigate the effect of micromixing on crystal sizes by Pohorecki and Baldyga [28].
The engulfment-deformation-diffusion (EDD)model that describes the full mechanism of micromixing was developed by Baldyga & Bourne [4, 29].The EDD model reflects the complete process of micro-mixing with relative all-sidedness, however, it is complicated and difficult to be solved due to its wide range of time and space scales. For not very high Schmidt numbers, e.g., Sc<4000, engulfment becomes the controlling mechanism of micro-mixing, and the full EDD reduces to the well-known engulfment model (E-model), into which the chemical kinetics can be directly incorporated [30]. Fig. 8 illustrates the process of eddy engulfment of turbulent activated vortices [4]. The E-model is given by
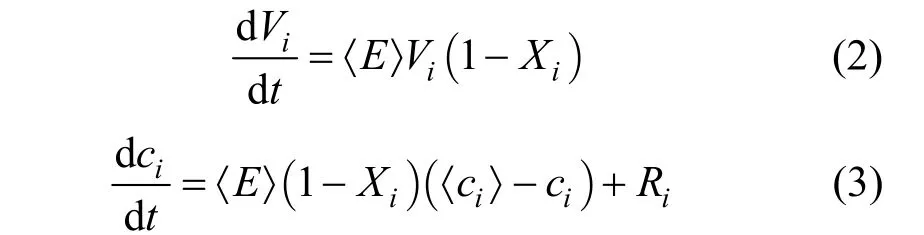
where E is the engulfment rate, E =0.0581/2,and Viand Xidenotes the volume and the local volume fraction of an i-rich region. Later, Baldyga et al. [31]proposed a modified E-model which accounts for mixing in the inertial convective range of the turbulent spectrum.

Figure 8 Schematic of the process of eddy engulfment of turbulent activated vortices [4]
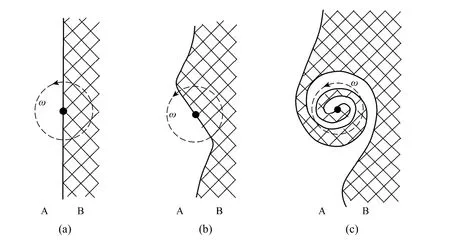
Figure 9 Schematic of the process of formation of an eddy-containing lamellar structure generated by engulfment [4]
The morphology or distribution of different material elements in the E-model was assumed to be a lamellar structure as shown in Fig. 9 (c) [4], in which equal volumes of environment fluid (A) and element(B) were distributed pseudo-periodically. The structure would change intermittently in step with the eddy lifetime. Based on high speed micro-photographic observations, Liet al. [32] found that slice-like and/or strip-like configurations rather than lamellar structures were more likely to form in the case of commonly encountered point source mixing. Grounded on the configurations, the authors proposed a new shrinkage slab (SS) model (Fig. 10) [32], which highlighted the role of shrinking deformation and/or the interaction between deformation and diffusion while excluding the relatively complicated engulfment step. Compared to the E-model, the SS model seemed more reasonable for the point source mixing and was expected to be applicable to broader Schmidt numbers [32, 33]. The expressions for the three models,i.e., the IEM model, the E-model and the SS model, are actually of the same form. Thus, these models are essentially equivalent in applications if the model parameters are suitably chosen.
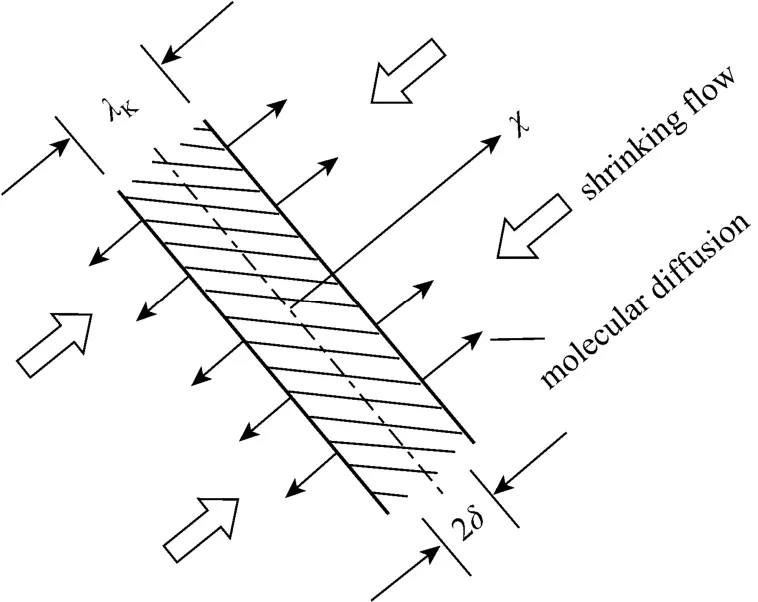
Figure 10 Schematic of a shrinkage-slab element [32]
As already discussed in the IEM model, a principal problem when utilizing Lagrangian micro-mixing models lies in the determination oftmicro, which is strongly dependent on the local flow field. As stated by Fox [1], the choice oftmicrois actually an essential ingredient in all approaches for modeling micro-mixing,and in many cases the choice oftmicrohas a much greater impact on the predicted product distribution than the choice of micro-mixing models. In deriving the theoretical models such as the EDD model and the E-model, the turbulence flow is assumed to be isotropic and homogeneous at very high Reynolds numbers. Thus, by utilizing the universal nature of this type of flow,tmicrocould be related to the turbulence time scale. Therefore,tmicrois generally of the following form:

For example, in the E-model,tmicrois given by

Actual flows are inhomogeneous, and even in very high Reynolds number flows, anisotropy exists everywhere, such as in the impeller region and in the large-scale eddies. Thus, for actual flows or many low and intermediate Reynolds number flows, Eqs. (4) and(5) could be not valid any more, and they may be dependent on Reynolds numbers. In addition to the determination oftmicro, another difficulty lies in how to determineε. In stirred reactors,εin the impeller discharge region is usually several orders (2-3) of magnitude larger than that in the top surface region. In applications of Lagrangian micro-mixing models, a spatially averagedεbased on ideal flows and experimental data is commonly employed. However, great uncertainties are unavoidable. Fig. 11 gives the simulated results of micro-mixing in a stirred tank with the E-model [11]. In the locations far from the impeller,adoptingεfrom CFD shows better agreement with experimental data, however, theεfrom empirical data shows better agreement in the impeller region.
Despite some limitations, the theoretical models,especially the E-model, have been widely used to describe fast simple and complex reaction schemes, and to predict mixing-precipitation processes [34, 35]. For describing macro-mixing more accurately, some empirical models or simple zone models were adopted.Baldygaet al. [34] developed a general mixingprecipitation model to describe the precipitation of BaSO4 in a double feed semi-batch. Micro-mixing was described by the E-model, and macro-mixing was described by using a simple loop plug flow model. A similar mixing-precipitation model was then applied by Phillipset al. [36] to a single-feed semi-batch precipitation process to describe the mixing effects on the final CSD and particle morphology. The E-model has also been coupled with CFD codes to give a more detailed description of flow fields. Ranade and Bourne[37] combined the E-model with a relatively simple CFD method to simulate consecutive competing reactions in a stirred tank, and the predictions showed good agreement with the experimental data. Akiti and Armenante [35] coupled the E-model with CFD to predict the final product distribution of fast parallel reactions in fed-batch stirred reactors, and good agreement between the experiments and the predicted results was also obtained.
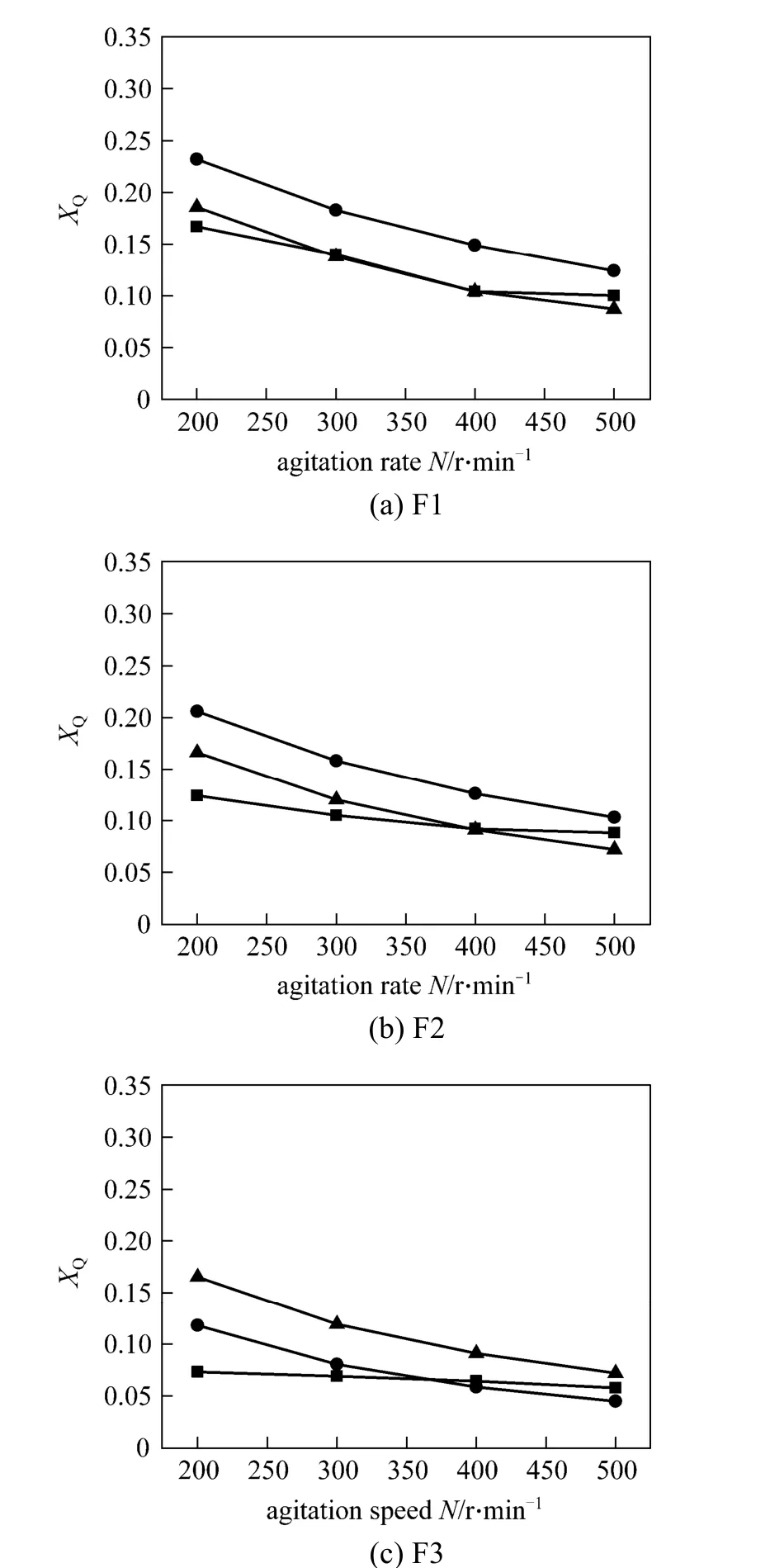
Figure 11 Experimental and simulation results of XQat feed points: F1, F2 and F3 (In Case 1, local turbulent dissipation is given by empirical data summarized in literature and in Case 2 it is given by CFD with the k-ε model) [11]■ exp.; ● Case 1 (simulation); ▲ Case 2 (simulation)
3.2 Eulerian micro-mixing models
Eulerian micro-mixing models are based on statistics. In a Eulerian framework, an averaging approach,e.g., the Reynolds averaging, is generally employed to solve instantaneous scalar transport equations. Taking a typical non-premixed single second-order reaction,ABR+→ , for example, the instantaneous scalar transport equation is expressed as

3.2.1Moment closure methods
A very simple but very widely used moment closure was presented by Toor [38] for single secondorder reactions:
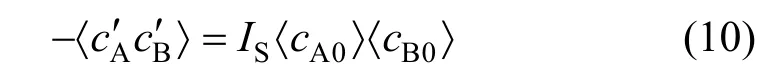
whereISis the intensity of segregation. Another similar model was developed by Patterson [39]:

In addition to oversimplification, these moment closures are generally only valid under very limited conditions,i.e., initial Gaussian PDF, symmetrical PDF distribution or specific reactant volume ratios [34].
Like the closure foriucα′〈 〉, a transport equation forABcc′′
〈 〉 can also be obtained and solved, however,it is very complicated and new unclosed third-order correlations are introduced. Work on extending moment closures to complex reactions has been reported,however, it is difficult and other closure problems will arise, and the reported results are in poor agreement with experimental data or simulations [40]. The popular moment closure for the scalar covariance is of very limited applicability [1], and is not applicable when complex reactions are to be modeled [34].
3.2.2PDF closure methods
The closure methods based on the joint scalar PDFare good alternatives:

Mainly two kinds of PDF methods have been proposed: the presumed-PDF method and the full or transported PDF method.
In the presumed-PDF methods, closure schemes must be employed to evaluate the average source term in Eq. (12). By using the mixture-fraction transformation technique, it is possible to describe and solve a turbulent reacting flow by a reduced set of scalars with their corresponding transport equations,i.e., the mean and the variances of a mixture-fraction vector,〈〉ξand, and of a reaction-progress vector, 〈〉Yand[1]. Molecular mixing is commonly described by the models extended from Lagrangian micro-mixing models, such as the multi-environment model and the E-model. Based on conditioning on the mixture fraction, the presumed-PDF methods assume some special shapes for the joint mixture fraction PDF to close ()Sα〈〉c. Many distribution functions have been proposed and applied, such as normal,β-PDF and multi-environment presumed PDF or finite-mode PDF (FM-PDF, assuming joint delta function distribution) methods [41]. Theβ-PDF and FM-PDF methods have been widely used in single and complex reactions and in precipitation processes [41, 42]. The presumed-PDF methods are implemented and solved with relative ease, and their incorporation into existing popular CFD models is straightforward. However,since they give a rough evaluation of a continuous PDF, they are not suitable for complex reacting systems or for the reactions with kinetics being sensitive to the shape of the joint PDF [43]. Another potentially serious problem is that though ()Sα〈〉ccan be closed easily with the presumed-PDF methods, the accuracy cannot be guaranteed. This was observed by ?ncület al. [44], who employed some conventional micro-mixing approaches such as the E-model and the FM-PDF method with two and three nodes to simulate the mixing-precipitation of BaSO4 in single-jet coaxial tubular reactors. It seems that some models showed drastic deviations from the experimental data in some cases,no model can give a perfect agreement with the experiments in all cases and configurations, and even under some conditions using no micro-mixing model gave better agreement with the experiments.
In the full-PDF methods, a transport equation forc(;,)
fcψxt at every point in the sample space can be obtained and then 〈Sα(c)〉 can be evaluated exactly without any closure schemes. However, this equation is somewhat complicated and involves unclosed terms,i.e., the conditional scalar Laplacian termwhich is expressed as
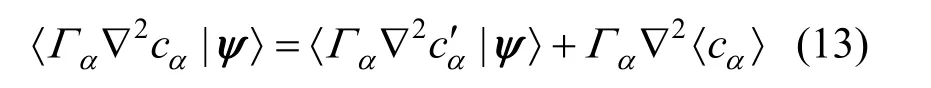
where the conditional scalar dissipation rate termis related to molecular diffusion and should be modeled using appropriate micro-mixing models. Referring to the models for closing〉, many have been used or proposed todate and they have been well summarized by Meyer and Jenny [45]. In addition to some conventional Lagrangian micro-mixing models like CD and IEM,many others have also been developed recently, such as mapping closure (MC) model, Fokker-Planck (FP)model, Euclidean minimum spanning tree (EMST)model and parameterized scalar profiles (PSP) model[46]. The advantages of the full-PDF methods are: (1)the non-linear chemical source term is treated without closure; and (2) they assume no shape for the PDF.However, unlike the presumed-PDF methods which take a Eulerian perspective, the full-PDF methods are commonly solved with a Lagrangian particle method such as the Monte-Carlo method. So the main disadvantages are: (1) computationally expensive; (2) potential statistical error; and (3) the most marked, hard to be incorporated into existing FVM (finite volume method)-dominating CFD codes.
Recently, two methods have been developed to solve the transported-PDF in a Eulerian framework:the direct quadrature method of moments combining with the IEM micro-mixing model (DQMOM-IEM)and the stochastic fields (SF) method [47]. Principal attractions are easily incorporated into existing CFD codes, and do not resort to the chemical source term closures. Fox [1] was the first to suggest the applications of DQMOM-IEM, and the method has found some applications thereafter [48]. Preliminary results show using DQMOM-IEM is quite encouraging, but further research is needed to understand fully the applicability range of this method. The SF method employs Eulerian stochastic fields such as a Eulerian Monte Carlo field to solve the full-PDF transport equation. This method has been applied mainly to combustion [49] and to mixing-sensitive chemical reactions very recently [48].
3.2.3 LES and turbulent mixing
Until now, all Eulerian micro-mixing models we have discussed are based on the Reynolds averaging approach. Due to the ever-increasing computer power,large eddy simulations (LES) become more and more popular. In the LES, spatial filtering is employed to treat an instantaneous scalar transport equation, however, the closure problems similar to those in the Reynolds averaging approach still exist [1, 50]. Like the two approaches used in the Reynolds averaging approach, i.e., the moment closures and the PDF methods, two similar approaches, i.e., the linear eddy model (LEM) [51] and the filtered density function(FDF) [52] were adopted in the LES. Extremely high computational requirements are needed in the LEM models. The FDF is very similar to the PDF in several ways: (1) no closure for the filtered chemical source term; and (2) a FDF transport equation similar to that for the PDF can also be derived. Likewise, the unclosed terms concerning molecular mixing in the FDF transport equation must be modeled with micro-mixing models. The Lagrangian micro-mixing models for the transported PDF, such as IEM, CD, EMST and PSP,can also be applicable to the FDF, and the Larangian particle tracking method can also be employed to solve the FDF equation [45].
3.3 Perspective on micro-mixing models
Lagrangian theoretical micro-mixing models distinguish clearly between different mechanisms of meso- and micro-mixing. However, they emphasize mainly on the contribution of small-scale mixing, and the interaction between large-scale and small-scale mixing cannot be well described. On the other hand,the PDF closure methods do not distinguish the contributions of large-scale and small-scale mixing mechanisms, and try to model the interactions between the whole scales of mixing, which is much less universally applicable and much more difficult than modeling over a small range of length scales [37]. For complex reactions, the PDF methods will be mathematically very complex. Moreover, modeling the molecular diffusion termis very complex,since a lot of requirements like boundedness, localness, linearity and independence need to be met [1].However, with relatively easy manipulation and easy incorporation into existing FVM-dominating CFD codes, the PDF methods have found wide applications,such as in combustion and precipitation.
The PDF especially the presumed-PDF model makes oversimplified assumptions, which may lead to many uncertainties or even unrealistic results. The transported-PDF method has shown some advantages over the presumed-PDF method, however, its applicability still needs to be justified. Applying PDF methods to precipitations such as BaSO4precipitation has shown that the accuracy and reliability of PDF in precipitation simulations is uncertain for now [44]. On the other hand, the models like the E-model and the IEM model are truly more theoretically based, however,oversimplified modeling and assumptions are contained therein. For instance, tmicroand/or the engulfment rate is derived based on homogeneous turbulence, which is not realistic. Also, the models used to describe species elements ranging from large-scale to finally molecular-scale are apparently oversimplified.Moreover, both theoretical models and PDF methods must deal with the molecular transfer term, which poses great challenges.
Generally, none of existing models can describe the interactions between different scales while highlighting the importance of individual processes.Clearly, more work is needed and future work may focus on the following aspects: (1) developing more sophisticated models like the PSP for closing(2) borrowing results from the studies on inhomogeneous turbulence to investigate in detail the motion and mass transfer of eddies which are on much finer scales, and to correlate the micro-mixing time or rate to the flow more accurately; (3) developing a heuristic model, which is from the perspective of CFD and can cover the whole spectrum of scales and the physical sub-processes. Concerning multiphase micro-mixing, to our best knowledge, the studies from modeling and numerical perspectives are still lacking.And multiphase micro-mixing experiments, the characterization and reliable modeling on multiphase flows with intermediate or high loadings should be addressed first.
4 CONCLUSIONS AND REMARKS
Micro-mixing experiments in single-phase vessels have been conducted extensively, and valuable data have been documented. None of existing test reactions is perfect, thus, efforts are still needed. Future work should focus on the systems with multi-impellers and special conditions such as boiling.
The introduction of dispersed phases brings new problems for the test reactions. Reported studies on two-phase micro-mixing experiments have been limited to a narrow range of conditions. Disparities between different studies widely exist. Multiphase micro-mixing experiments demand more advanced techniques, and need more in-depth and comprehensive work.
Lagrangian micro-mixing models take the well macro-mixed assumption, and the determination of tmicrois either empirical or ideal conditions based. Being coupled with CFD to describe macro-mixing is the way to overcome these shortcomings. However,combing the Lagrangian framework with the Eulerian one gives rise to new problems.
PDF models make oversimplified assumptions,which may lead to many uncertainties or even unrealistic results. The transported-PDF method has shown some advantages over the presumed-PDF method,however, its applicability still needs to be justified.The accuracy and reliability of applying PDF methods to precipitations are still uncertain.
The LEM and the FDF models are similar to the moment closures and the PDF methods in the Reynolds averaging. The LEM needs very high computational demands. Applications of FDF in chemical industry are still very limited, but it could be very promising.
Future in-depth work on micro-mixing models is needed, especially on developing a heuristic model.Modeling and simulating micro-mixing in multiphase systems are greatly dependent on the work on multiphase micro-mixing experiments, the characterization and reliable modeling on multiphase flows.
1 Fox, R.O., Computational Models for Turbulent Reacting Flows,Cambridge University Press, Cambridge (2003).
2 Xu, S., Feng, L., Wang, K., “Mixing in the production of polybutadiene rubber”, China Elastomerics, 6 (4), 49-52 (1996). (in Chinese)
3 Pohorecki, R., Baldyga, J., “New model of micromixing in chemical reactors (1) General development and application to a tubular reactor”, Ind. Eng. Chem. Fund., 22, 392-397 (1983).
4 Baldyga, J., Bourne, J.R., “A fluid-mechanical approach to turbulent mixing and chemical reaction. Part 2. Micromixing in the light of turbulence theory”, Chem. Eng. Commun., 28, 243-258 (1984).
5 Baldyga, J., Pohorecki, R., “Turbulent micromixing in chemical reactors—a review”, Chem. Eng. J., 58 (2), 183-195 (1995).
6 Baldyga, J., Bourne, J.R., Turbulent Mixing and Chemical Reactions,Wiley, New York (1999).
7 Bourne, J.R., Kozicki, F., Rys, P., “Mixing and fast chemical reaction (I) Test reactions to determine segregation”, Chem. Eng. Sci., 36(10), 1643-1648 (1981).
8 Bourne, J.R., Yu, S., “Investigation of micromixing in stirred tank reactors using parallel reactions”, Ind. Eng. Chem. Res., 33, 41-55(1994).
9 Villermaux, J., Fournier, M.C., “Potential use of a new parallel reaction systems to characterize micromixing in stirred tank”, AIChE Symp. Ser. 299, 90, 50-54 (1994).
10 Guichardon, P., Falk, L., Andrieu, M., “Experimental comparison of the iodide-iodate and the diazo coupling micromixing test reactions in stirred reactors”, Trans. IChemE, 79, 906-914 (2001).
11 Wang, Z., “Numerical simulation and experimental study of mixing and precipitation in stirred tank”, Ph.D. Thesis, Institute of Process Engineering, Chinese Academy of Sciences, Beijing, China (2005).(in Chinese)
12 Assirelli, M., Bujalski, W., Eaglesham, A., Nienow, A.W., “Intensifying micromixing in a semi-batch reactor using a rushton turbine”,Chem. Eng. Sci., 60 (8-9), 2333-2339 (2005).
13 Guichardon, P., Falk, L., Fournier, M.C., Villermaux, J., “Study of micromixing in a liquid-solid suspension in a stirred tank”, AIChE Symp. Ser. 305, 91, 123-130 (1995).
14 Barresi, A.A., “Experimental investigation of interaction between turbulent liquid flow and solid particles and its effects on fast reactions”, Chem. Eng. Sci., 52, 807-814 (1997).
15 Hofinge, J., Sharpe, R.W., Bujalski, W., Bakalis, S., Assirelli, M.,Eaglesham, A., Nienow, A.W., “Micromixing in two-phase (g-l and s-l) systems in a stirred tank”, Can. J. Chem. Eng., 89, 1029-1039(2011).
16 Barresi, A.A., “Selectivity of mixing-sensitive reactions in slurry systems”, Chem. Eng. Sci., 55, 1929-1933 (2000).
17 Gore, R.A., Crowe, C.T., “Effect of particle size on modulating turbulent intensity”, Int. J. Multiphase Flow, 15 (2), 279-285 (1989).
18 Unadkat, H., Rielly, C.D., Hargrave, G.K., Nagy, Z.K., “Application of fluorescent PIV and digital image analysis to measure turbulence properties of solid-liquid stirred suspensions”, Chem. Eng. Res. Des.,87 (4), 573-586 (2009).
19 Montante, G., Occulti, M.H., Magelli, F., Paglianti, A., “PIV measurements of mean flow and turbulence modulation in dilute solid-liquid stirred tanks”, In: 15th Int. Symp. on Appl. of Laser Techniques to Fluid Mechanics, Lisbon, Portugal (2010).
20 Zhang, Q.H., “Experimental and numerical study of macro-mixing and micro-mixing in a stirred tank”, Ph.D. Thesis, Institute of Process Engineering, Chinese Academy of Sciences, Beijing, China(2009). (in Chinese)
21 Lin, W.W., Lee, D.J., “Micromixing effects in aerated stirred tank”,Chem. Eng. Sci., 52 (21), 3837-3842 (1997).
22 Brilman, D.W.F., Antink, R., van Swaaij, W.P.M., Versteeg, G.F.,“Experimental study of the effect of bubbles, drops and particles on the product distribution for a mixing sensitive, parallel-consecutive reaction system”, Chem. Eng. Sci., 54 (13-14), 2325-2337 (1999).
23 Zhao, D., Muller-Steinhagen, H., Smith, J.M., “Micromixing in boliling and hot sparged systems—Development of a new reaction pair”, Trans. IChemE, 80, 880-886 (2002).
24 Curl, R.L., “Dispersed phase mixing (1) Theory and effects in simple reactors”, AIChE J., 9 (2), 175-181 (1963).
25 Mehta, R.V., Tarbell, J.M., “Four environment model of mixing and chemical reaction. Part I. Model development”, AIChE J., 29,320-329 (1983).
26 Villermaux, J., Devillon, J.C., “Representation de la coalescence et de la redispersion des domaines de segregation dans un fluide par un modele d’interaction phenomenologique”, In: Proc. Second Intern.Symp. on Chem. React. Eng., Amsterdam, the Netherlands, 1-13(1972).
27 Fox, R.O., Erjaee, G., Zou, Q., “Bifurcation and stability analysis of micromixing effects in the chlorite-iodide reaction”, Chem. Eng. Sci.,49, 3465-3484 (1994).
28 Pohorecki, R., Baldyga, J., “The inluence of intensity of mixing on the rate of precipitation”, In: Proc. Industrial Crystallization ′78,North-Holland, Amsterdam, 249-258 (1979).
29 Baldyga, J., Bourne, J.R., “A fluid-mechanical approach to turbulent mixing and chemical reaction. Part 3. Computational and experimental results for the new micromixing model”, Chem. Eng. Commun., 28, 259-281 (1984).
30 Baldyga, J., Bourne, J.R., “Simplification of micromixing calculations (I) Derivation and application of new model”, Chem. Eng. J.,42, 83-92 (1989).
31 Baldyga, J., Bourne, J.R., Hearn, S.J., “Interaction between chemical reactions and mixing on various scales”, Chem. Eng. Sci., 52,457-466 (1997).
32 Li, X., Chen, G.T., Chen, J.F., “Simplified framework for description of mixing with chemical reactions (1) Physical picture of micro- and macromixing”, Chin. J. Chem. Eng., 4 (4), 311-321 (1996).
33 Li, X., Chen, G.T., “Simplified framework for description of mixing with chemical reactions (2) Chemical reactions in the different mixing regions”, Chin. J. Chem. Eng., 4 (4), 322-332 (1996).
34 Baldyga, J., Podgorska, W., Pohorecki, R., “Mixing-precipitation model with application to double feed semibatch precipitation”,Chem. Eng. Sci., 50 (8), 1281-1300 (1995).
35 Akiti, O., Armenante, P.M., “Experimentally-validated micromixing-based CFD model for fed-batch stirred-tank reactors”, AIChE J.,50 (3), 566-577 (2004).
36 Phillips, R., Rohani, S., Baldyga, J., “Micromixing in a single-feed semi-batch precipitation process”, AIChE J., 45 (1), 82-92 (1999).
37 Ranade, V.V., Bourne, J.R., “Reactive mixing in agitated tanks”,Chem. Eng. Commun., 99, 33-53 (1991).
38 Toor, H.L., “Turbulent mixing of two species with and without chemical reactions”, Ind. Eng. Chem. Fundam., 8, 655-659 (1969).
39 Patterson, G.K., “Application of turbulence fundamentals to reactor modelling and scaleup”, Chem. Eng. Commun., 8, 25-52 (1981).
40 Baldyga, J., Bourne, J.R., “Comparison of the engulfment and the interaction-by-exchange-with-the-mean micromixing models”, Chem.Eng. J., 45, 25-31 (1990).
41 Marchisio, D.L., Barresi, A.A., Fox, R.O., “Simulation of turbulent precipitation in a semi-batch taylor-couette reactor using CFD”,AIChE J., 47 (3), 664-676 (2001).
42 Wang, Z., Zhang, Q.H., Yang, C., Mao, Z.S., Shen, X.Q., “Simulation of barium sulfate precipitation using CFD and FM-PDF modeling in a continuous stirred tank”, Chem. Eng. Technol., 30 (12),1642-1649 (2007).
43 Veroli, G.d., Rigopoulos, S., “Modeling of turbulent precipitation: a transported population balance-PDF method”, AIChE J., 56 (4),878-892 (2010).
44 ?ncül, A.A., Janiga, G., Thévenin, D., “Comparison of various micromixing approaches for computational fluid dynamics simulation of barium sulfate precipitation in tubular reactors”, Ind. Eng. Chem.Res., 48, 999-1007 (2009).
45 Meyer, D.W., Jenny, P., “Micromixing models for turbulent flows”, J.Comput. Phy., 228, 1275-1293 (2009).
46 Meyer, D.W., Jenny, P., “A mixing model for turbulent flows based on parameterized scalar profiles”, Phys. Fluids, 18 (3), 035105 (2006).
47 Valino, L., “A field Monte Carlo formulation for calculating the probability density function of a single scalar in a turbulent flow”,Flow Turbul. Combust., 60 (2), 157-172 (1998).
48 Akroyd, J., Smith, A.J., McGlashan, L.R., Kraft, M., “Comparison of the stochastic fields method and DQMoM-IEM as turbulent reaction closures”, Chem. Eng. Sci., 65, 5429-5441 (2010).
49 Jones, W.P., Navarro-Martinez, S., “Numerical study of n-heptane autoignition using LES-PDF methods”, Flow Turbul. Combust., 83(3), 407-423 (2009).
50 Pope, S.B., Turbulent Flows, Cambridge University Press, Cambridge (2000).
51 Kerstein, A.R., “A linear-eddy model of turbulent scalar transport and mixing”, Combust. Sci. Technol., 60 (4-6), 391-421 (1988).
52 Colucci, P.J., Jaberi, F.A., Givi, P., Pope, S.B., “Filtered density function for large eddy simulation of turbulent reacting flows”, Phys.Fluids, 10 (2), 499-515 (1998).
 Chinese Journal of Chemical Engineering2012年1期
Chinese Journal of Chemical Engineering2012年1期
- Chinese Journal of Chemical Engineering的其它文章
- Low-temperature Electrodeposition of Aluminium from Lewis Acidic 1-Allyl-3-methylimidazolium Chloroaluminate Ionic Liquids*
- In-situ Synthesis and Catalytic Properties of ZSM-5/Rectorite Composites as Propylene Boosting Additive in FluidCatalytic Cracking Process*
- Solvent Extraction of Yttrium by Task-specific Ionic Liquids Bearing Carboxylic Group*
- An Experimental Study of Liquid-Liquid Microflow Pattern Maps Accompanied with Mass Transfer*
- Liquid-Liquid-Liquid Three Phase Extraction Apparatus: Operation Strategy and Influences on Mass Transfer Efficiency*
- Micron-sized Magnetic Polymer Microspheres for Adsorption and Separation of Cr(VI) from Aqueous Solution*
