一類利普希茨非線性系統(tǒng)的全局有限時(shí)間控制
王 康 沈艷軍
(三峽大學(xué)理學(xué)院,湖北宜昌 443002)
近年來,非線性系統(tǒng)穩(wěn)定性研究成為了研究熱點(diǎn),Lyapunov穩(wěn)定性是非線性系統(tǒng)研究的重要內(nèi)容之一,學(xué)者們研究各類非線性系統(tǒng)已得出了許多好的結(jié)果,如非線性系統(tǒng)的指數(shù)穩(wěn)定等.然而,具有Lyapunov穩(wěn)定性的系統(tǒng)有時(shí)在工程上的應(yīng)用效果并不好,這就要求人們關(guān)注系統(tǒng)在有限時(shí)間內(nèi)所能達(dá)到的性能要求,非線性系統(tǒng)的有限時(shí)間控制問題也就應(yīng)運(yùn)而生[1-15].所謂有限時(shí)間控制問題是指能否在有限時(shí)間內(nèi)將系統(tǒng)控制到平衡點(diǎn).
指數(shù)穩(wěn)定是被控系統(tǒng)最快收斂速度,但此時(shí)的絕大多數(shù)閉環(huán)系統(tǒng)不可能在有限時(shí)間收斂到平衡點(diǎn).當(dāng)系統(tǒng)具有外部干擾和不確定因素影響時(shí),有限時(shí)間穩(wěn)定的系統(tǒng)往往具有更好的性能[2],因而非線性系統(tǒng)有限時(shí)間控制器的設(shè)計(jì)和穩(wěn)定性分析更為復(fù)雜.目前,研究非線性系統(tǒng)有限時(shí)間控制問題的方法主要有:文獻(xiàn)[3-4]利用齊次性理論證明齊次系統(tǒng)的有限時(shí)間穩(wěn)定及控制器的設(shè)計(jì),文獻(xiàn)[5-9]利用反步構(gòu)造 Lyapunov函數(shù)解決了非線性系統(tǒng)的有限時(shí)間控制問題,文獻(xiàn)[10-11]利用終端滑模控制方法討論非線性系統(tǒng)的有限時(shí)間控制,文獻(xiàn)[12]利用齊次性理論解決了機(jī)器人系統(tǒng)的有限時(shí)間控制問題,文獻(xiàn)[13]分別利用上述3種方法分析一類二階非線性系統(tǒng)的有限時(shí)間狀態(tài)反饋鎮(zhèn)定問題.伴隨著有限時(shí)間控制問題研究的深入,非線性系統(tǒng)的有限時(shí)間觀測器設(shè)計(jì)也得到了學(xué)者的廣泛關(guān)注[14-15].
本文討論一類Lipschitz非線性系統(tǒng)的全局有限時(shí)間控制問題,通過所構(gòu)造的一個(gè)連續(xù)非光滑的狀態(tài)反饋控制器的作用,使得該系統(tǒng)能在有限時(shí)間內(nèi)達(dá)到全局漸近穩(wěn)定,并借助 Lyapunov理論,齊次性理論及系統(tǒng)局部有限時(shí)間穩(wěn)定性理論給出了理論證明,最后,仿真結(jié)果證明了本方法的有效性.
1 預(yù)備知識(shí)
考慮如下非線性系統(tǒng):
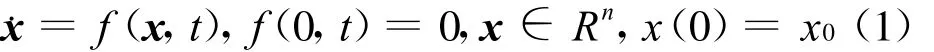
其中,f:D→Rn是連續(xù)的.

定義2[2]系統(tǒng)(1)的零解如果是Lyapunov穩(wěn)定和有限時(shí)間收斂的,則它是有限時(shí)間穩(wěn)定的.如果U=D=Rn,則它是全局有限時(shí)間穩(wěn)定的.
定義3[9](齊次函數(shù)) 假設(shè)(r1,…,rn)∈Rn, ri>0,i=1,2,…,n,V:Rn→R為連續(xù)函數(shù)V被稱為相對(duì)于(r1,…,rn)具有齊次自由度σ>0的函數(shù),如果對(duì)?ε>0,?ξ∈Rn,使得
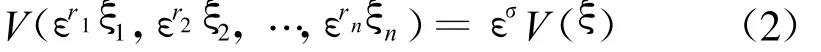
成立.
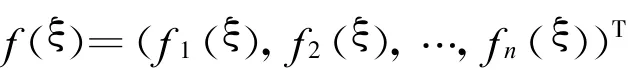
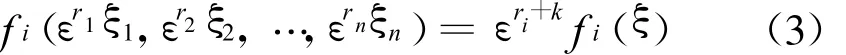
成立.
引理1[9]假設(shè)系統(tǒng)(1)相對(duì)于(r1,…,rn)具有齊次自由度k,則系統(tǒng)(1)的平衡點(diǎn)是有限時(shí)間穩(wěn)定的,當(dāng)且僅當(dāng)系統(tǒng)(1)的原點(diǎn)是漸近穩(wěn)定的平衡點(diǎn)且齊次自由度k>0.
引理2[9]假設(shè)V1和V2是在Rn連續(xù)實(shí)函數(shù),分別相對(duì)于(r1,…,rn)具有齊次自由度l1,l2(均大于0),V1為正定的,則有,對(duì)每個(gè)x∈Rn有下式
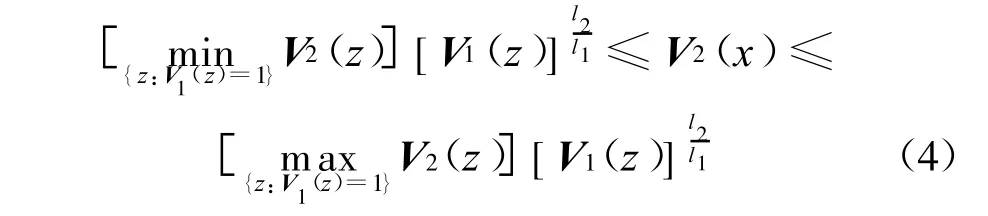
成立.
引理3[14]假設(shè)系統(tǒng)存在一個(gè)定義在原點(diǎn)的某個(gè)領(lǐng)域U∈Rn內(nèi)的Lyapunov函數(shù)V(x)滿足
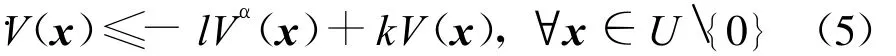
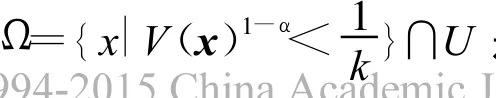
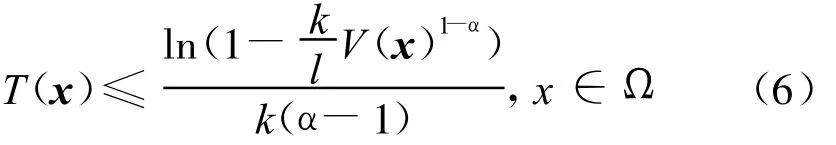
引理4 考慮以下系統(tǒng)

這里,x∈Rn是系統(tǒng)狀態(tài),hi:Rn→R是連續(xù)函數(shù)(i=1,2,…,n),若系統(tǒng)(7)是全局漸近穩(wěn)定且原點(diǎn)在某鄰域內(nèi)是有限時(shí)間穩(wěn)定的,則系統(tǒng)(7)的原點(diǎn)是全局有限時(shí)間穩(wěn)定的.
引理5[16]令c,d為正實(shí)數(shù),γ(x,y)>0為一實(shí)值函數(shù),則有下式成立:
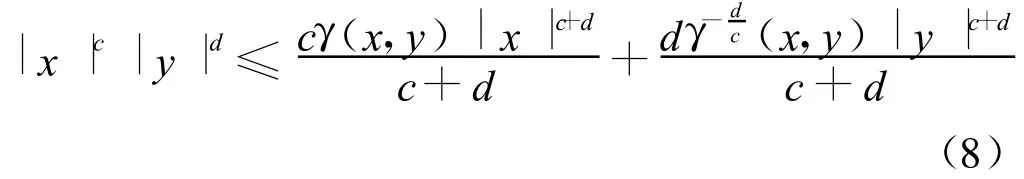
符號(hào)說明:
(1)signx為x的符號(hào)函數(shù),其定義:當(dāng)x>0時(shí), signx=1;當(dāng)x<0時(shí),signx=-1;當(dāng)x=0時(shí),signx =0.
(2)λmax(P),λmin(P)分別表示矩陣P的最大,最小特征值.
2 主要結(jié)果
考慮以下Lipschitz非線性系統(tǒng)
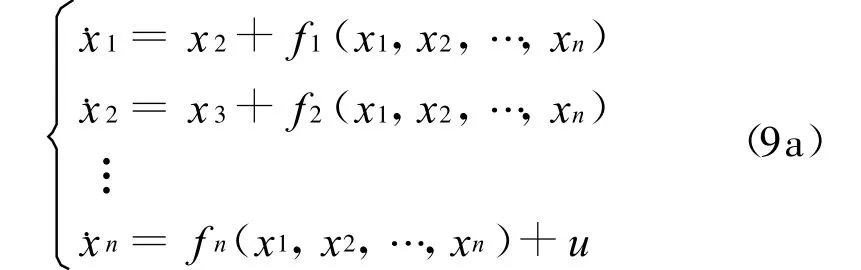
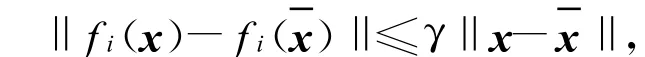
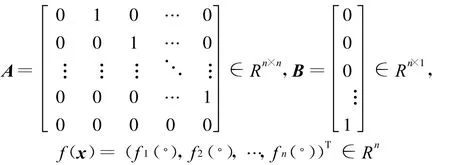
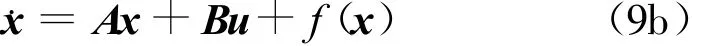
所討論系統(tǒng)的全局有限時(shí)間控制問題是指系統(tǒng)(9)在形如以下狀態(tài)反饋控制器(10)
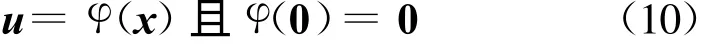
的作用下,其閉環(huán)系統(tǒng)
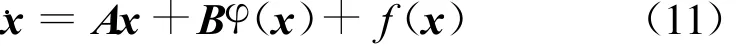
是全局有限時(shí)間穩(wěn)定的.此時(shí)控制器(10)稱為系統(tǒng)(9)的一個(gè)有限時(shí)間狀態(tài)反饋控制器.
注1:文獻(xiàn)[13]考慮了一類參數(shù)與狀態(tài)不確定性非線性系統(tǒng)的有限時(shí)間控制問題,其非線項(xiàng) fi(?)具有下三角結(jié)構(gòu),而本文考慮的非線性項(xiàng) fi(?)與所有狀態(tài)變量均有關(guān),從而更具廣泛性.
下面給出解決系統(tǒng)(9)的全局有限時(shí)間控制問題的主要定理.
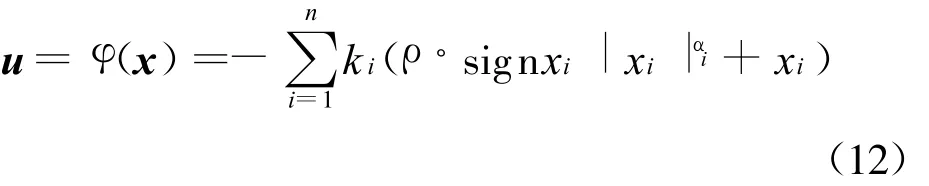
的作用下可實(shí)現(xiàn)閉環(huán)系統(tǒng)(11)是全局有限時(shí)間穩(wěn)定的,其中控制器增益ki滿足(k1,k2,…,kn)=BTQ,這里Q滿足Riccati方程:
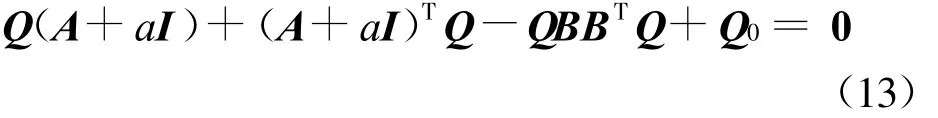
式中,a>0為適當(dāng)標(biāo)量,Q0為適當(dāng)?shù)膶?duì)稱正定矩陣, ρ,αi為控制器參數(shù)且滿足
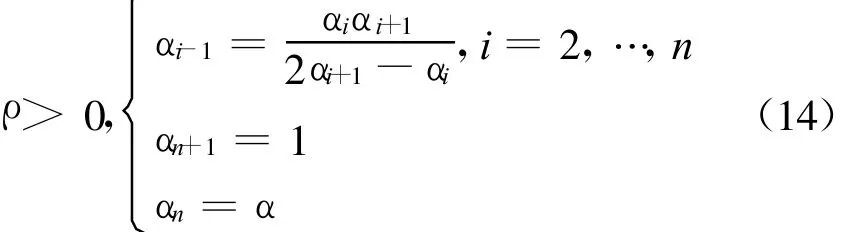
證明步驟分兩步:步驟1,用 Lyapunov直接方法,證明系統(tǒng)(11)存在一個(gè)正定且徑向無界V∈Rn,其且沿閉環(huán)系統(tǒng)(11)軌跡的微分在Pr=Rn-υQ(r)上是負(fù)定的;步驟2,證明閉環(huán)系統(tǒng)(11)在υQ(2r)上是有限時(shí)間穩(wěn)定(FTS)的.由于˙V在Pr上負(fù)定且在υQ(2r)上是FTS的,意味著系統(tǒng)(11)是全局漸近穩(wěn)定和局部FTS的,再利用引理4可完成證明.
步驟1:令系統(tǒng)(11)的正定Lypunov函數(shù)

由于控制器增益ki滿足(k1,k2,…,kn)=BTQ,則控制(12)可等價(jià)為
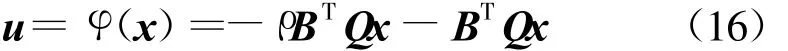
其中,x={signx1|x1|α1,signx2|x2|α2,…,signxn?|xn|αn}.
此時(shí),上式沿閉環(huán)系統(tǒng)(11)軌跡的微分為
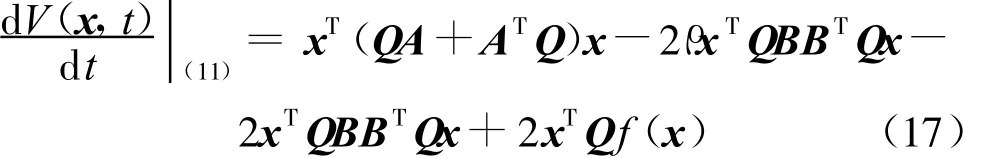
由條件(13)知:QA+ATQ+2aQ-2QBBTQ>0,將其代入式(17)可得
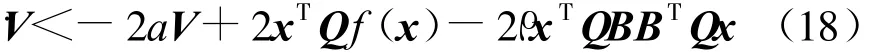
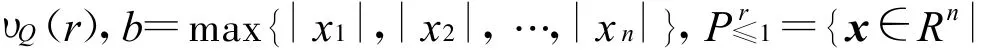
當(dāng)x∈Pr≤1時(shí),有|xi|αi≤1,i=1,2,…,n,于是有
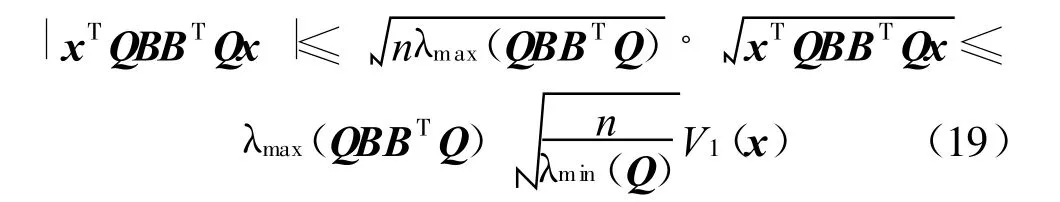
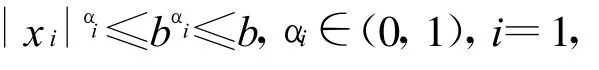
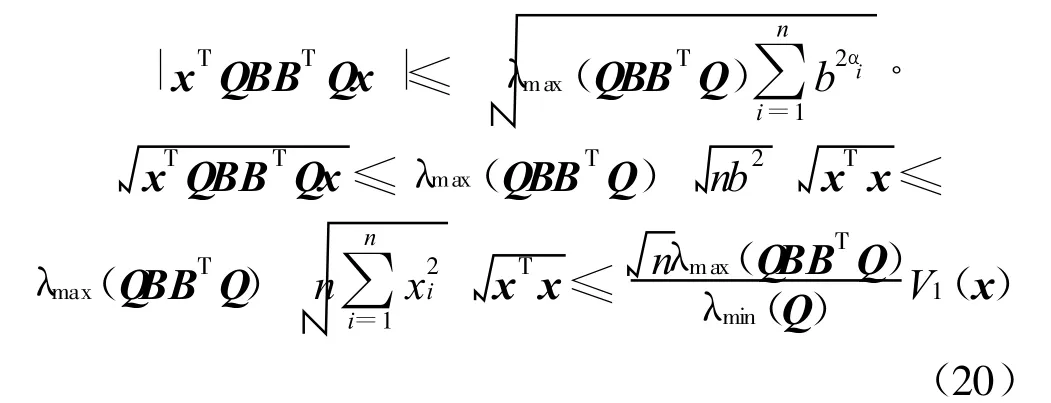
故存在
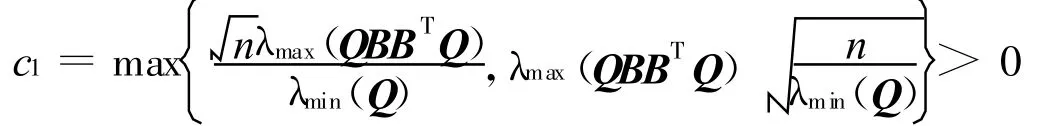
使得
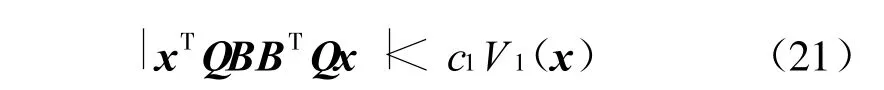
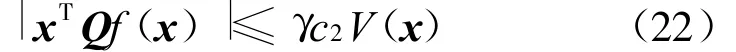
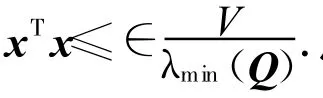
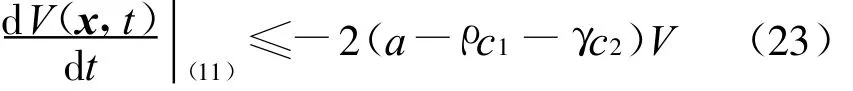

其中g(shù)(a,ρ,γ)=max{-2a+ρ c1+γ c2,-2},則有
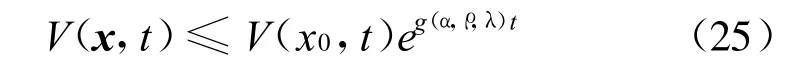
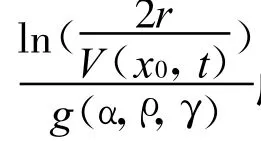
步驟2:考慮正定連續(xù)的Lyapunov函數(shù)
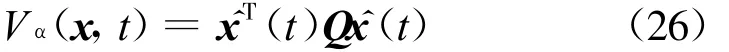
考慮以下系統(tǒng)

即
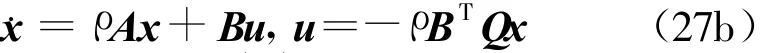
且有
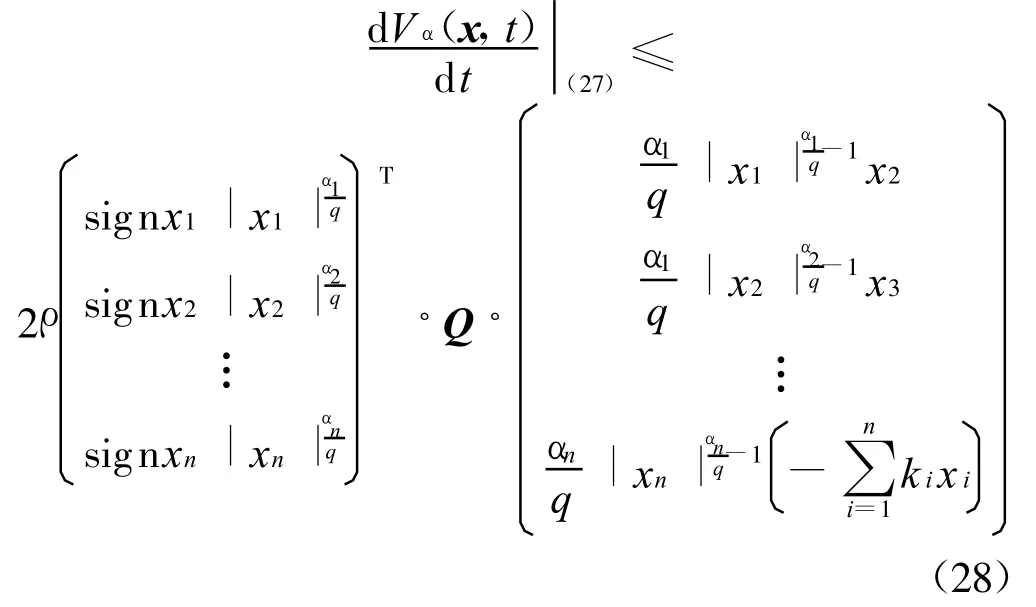
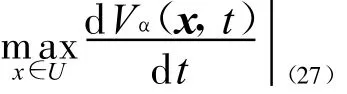
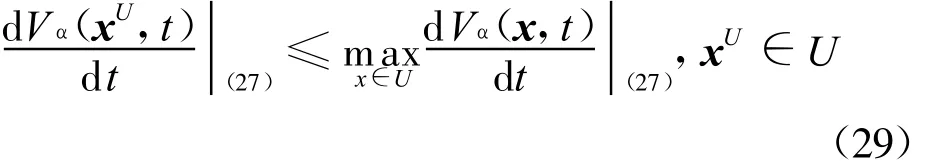
由Vα(x,t)的齊次性及引理2可知
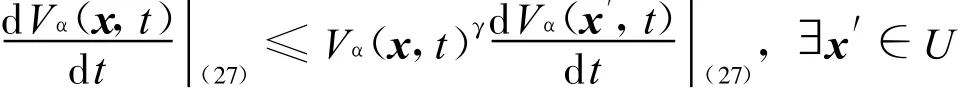
.另一方面,
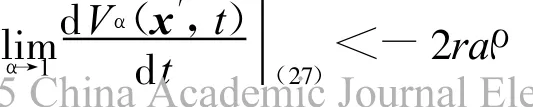
故存在ε2∈(0,1)使得對(duì)每個(gè)α∈(1-ε2,1)有
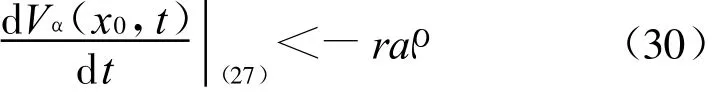
于是對(duì)?x∈υQ(2r),存在ε2∈(0,1)使得對(duì)每個(gè)α∈(1-ε2,1)有
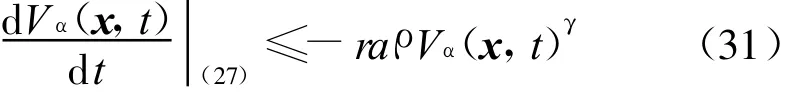
基于上述分析,可得正定Lyapunov函數(shù)Vα(x, t)沿閉環(huán)系統(tǒng)(11)軌跡的微分為

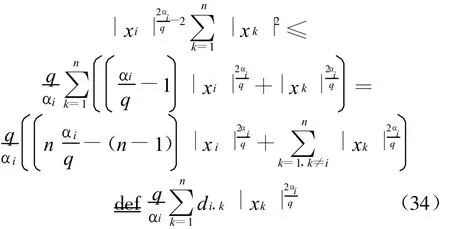
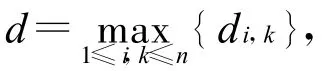

同理可得
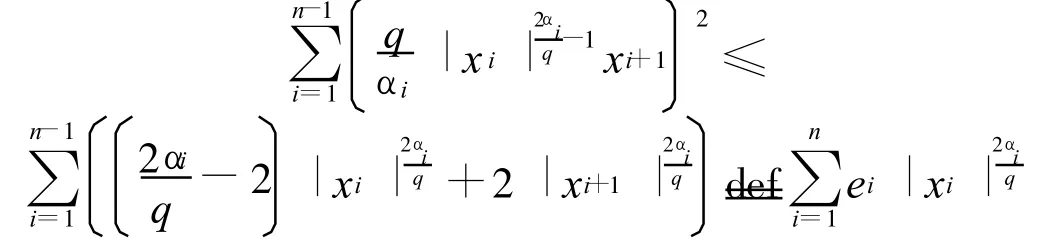
其中,ei>0,令

現(xiàn)要證明^xTQBBTQx的值不小于0,利用Tube引理,知道υQ(2r)是緊集,定義函數(shù)
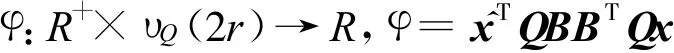
則φ是連續(xù)的.
從而有

因此,令
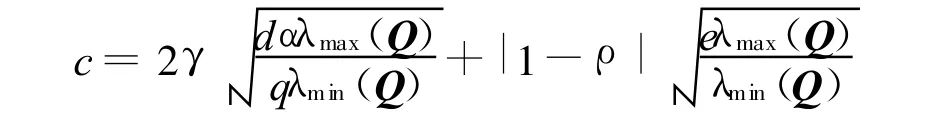
則有
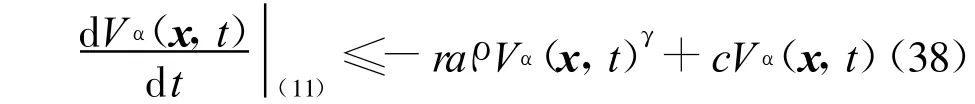
進(jìn)而,由引理3和式(38)可得一個(gè)包含原點(diǎn)的吸引域Ω,且有υQ(2r)?Ω,其中
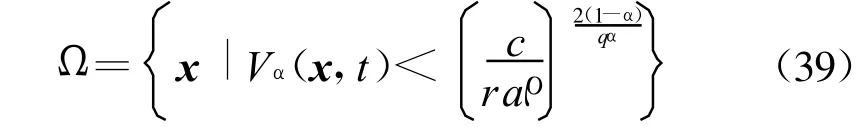
且設(shè)定時(shí)間
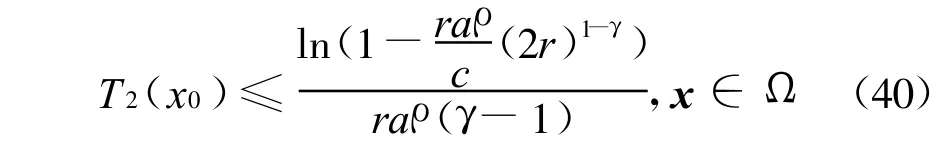
注2:由定理1,可按以下步驟設(shè)計(jì)系統(tǒng)的全局有限時(shí)間控制器(12):
(1)選定參數(shù)α,Q0,通過求解Riccati方程(13)得到Q;
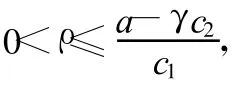
(3)設(shè)定控制器參數(shù)αi且滿足條件(14);
(4)設(shè)計(jì)形如(12)的有限時(shí)間控制器.
注3:考慮系統(tǒng)
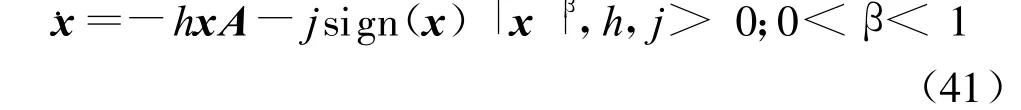
分析其解的情況,當(dāng)x遠(yuǎn)離平衡點(diǎn)原點(diǎn)時(shí),系統(tǒng)(41)可約寫為˙x=-hx,此時(shí)系統(tǒng)是指數(shù)收斂到原點(diǎn)的,當(dāng)x非常接近含原點(diǎn)的鄰域時(shí),系統(tǒng)(41)可約寫為˙x=-jsign(x)|x|β,此時(shí)系統(tǒng)是有限時(shí)間穩(wěn)定的,詳見參考文獻(xiàn)[12].
注4:從定理1的證明中不難得出,當(dāng)α=1時(shí),控制器(42)是控制器(12)的極限形式,且在其作用下能確保閉環(huán)系統(tǒng)(11)是全局漸近穩(wěn)定的:
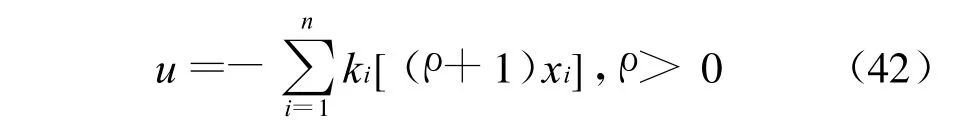
3 數(shù)值實(shí)驗(yàn)
考慮以下系統(tǒng)
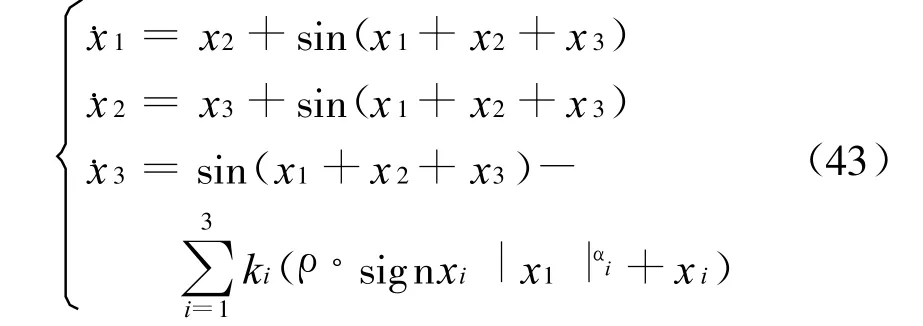


則可得有限時(shí)間控制器的增益k1=9.247 9,k2= 12.8343,k3=6.173 8,設(shè)定控制器參數(shù)為ρ=0.3, α=0.8,則可得系統(tǒng)狀態(tài)軌跡如圖1所示.
當(dāng)設(shè)定控制器(12)中的參數(shù)ρ=0.3,α=1,此時(shí)的控制器是控制器(12)的極限形式,它將不再是有限時(shí)間控制器,只是一般狀態(tài)反饋控制器,所得系統(tǒng)狀態(tài)軌跡如圖2所示.
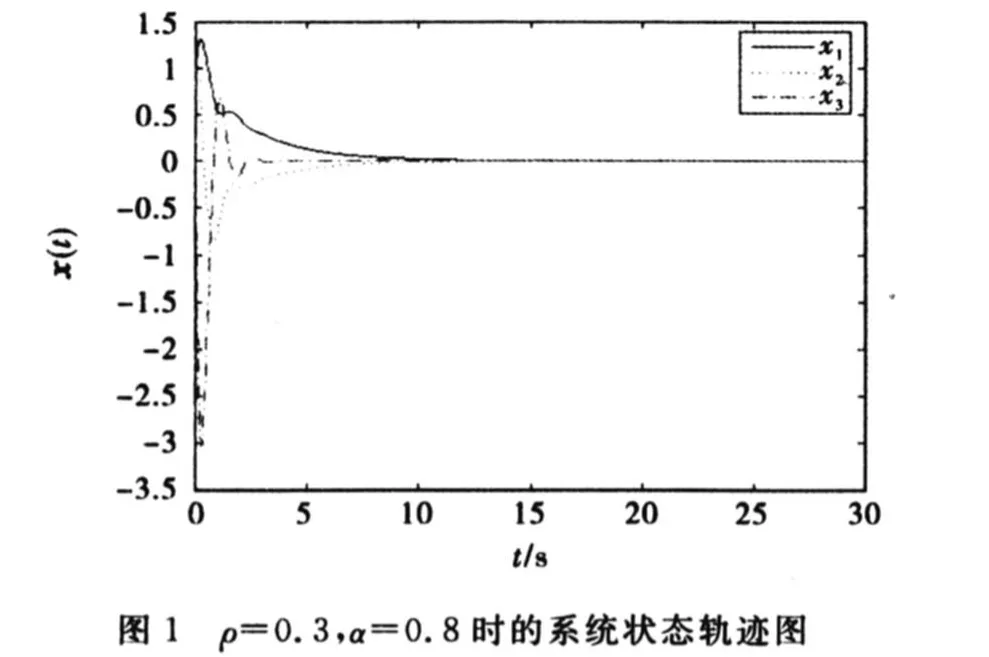
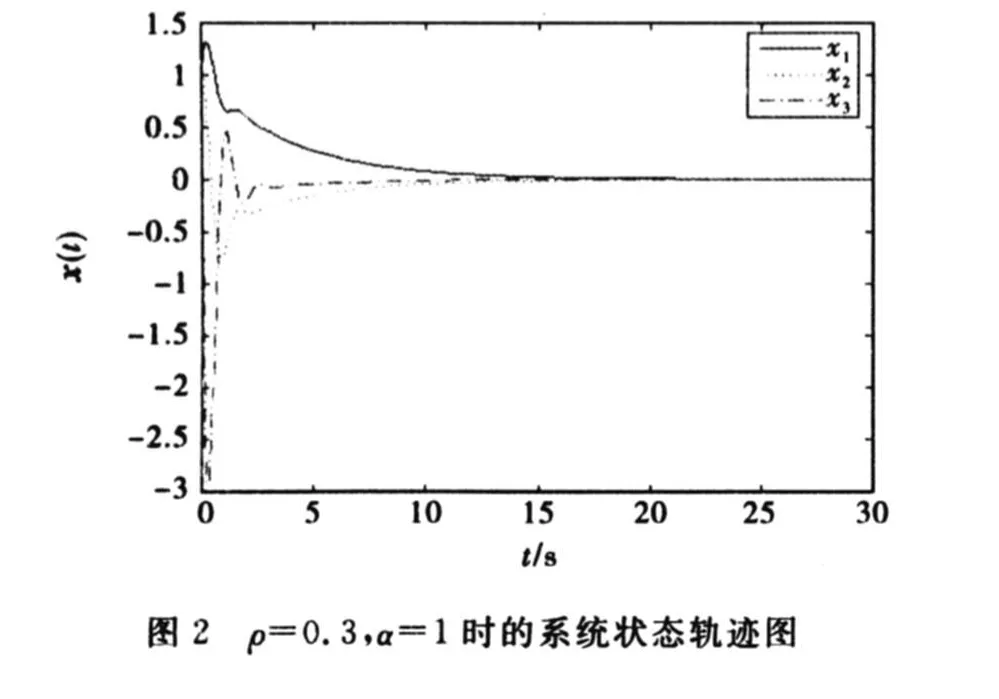
由仿真實(shí)驗(yàn)可知,圖1是系統(tǒng)(40)在有限時(shí)間控制器(12)作用下T=12s內(nèi)就達(dá)到平衡點(diǎn).圖2是系統(tǒng)(40)在控制器(39)作用下T=20 s才被控制到平衡點(diǎn).從而有力地說明了有限時(shí)間控制器比一般的狀態(tài)反饋控制器具有更優(yōu)的控制性能.
4 結(jié) 語
本文討論了一類Lipschitz非線性系統(tǒng)的全局有限時(shí)間控制問題,設(shè)計(jì)了一個(gè)有限時(shí)間狀態(tài)反饋控制器,通過Lyapunov理論,齊次系統(tǒng)理論和局部有限時(shí)間穩(wěn)定性理論證明在其作用下的閉環(huán)系統(tǒng)是全局有限時(shí)間穩(wěn)定的,并通過求解Riccati方程得到控制器增益,最后,通過實(shí)例仿真證明了本方法的正確性.
[1] Ryan E P.Finite-time Stabilization of Uncertain Nonlinear Planar Systems[J].Dyn.Control,1,1991:83-94.
[2] Bhat S P,Bernstein D S.Continuous Finite-time Stabilization of the Translational and Rotational Double Integrators[J].IEEE T rans.Autom.Control,1998,43 (5):678-682.
[3] Bhat S P,Bernstein D S.Finite-time Stability of Continuous Autonomous Systems[J].SIAM J.Control Optim,2000,38(3):751-766.
[4] Bhat S P,Bernstein D S.Geometric Homogeneity with Applications to Finite-time Stability[J].M ath.Control Signals Syst.,2005,17:101-127.
[5] Hong Y.Finite-time Stabilization and Stabilizability of a Class of Controllable Systems[J].Syst.Control Lett., 2002,46:231-236.
[6] Huang X,Lin W,Yang B.Global Finite-time Stabilization of a Class of Uncertain Nonlinear Systems[J].Automaica,2005,41:881-888.
[7] Hong Y,Jiang Z.Finite-time Stabilization of Non-linear Systems with Parametric and Dynamic Uncer-tainties [J].IEEE Trans,Automat,Control,2006,51(12): 1950-1956.
[8] 洪奕光,王劍魁.一類非線性系統(tǒng)的非光滑有限時(shí)間鎮(zhèn)定[J].中國科學(xué)E輯,2005,35(6):663-672.
[9] Hong Y,Wang J,Cheng D.Adaptive Finite-time Control of a Class of Uncertain Nonlinear Systems[J].IEEE Trans.Autom.Control,2006,51(5):858-862.
[10]Wu Y Q,Yu X H,Man Z H.Terminal Sliding Mode Control Design forUncertain Dynamic Systems[J]. Syst.Control Lett.,1998,34(5):281-288.
[11] Feng Y,Yu X H,Man Z H.Nonsingular Terminal Sliding Mode Control of Rigid Manipulators[J].Automatic,2002,38(12):2159-2167.
[12]Hong Y,Xu Y,Huang J.Finite-time Control for Robot Manipulators[J].Syst.Control Lett.,2002,46:243-253.
[13]李世華,丁世宏,田玉平.一類二階非線性系統(tǒng)的有限時(shí)間狀態(tài)反饋鎮(zhèn)定方法[J].自動(dòng)化學(xué)報(bào),2007,33(1): 101-104.
[14]Shen Y,Xia X.Semi-global Finite-time Observers for Nonlinear Systems[J].Automatica,2008,44:3152-3156.
[15]Shen Y,Huang Y.Uniformly Observable and Globally Lipschitzian Nonlinear Systems Admit Global Finitetime Observers[J].IEEE Trans,Auto mat,Control, 2009,54(11):2621-2625.
[16]Qian C,Lin W.Non-Lipschitz Continuous Stabilizer for Nonlinear Systems with Uncontrollable Unstable Linearization[J].Syst.Control Lett.,2001,42:185-200.

