Extremalθ-Graphs with Respect to Hosoya Index andM errif ield-S immons Index inΘ(n,g)
(College ofM athematics and Statistics,South-CentralU niversity for N ationalities,W uhan 430074,China)
1 Introduction
A ll graphs considered in this paper are finite,undirected and simple.L etG=(V,E)be a graph onnvertices.Two edges ofGare said to be independent if they are not adjacent inG.Akmatching ofGis a set ofkmutually independent edges.Denote byZ(G,k)the number ofkmatchings ofG.For convenience,we regard the empty edge set as a matching.ThenZ(G,0)=1 for any graphG.The Hosoya index,denoted byZ(G),isdefinedtobethetotal number of matchings,namely,
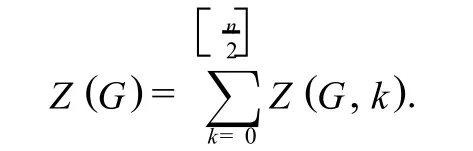
Two vertices ofGare said to be independent if they are not adjacent inG.A n independentk-set is a set ofkvertices,no two of which are adjacent.Denote byi(G,k)the number ofk-independent sets ofG.It follow s directly from definition that? is an independent set.Theni(G,0)=1 for any graphG.The M errifield-Simmons index,denoted byi(G),is defined to be the total number of independent sets ofG,that is,i(G)=
TheHosoyaindexwasintroducedby Hosoya[1]in 1971,and it turned out to be applicable to several questions of molecular chem istry.For example,the connections w ith physico-chem ical properties such as boiling point,entropy or heat of vaporization are well studied.Sim ilar connections are known for theM errifield-Simmons index,that was introduced by M errifield and Simmons[2]in 1989.For detailed information on the chem ical applications,we refer to Ref[1],[3],[4]and the references therein.
Several papers deal w ith the characterization of the extremal graphs w ith respect to these two indices in several given graph classes.U sually,trees,unicyclicgraphsandcertainstructures involving pentagonal and hexagonal cycles are of major interest Ref[5],[6].
θ-graphs are obtained by subdividing the edges of the multigraph consisting of 3 parallel edges,and they are denoted byθ(r,s,t)(see Fig.1),wherer≤s≤t.L etΘ(n,g)be set ofθ-graphsw ith given girthgand ordern,that is,Θ(n,g)={θ(r,s,t):r+s+2=g,r+s+t+2=n,r≤s≤t}.In Ref[7],Ramezani F,et al.have shown that anyθgraphGis determ inedbythespectrum(the multiset of eigenvalues)except possibly when it contains a unique 4-cycle.Tan Land Zhu Z[8]investigated the extremalθ-graphs w ith respect to Hosoya index and M errifield-Simmons index.In this paper,the extremalθ-graphs inΘ(n,g)w ith respect to Hosoya index and M errifield-Simmons index is characterized.
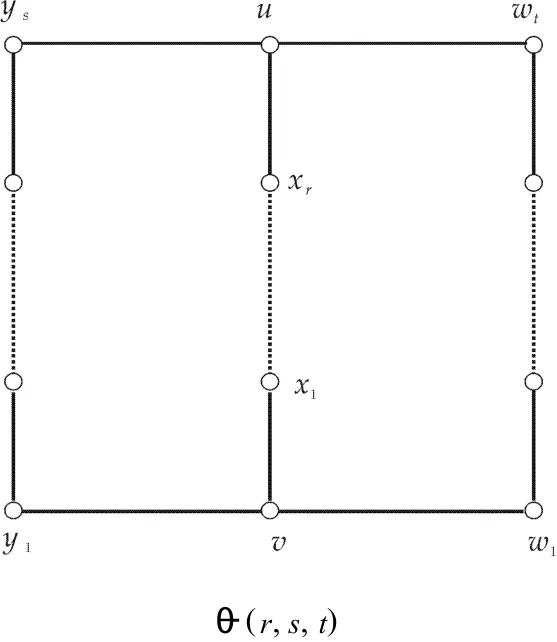
圖1 θ-圖Fig.1 θ-graph
In order to present our results,we introduce somenotationsandterm inologies.Forother undefined notation we refer to Bollobás[9].IfW?V(G),we denote byG—Wthe subgraph ofGobtained by deleting the vertices ofWand the edges incident w ith them.Sim ilarly,ifE?E(G),we denote byG-Ethe subgraph ofGobtained by deleting the edges ofE.IfW={v}andE={xy},we w riteG-vandG-xyinstead ofG-{v}andG-{xy},respectively.W e denote byPn,Cnthe path,the cycle onnvertices,respectively.L etN(v)={u|uv∈E(G)},N[v]=N(v)∪{v}.
Denote byFnthenth Fibonacci number.Recall thatFn=Fn-1+Fn-2w ith initial conditionsF0=1 andF1=1.Thenz(Pn)=Fn,i(Pn)=Fn+1.Note thatFn+m=FnFm+Fn-1Fm-1.For convenience,we letFn=0 forn<0.
The follow ing results w ill play a role key in the proof of our main results.
Lemma 1[3]L etG=(V,E)be a graph.
(i)Ifuv∈E(G),thenz(G)=z(G-uv)+z(G-{u,v});
(ii)Ifv∈V(G),thenz(G)=z(G-v)+
(iii)IfG1,G2,…,Gtare the components of the graphG,thenz(G)=
Lemma 2[3]L etG=(V,E)be a graph.
(i)Ifuv∈E(G),theni(G)=i(G-uv)-i(G-{N[u]∪N[v]});
(ii)Ifv∈V(G),theni(G)=i(G-v)+i(GN[v]);
(iii)IfG1,G2,…,Gtare the components of the graphG,theni(G)=
2 Extremal graphs with respect to the Hosoya index inΘ(n,g)
W e first consider the extremal graphs w ith respect to the Hosoya index inΘ(n,g).
Lemma 3[8,10]L etθ(r,s,t)be the graph in Fig 1,
(i)Ifr=0,thenz(θ(0,s,t))=Fs+t+2+Fs+t+
FsFt;
(ii)Ifr>0,thenz(θ(r,s,t))=FrFs+t+2+FrFs+t+2Fr-1Fs+t+1+Fr-2FsFt.
Corollary 1(i)z(θ(0,g-2,n-g))=Fn+Fn-2+Fg-2Fn-g;
(ii)Ifr>0 andθ(r,s,t)∈Θ(n,g),then z(θ(r,s,t))=FrFn-r+FrFn-r-2+2Fr-1Fn-r-1+Fr-2Fg-r-2Fn-g.
L etθ(r,s,t)∈Θ(n,g),ifg=3,thenθ(r,s,t)≌θ(0,g-2,n-g);ifg=4,θ(r,s,t)≌θ(0,g-2,n-g)orθ(r,s,t)≌θ(1,g-3,n-g).By L emma 3,we have
z(θ(0,2,n-4))=Fn+Fn-2+2Fn-4;z(θ(1,1,n-4))=Fn+Fn-2+2Fn-3.
Obviously,z(θ(0,2,n-4))>z(θ(1,1,n-4)).Hence,letg≥5 in the next of this section.
Lemma 4L etθ(0,g-2,n-g),θ(r,s,t)∈Θ(n,g),thenz(θ(0,g-2,n-g))≥z(θ(r,s,t)).The equality holds if and only ifθ(r,s,t)≌θ(0,g-2,n-g).
ProofNote thatFn=FrFn-r+Fr-1Fn-r-1and Fn-2=FrFn-r-2+Fr-1Fn-r-3.Ifr=0,thenθ(r,s,t)≌θ(0,g-2,n-g).Ifr≥1,by Corollary 1,we have:
z(θ(0,g-2,n-g))-z(θ(r,s,t))=
FrFn-r+Fr-1Fn-r-1+FrFn-r-2+Fr-1Fn-r-3+
Fg-2Fn-g-[FrFn-r+FrFn-r-2+2Fr-1Fn-r-1+
Fr-2Fg-r-2Fn-g]=Fg-2Fn-g+Fr+1(Fn-r-3-
Fn-r-1)-Fr-2Fg-r-2Fn-g=Fr-1Fg-r-3Fn-g-2.
Sinceg=r+s+2≥2r+2≥r+3 andθ(0,g-2,ng)∈Θ(n,g),thenn≥2g-2,andn-g-2≥g-4>0.SoFr-1Fg-r-3Fn-g-2>0.Hencez(θ(0,g-2,n-g))>z(θ(r,s,t)).
This complete the proof.
Lemma 5θ(1,g-3,n-g),θ(r,s,t)∈Θ(n,g),thenz(θ(r,s,t))≥z(θ(1,g-3,n-g)).
The equality holds if and only ifθ(r,s,t)≌θ(1,g-3,n-g).
ProofBy Corollary 1(ii),
z(θ(1,g-3,n-g))=Fn+Fn-1.
Ifr=0,thenθ(r,s,t)≌θ(0,g-2,n-g).By L emma 4,it hasz(θ(r,s,t))>z(θ(1,g-3,ng)).
Ifr=1,thenθ(r,s,t)≌θ(1,g-3,n-g).
Ifr≥2,z(θ(r,s,t))-z(θ(1,g-3,n-g))=FrFn-r+FrFn-r-2+2Fr-1Fn-r-1+Fr-2Fg-r-2Fn-g-[FrFn-r+Fr-1Fn-r-1+FrFn-r-1+Fr-2Fn-r-2]=Fr-2Fg-r-2Fn-g-FrFn-r-3+Fr-1Fn-r-3=Fr-2Fg-r-4Fn-g-2.
Sinceg=r+s+2≥2r+2≥r+4 andn-g≥g-3,thenn-g-2≥g-5,thenFr-2Fg-r-4Fn-g-2>0.Hencez(θ(r,s,t))>z(θ(1,g-3,n-g)).
This complete the proof.
Bytheabovediscussion,wehavethe follow ing Theorem 1.
Theorem 1For anyθ(r,s,t)∈Θ(n,g),Fn+Fn-2+Fg-2Fn-g≥z(θ(r,s,t))≥Fn+Fn-1,w ith the first equality holds if and only ifθ(r,s,t)≌θ(0,g-2,n-g),and the last equality holds if and only ifθ(r,s,t)≌θ(1,g-3,n-g).
3 Extremal graphs with respect to the M errif ield-S immons index in Θ(n,g)
Nowwestudytheextremal graphs w ith respect to the M errifield-Simmons index inΘ(n,g).
Lemma 6[8]L etθ(r,s,t)be the graph in Fig.1,
(i)Ifr=0,theni(θ(0,s,t))=Fs+t+3-Fs+t-1-Fs-1Ft-1;
(ii)Ifr>0,theni(θ(r,s,t))=Fr+1Fs+1Ft+1+2FrFsFt+Fr-1Fs-1Ft-1.
Corollary 2(i)i(θ(0,g-2,n-g))=Fn+Fn-2-Fg-3Fn-g-1;
(ii)i(θ(1,g-3,n-g))=2Fn-1+Fg-4Fn-g-1.
L etθ(r,s,t)∈Θ(n,g),ifg=3,thenθ(r,s,t)≌θ(0,g-2,n-g);ifg=4,θ(r,s,t)≌θ(0,g-2,n-g)orθ(r,s,t)≌θ(1,g-3,n-g).By L emma 6,we have:
i(θ(0,2,n-4))=Fn+Fn-2-Fn-5;i(θ(1,1,n-4))=2Fn-1+Fn-5.
Obviously,i(θ(1,1,n-4))>i(θ(0,2,n-4)).Hence,letg≥5 in the next of this section.
Lemma 7Ifθ(0,g-2,n-g),θ(r,s,t)∈Θ(n,g),theni(θ(r,s,t))≥i(θ(0,g-2,n-g)).The equality holds if and only ifθ(r,s,t)≌θ(0,g-2,n-g).
ProofIfr=0,thenθ(r,s,t)≌θ(0,g-2,ng).
Ifr=1,θ(r,s,t)≌θ(1,g-3,n-g).
i(θ(1,g-3,n-g))-i(θ(0,g-2,n-g))=2Fn-1+Fg-4Fn-g-1-[Fn+Fn-2-Fg-3Fn-g-1]=Fg-2Fn-g-1-Fn-4=Fg-2Fn-g-1-Fg-2Fn-g-2-Fg-3Fn-g-3=Fg-2Fn-g-3-Fg-3Fn-g-3=Fg-4Fn-g-3,
sincen-g≥g-3,thenn-g-2≥g-5≥0,thenFg-4Fn-g-3>0.Hencei(θ(1,g-3,n-g))>i(θ(0,g-2,n-g)).
Ifr=2,θ(r,s,t)≌θ(2,g-4,n-g).
i(θ(2,g-4,n-g))-i(θ(0,g-2,n-g))=3Fn-2+Fn-4-[Fn+Fn-2-Fg-3Fn-g-1]=
Fg-3Fn-g-1-Fn-5=
Fg-3Fn-g-1-Fg-3Fn-g-2-Fg-4Fn-g-3=
Fg-5Fn-g-3,
2Fr-1+Fg-4Fn-g-1-[Fr+1Fs+1Ft+1+2FrFsFt+Fr-1Fs-1Ft-1]=2Fr+s+t+1+Fr+s-2Ft-1-
[Fr+1Fs+1Ft+1+2FrFsFt+Fr-1Fs-1Ft-1]=2FrFs-1Ft+2FrFsFt-1+2Fr-1FsFt+
2Fr-1Fs-1Ft-1+Fr-2Fs-2Ft-1-Fr+1Fs+1Ft+1=Fr-2Fs-2Ft-3.
Sincer≤s≤t,thenFr-2Fs-2Ft-3>0.Hencei(θ(1,g-3,n-g))>i(θ(r,s,t)).
Bytheabovediscussion,wehavethe follow ing Theorem 2.
Theorem 2For anyθ(r,s,t)∈Θ(n,g),2Fn-1+Fg-4Fn-g-1≥i(θ(r,s,t))≥Fn+Fn-2-Fg-3Fn-g-1,w ith the first equality holds if and only ifθ(r,s,t)≌θ(1,g-3,n-g),and the last equality holds if and only ifθ(r,s,t)≌θ(0,g-2,n-g).
sincen-g≥g-3,thenn-g-2≥g-5≥0,thenFg-5Fn-g-3>0.Hencei(θ(2,g-4,n-g))>i(θ(0,g-2,n-g)).
Ifr≥3,by L emma 6 and Corollary 2,i(θ(r,s,t))-i(θ(0,g-2,n-g))=
Fr+1Fs+1Ft+1+2FrFsFt+Fr-1Fs-1Ft-1-
[Fr+s+t+2+Fr+s+t-Fg-3Fn-g-1]=
Fr+1Fs+1Ft+1+2FrFsFt+Fr-1Fs-1Ft-1-
[FrFs+t+2+Fr-1Fs+t+1+FrFs+t+Fr-1Fs+t-1-Fg-3Fn-g-1]=
Fr-1Fs-1Ft-3+Fr-1Fs-1Ft-1+Fr-1Fs-2Ft-1-Fr-1FsFt-1=Fr-1Fs-1Ft-3.
Sincer≤s≤t,thenFr-1Fs-1Ft-3>0.Hencei(θ(r,s,t))>i(θ(0,g-2,n-g)).
This complete the proof.
Lemma 8Ifθ(1,g-3,n-g),θ(r,s,t)∈Θ(n,g),theni(θ(1,g-3,n-g))≥i(θ(r,s,t)).The equality holds if and only ifθ(r,s,t)≌θ(1,g-3,n-g).
ProofIfr=0,thenθ(r,s,t)≌θ(0,g-2,ng).By L emma 7,it hasi(θ(1,g-3,n-g))>i(θ(r,s,t)).
Ifr=1,thenθ(r,s,t)≌θ(1,g-3,n-g).
Ifr=2,θ(r,s,t)≌θ(2,g-4,n-g).
i(θ(1,g-3,n-g))-i(θ(2,g-4,n-g))=2Fn-1+Fg-4Fn-g-1-[3Fn-2+Fn-4]=Fg-4Fn-g-1-
Fn-6=Fg-4Fn-g-1-Fg-4Fn-g-2-Fg-5Fn-g-3=
Fg-4Fn-g-3-Fg-5Fn-g-3=Fg-6Fn-g-3.
sinceg=r+s+2≥2r+2≥6 andn-g≥g-3,thenn-g-2≥g-6≥0,soFg-6Fn-g-3>0.Hencei(θ(1,g-3,n-g))>i(θ(2,g-4,n-g)).
Ifr≥3,by L emma 6 and Corollary 2,i(θ(1,g-3,n-g))-i(θ(r,s,t))=
[1] Hosoya H.Topological index,a new ly proposed quantity characterizingthetopological nature of structural isomers of saturated hydrocarbons[J].Bull Chem Soc Jpn,1971,44:2332-2339.
[2] M errifield R E,S immons H E.Topological methods in chem istry[M].N ew York:W iley,1989.
[3] Gutman I,Polansky O E.M athematical concepts in organic chem istry[M].Berlin:Springer-V erlag,1986.
[4] L i X,L i Z,W ang L.The inverse problem s for some topological indices in combinatorial chem istry[J].J Comput Biol,2003,10:47-55.
[5] L i S,Zhu Z.The number of independent sets in unicyclic graphs w ith a given diameter[J].D iscrete ApplM ath,2009,157:1387-1395.
[6] Zhu Z,L i S,Tan L.T ricyclic graphs w ith max imum M errifield-S immons index[J].D iscrete Appl M ath,2010,158:204-212.
[7] Ramezani F,Broojerdian N,Tayfeh-RezaieB.A note on the spectral characterization ofθ-graphs[J].L in A lgebra Appl,2009,431:626-632.
[8] Tan L,Zhu Z.The extremalθ-graphsw ith respect to Hosoyaindex and M errifield-S immons index[J].MA TCH Commun M ath Comput Chem,2010,63:789-798.
[9] Bollobás B.M odern graph theory[M].N ew York:Springer-V erlag,1998.
[10] Deng H.The largest Hosoya index of(n,n+1)-graphs[J].Comput M ath Appl,2008,56:2499-2506.
