潘全香,張萬(wàn)琴

一類局部共形近余辛流形的卷積子流形

潘全香,張萬(wàn)琴

(河南科技學(xué)院數(shù)學(xué)系,河南新鄉(xiāng)453003)

討論了具有常φ-截面曲率c的局部共形近余辛流形的卷積子流形,得到了其上平均曲率模長(zhǎng)‖H‖和卷積函數(shù)f的新的關(guān)系式,改進(jìn)了已有的一些結(jié)論.

常φ-截面曲率;局部共形近余辛流形;卷積子流形

B.Y.Chen在文獻(xiàn)[1]考慮實(shí)空間形式中的等距浸入卷積子流形,得到了其平均曲率模長(zhǎng)‖H‖和卷積函數(shù)f的一個(gè)關(guān)系式.

定理1 設(shè)φ:(M1×fM2)→～M(c)是具有常φ-截面曲率c的黎曼流形的卷積子流形,則有

其中ni=dimMi,i=1,2,Δ是(M1,g1)的Laplace算子.

接著,B.Y.Chen在文獻(xiàn)[2]和[3]中得到復(fù)雙曲空間和復(fù)射影空間形式中的類似結(jié)論.

隨后,D.W.Yoon在文獻(xiàn)[4]中考察具有常φ-截面曲率c的余辛空間形式的情形,得到了

定理2 設(shè)(～M(c),g;φ,ξ,η)是具有常φ-截面曲率c的余辛空間形式,(M1×fM2,g1+f2g2)是流形～M (c)中的等距浸入,而且結(jié)構(gòu)向量場(chǎng)ξ與M1相切,則

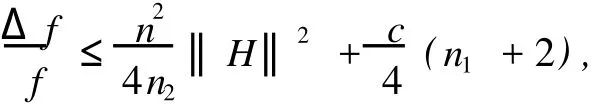
其中ni=dimMi,i=1,2,Δ是(M1,g1)的Laplace算子.

最近,B.Y.Chen和S.W.Wei在文獻(xiàn)[5]中研究了卷積流形I×fSm-1(k),分別得到了平行的曲率不變的全臍子流形和具有常曲率的超曲面的分類定理.

本文考慮ξ是具有常φ-截面曲率c的局部共形近余辛流形及流形的卷積子流形(M1×fM2,g1+f2g2)的法向量場(chǎng)的情況,得到了

定理3 設(shè)(～M(c),g;φ,ξ,η)是2m+1維的具有常φ-截面曲率c的局部共形近余辛流形,(M1×fM2, g1+f2g2)是流形～M(c)中的n維卷積子流形,而且結(jié)構(gòu)向量場(chǎng)ξ是(M1×fM2)是法向量場(chǎng),則

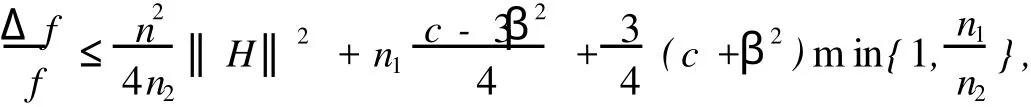
其中ni=dimMi,i=1,2,Δ是(M1,g1)的Laplace算子,β∈C∞(～M(c)).

1 預(yù)備知識(shí)

定義1 設(shè)(M1,g1),(M2,g2)的維數(shù)分別為n1,n2的黎曼流形,f是(M1,g1)上的正值函數(shù),則稱積流形(M1×fM2,g1+f2g2)為卷積(M1×fM2).

定義2 設(shè)(M×M)是M～(c)等距浸入子流形,記h為M～的第二基本形式,H=trh,其中trh是trh

1f2iii在Mi上的限制.如果對(duì)任意與M1相切的X和任意與M2相切的Y,都有h(X,Y)=0成立,則稱(M1×fM2)為混合全測(cè)地的子流形.

定義3 設(shè)(～M,g;φ,ξ,η)是近切觸度量流形.如果～M上存在1-形式ω得使dΦ=2ω Λ Φ,dη=ω Λ η,dω =0則稱～M(c)為局部共形近余辛流形.

定義4 設(shè)Mn是～M2m+1的等距浸入子流形,h為Mn的第二基本形式.如果h長(zhǎng)度的平方恒為零,即

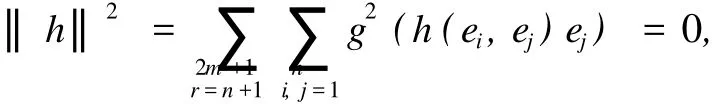
其中hrij=hr(ei,ej)=g(h(ei,ej),er),i,j∈{1,…,n},r∈{n+1,…,2m+1},則稱M是全測(cè)地的.

定義5 設(shè)φ是(～M,g)上的(1,1)型的光滑張量場(chǎng),對(duì)～M上的任一點(diǎn)p,對(duì)任意的X∈TpM,記φX=TX+ NX,其中,TX,NX分別為φX的切分量和法分量.取單位正交的切標(biāo)架場(chǎng){e1,e2,…,en,en+1,…,e2m+1}使得{e1,e2,…,en}為M的切標(biāo)架場(chǎng),{en+1,…,e2m+1}為T⊥M的標(biāo)架場(chǎng).定義T的模長(zhǎng)為

如果T恒等于零,流形M就稱為全實(shí)子流形.

為證明定理3,還需如下引理

引理1[6]設(shè)a1,…,an,an+1是n+1個(gè)實(shí)數(shù),滿足:

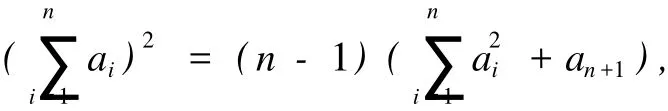
則2a1a2≥an+1,等號(hào)成立當(dāng)且僅當(dāng)a1+a2=a3=…=an.

2 定理3的證明

定理3的證明 由于(M1×fM2)是流形～M(c)中的n維卷積子流形,則由卷積流形的定義可以得到

對(duì)任意與M1相切的X和任意與M2相切的Z.

如果X,Z是單位切向量場(chǎng),則由X,Z張成的二維截面的截面曲率K(X∧Z)為

取定局部單位正交的標(biāo)架場(chǎng){e1,…,en,en+1,…,e2m+1},使得{e1,…,en1}和M1相切,{en1+1,…,en}和M2相切,en+1和H平行,e2m+1=ξ.則對(duì)任意的r∈{en1+1,…,en},由(2)式知

由Guass方程

得到:

若設(shè)

則(4)式就變成

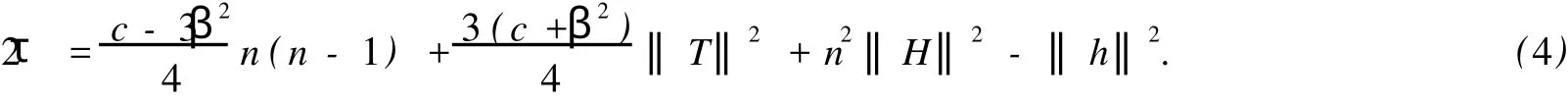
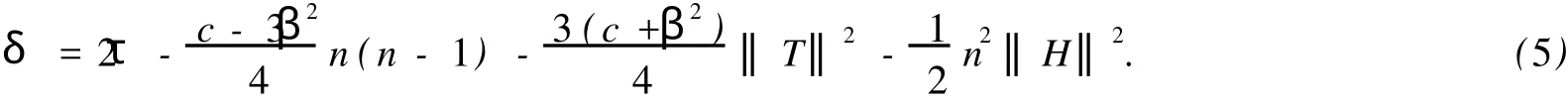
在上述所選定的標(biāo)架場(chǎng)下,(6)式就變成

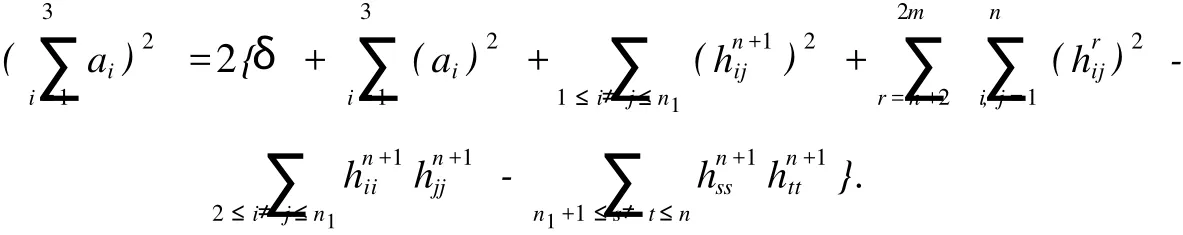
上式又可變形為

這里

再由引理1和(8)式,就有2a1a2≥b,其中等號(hào)成立當(dāng)且僅當(dāng)a1+a2=a3.此時(shí)有

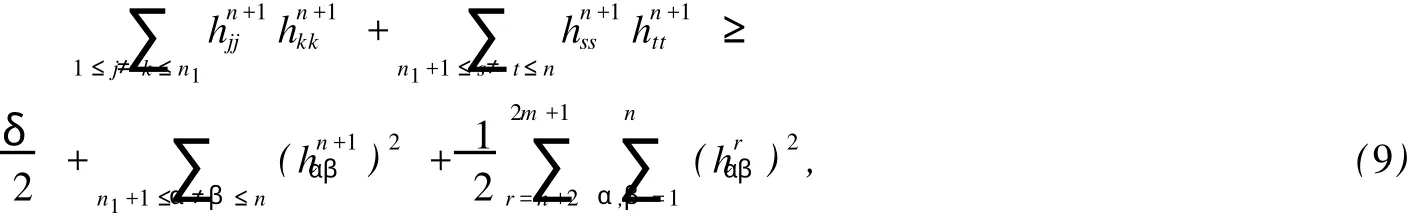
這里等號(hào)成立當(dāng)且僅當(dāng)

利用高斯方程,再結(jié)合(4)式可以得到

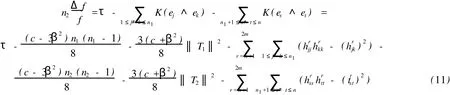
其中

由(9)式和(11)式可得

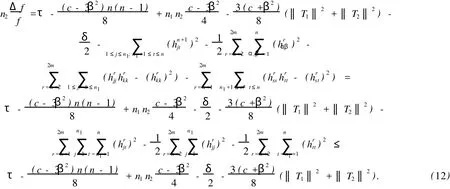
將(5)式代入(12)式,整理得

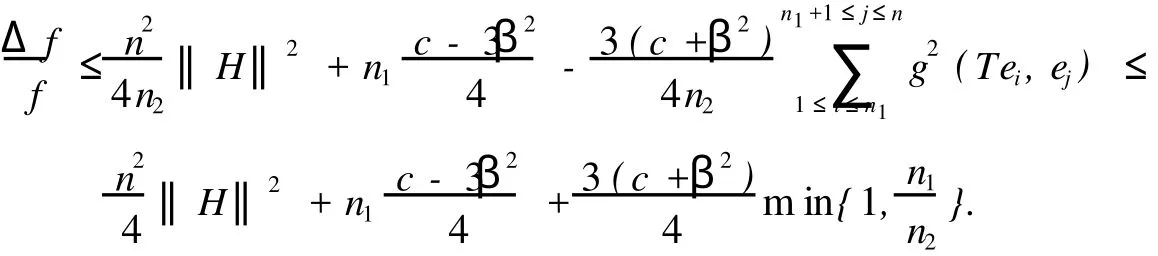
證畢.

因?yàn)棣?kenmtsu流形是局部共形近余辛流形的特殊情形,上述定理的結(jié)論對(duì)β-kenmtsu流形同樣成立.

推論1 設(shè)(～M(c),g;φ,ξ,η)是2m+1維具有常φ-截面曲率c的局部共形近余辛流形,(M1×fM2,g1+ f2g2)是流形～M(c)中的n維全實(shí)子流形,而且結(jié)構(gòu)向量場(chǎng)ξ是(M1×fM2)的法向量場(chǎng),則

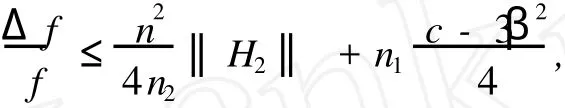
其中ni=di mMi,i=1,2,Δ是(M1,g1)的Laplace算子,β∈C∞(～M(c)).而且等式成立當(dāng)且僅當(dāng)M1×fM2是混合全測(cè)地子流形,并且n1H1=n2H2.

證明 由(5)式和定義5,再結(jié)合定理3的證明過程,易知

而且(13)中等號(hào)成立當(dāng)且僅當(dāng)

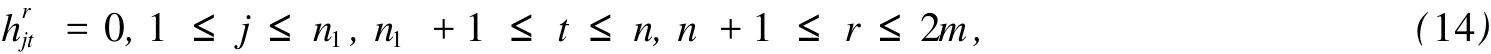
和

很明顯,(14)式等價(jià)于積流形(M1×fM2)是混合全測(cè)地的,(10)式和(15)式暗示了n1H1=n2H2.證畢.

[1] CHEN B Y.Geometry ofWarpcd Products as Riemannian Submanifolds and Related Problems[J].Soochow J M ath Soc,2002, 28:125-156.

[2] CHEN B Y.On Isomctric Minimal I mmersions from Warped Products into Real Space Forms[J].Proc Edinburgh M ath Soc, 2002,45:579-587.

[3] CHEN B Y.Non-immersion Theorems forWarped Products in Complex Hyperbolic Spaces[J].Proc Japan Acad ScrA,2002,78: 96-100.

[4] YOON D W.Some Inequality forWarped Product in Cosymplectic Space form[J].D ifferential Geom etry-Dynam ical Systems, 2004,3:51-58.

[5] CHEN B Y,WEISW.Differential Geometry of Submanifolds ofWarped ProductManifoldsI×fSm-1(k)[J].J Geom,2008,91: 21-42.

[6] 黃廣月.球面間λ2特征映射和一類近切觸度量流形的一些新結(jié)果[D].新鄉(xiāng):河南師范大學(xué),2004.

[7] 白正國(guó),沈一兵,水乃翔,郭孝英.黎曼幾何初步[M].北京:高等教育出版社,2004.

Warped Product Subman ifold of A Locally Conformal Almost CosymplecticMan ifold

PAN Quan-xiang,ZHANGWan-qin
(College ofM athematics,Henan Institute of Science and Technology,Xinxiang453003,China)

some new results are obtained on warped product submanifold of locally conformal al most cosymplectic manifold of constantφ-sectional curvaturec.It is a generalization of some existing results.

constantφ-sectional curvatrue;locally conformal al most cosymplectic manifold;warped product submanifold

O186

A

0253-2395(2010)04-0496-04

2009-09-05;

2010-01-15

河南省教育廳項(xiàng)目(2010B110011)

潘全香(1980-),女,河南浚縣人,碩士,助教,主要從事微分幾何研究.E-mail:pangguanxiang1980@163.com