The Generalized Accelerated Overrelaxation Iterative Method for Solving Large Sparse L inear Systems
Ren Fujiao Wen Ruiping
(Department of Mathematics,Taiyuan No rmal University,Taiyuan 030012,China)
The Generalized Accelerated Overrelaxation Iterative Method for Solving Large Sparse L inear Systems
Ren Fujiao Wen Ruiping
(Department of Mathematics,Taiyuan No rmal University,Taiyuan 030012,China)
A generalization of the accelerated overrelaxation(GAOR)method is p resented,which based on the new class of matrix sp littings.The remarkable feature of this new iterative method is that the method was easily implemented for parallel computation.Some theo ries of the AOR method were extended to the GAOR method.Finally,numerical examples show the advantage of thismethod.
linear system s;parallel computation;generalized AOR iterative method
0 Introduction
Let us consider iterative methods for the solution of the linear system

Sp litA=M-Nwith a nonsingular matrixM.Then the basic iterative scheme for(1)is
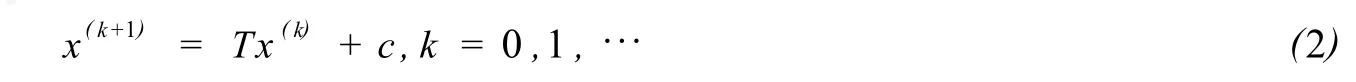
w hereT=M-1N,c=M-1b.It is well know n that the iterative method(2)convergence if and only if the spectral radiusρ(T)<1.Differentmatrix sp littings yield different iterativemethods.A sw e know n that under the sp littingA=D-L-U,w here and throughout the paperDis the(block)diagonalofAandDis nonsingular,and-Land-Uare strictly low er and strictly upper(block)triangular parts ofA,respectively.Then w e have the classical Jacobimethod,the classical Gauss-Seidelmethod,the classical SOR method and the AOR method.Detailed discussions of basic iterative methods are found in[1].
The Jacobimethod is easily imp lemented on parallel computing p latform s,but it is neither as robust no r as fast as the Gauss-Seidel method,the SOR method and the AOR method in sequential case.with p roper overrelaxation and accelerated parameters the AOR method substantially imp roves the Jacobimethod,the G-Smethod and the SOR method in term sof order imp rovement in some app lications([2~3]).The GSmethod,the SOR method and the AOR method,however,are not easily imp lemented for parallel computation because w e have to solve triangular system s at each iteration.
The aim of this paper is construct a new iterativemethod based a new classof matrix sp litting to have all advantages of the Jacobimethod and the AOR method.This paper is o rganized as follow s.First,some p reliminaries are introduced.Later,a generalization of the AOR method is p resented.The AOR theo ry on determination of the op timal parameter is extended to the new method to include a w ide class of matrices.Finally,numerical examples are p resented to corroborate the analysis.
1 Preliminaries
In this section we firstmainly introduce stairmatrices and their generalization they were first given by Lu Hao.
Def in ition1[4]A tridiagonalmatrixA=tridiag(ai,i-1,aii,ai,i+1)is called a stair matrix if one of the follow ing conditions is satisfied:

A stair matrix is of type I)if the condition I)is satisfied and is of type II)if the condition II)holds.
for convenience,a stair matrix is deno ted byA=stair(ai,i-1,aii,ai,i+1.In particular,A=stair1(ai,i-1,aii,ai,i+1)andA=stair2(ai,i-1,aii,ai,i+1)rep resent a stair matrix of type I)and a stair matrix of type II)respectively.
Def in ition2[4]Ln≡Lnn,w hereL1n={A∶Ais ann×nmatrix andA=stair(Ai,i-1,aii,ai,i+1}andLnn={A∶Ais ann×nmatrix andA=stair(Ai,i-1,Aii,Ai,i+1),w here each diagonal blockAis anni×nimatrix andAii∈Lrniw ithr<k}.
Def in ition3[2]LetA=D-P-Q,w hereDis the diagonal ofA.Assume that there is a positive integer p such that
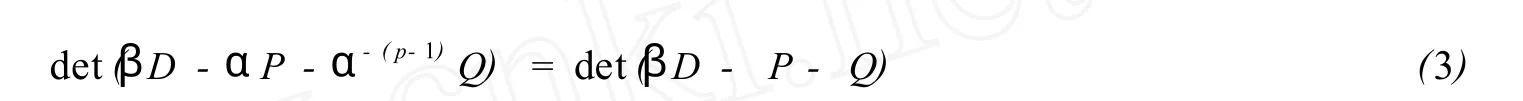
for any constantsα≠0 andβ.ThenAis called a p-consistently o rdered matrix with respect to(P,Q).
Lemma 1[1]Ann×nstair matrixA=stair(ai,i-1,aii,ai,i+1)is nonsingular if and only ifaii,i=1,2,…,nare nonsingular.Furthermo re,ifAis nonsingular,then
w hereD=diag(a11,a22,…,ann).
Theorem1[2]LetA=(aij)n×n∈Ln.ThenAH∈Ln,w hereAHis the conjugate transpose ofA,and

IfAis nonsingular,thenA-1∈Ln.
Remark1 To solve(1)w henAis a stairmatrix,the A lgorithm be first constructed in[4]and its detail p rocess of computation is discussed.Therefore,the high parallelism of A lgorithm I)in[4]is achieved ifaijare comp lex num bers o r small blocks.IfA=stair(Ai,i-1,Aii,Ai,i+1)∈Lnw e can repeatedly app ly A lgorithm I)to solve the linear systemA x=b.
2 Convergence Analysis for GAOR M ethod
A s we have seen in the p revious section the iterativemethod(2)is easily imp lemented for parallel computation ifM∈Ln.In this section,w e generalize the AOR method based on a sp littingA=M-N,w hereM∈Ln.
LetAbe ann×nmatrix with a nonsingular diagonalD.We denoteJ=I-D-1Athe Jacobimatrix ofAthroughout the paper.Sp litA=D-P-Qsuch thatP∈Ln,w here the diagonal ofPandQare zero.A generalization of the AOR(GAOR)method for the linear systemA x=bis defined by

w here here and throughout the paperSγ,ωstands for

Theorem2 LetAbe an irreducible diagonal dominancematrix,then method(6)is convergentwith 0≤γ≤1 and 0<ω≤1.
Proof Rep resentSγ,ω=(I-γP)-1[(1-ω)I+(ω-γ)D-1P+ωD-1Q]Under the condition of the Theorem 2 we findAis nonsingular with nonzero diagonalsandωD-1P∈Ln swith zero diagonals.It follow s from Theorem 1 that
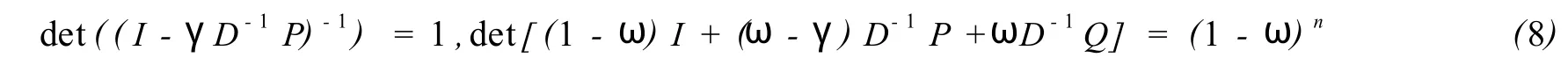
Assume that there exists any eignvalueλofSγ,ω,such that|λ| ≥1.Hence,
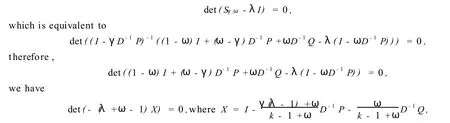
but|λ|≥1,0<ω<1,thenλ+ω-1≠0.Thus det(X)=0.
Theorem3 LetAbe anL-matrix with nonsingular diagonalD.Sp litA=D-P-Qsuch thatP∈LnandP,Qare nonnegative matrices.IfSγ,ωis defined by(7)with 0 ≤γ≤ω≤1(ω≠0),then
a)ρ(Sγ,ω)< 1 if and only ifρ(J)< 1;
b)Ais anM-matrix if and only ifρ(J)<1.
Proof Under the conditions of the theorem,D-1Pis nonnegative andD-1P∈Ln.From the Theorem 1 and using induction we find that(1-γD-1P)-1is a nonnegative matrix.The rest of the p roof is essentially the same as that of Theo rem 5.1 in[1].We delete further details.
Theorem4 LetA=D-P-Qbe a 2-constantly o rdered matrix with respect to(P,Q),w hereDis a nonsingular matrix andP∈Ln.If all the eigenvalues of theJare real,thenρ(Sγ,ω)< 1 if and only ifρ(J)<1 and 0 <ω< 2,γ1(ρ2(J))<γ<γ2(ρ2(J)).Here,γ1,γ2be defined as
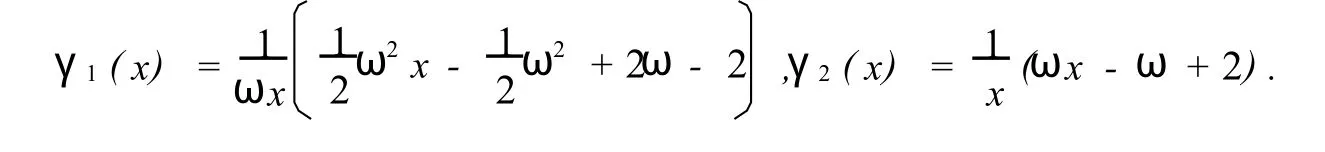
3 Numerical examples
In this section we p resent some examples to show that the new method not only is easily parallelized but also yields as fast convergence as the AOR method for a w ide class of matrices.
Exam ple1 LetA=tridiag(ai,i-1,aii,ai,i+1).ThenAis a 2-consistently ordered matrix with respect to(L,U).SplitA=D-P-Q,w here
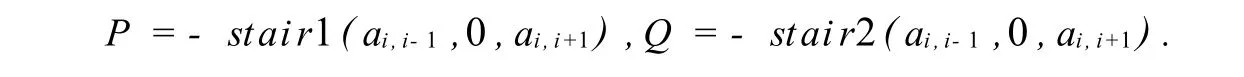
Therefore,for the linear systemA x=bthe AOR method
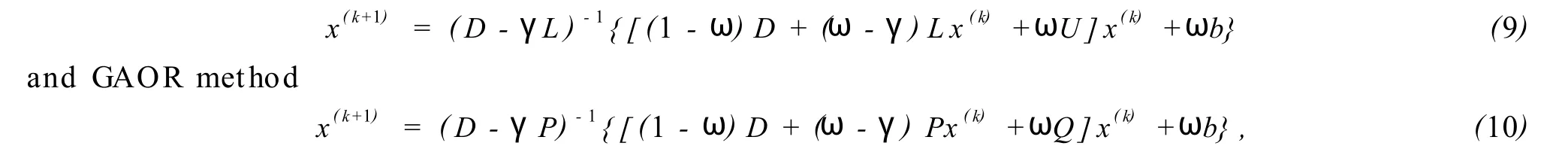
share the same op timal asymp totic rate of convergence which is taken forωandγgiven by Theorem 4,but the method(10)ismuch mo re easily imp lemented for parallel computation.
Exam ple2 Consider a 2m×2mmatrix of the form

w hereBis a 2m×2mmatrix w ithb1,2m=a1,2m,b2m,1=a2m,1,and the rest of elementsonBare all zero.We known that A is not a p-constantly ordered matrix with respect to(L,U).The theorey on determination of the op timaloverrelaxation parameter of the AORmethod is not app licable to thematricesof the form(11).How ever,if we define a 2m×2mzebra matrixPby
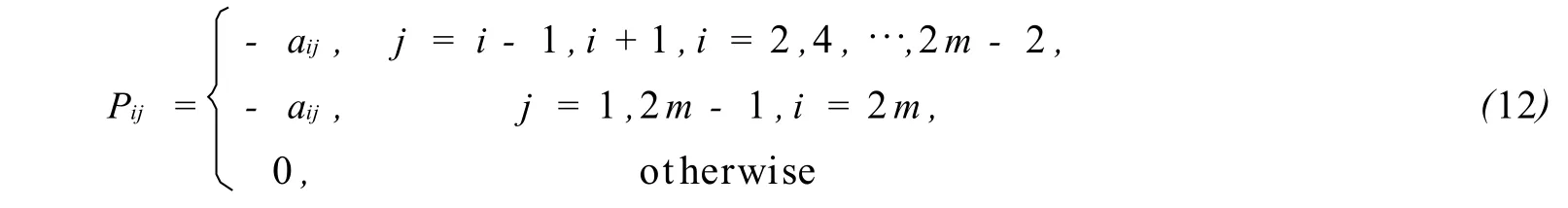
and split A=D-P-Q.Then A is a 2-constantly ordered matrix with respect to(P,Q).The Theorem 4 of this paper are still app licable for the iteration(10)if the eigenvalues of the Jacobimatrix are all real.
[1] Varga R S.Matrix iterative analysis[M].NJ:Prentice-Hall,Englewood Cliffs,1962
[2] Young D M.Iterative solution of large system[M].New York:Academic Press,1971
[3] Hackbusch W.Iterative solution of large sparse linear systems of equations[M].New York:Sp ringer-Verlag,1994
[4] Lu Hao.Stair matrices and their generalizations with applications to iterative methods I:A generalization of the successive overrelaxation method[J].SIAM J.Numer.Anal.,1999(37):1-17
2009-12-11
山西省高校重點學科建設專項資金.
任孚鮫(1963-),男,山西新絳人,太原師范學院副教授,主要從事數(shù)值代數(shù)及應用的研究.
求解大型稀疏線性方程組的廣義AOR迭代法
任孚鮫 溫瑞萍
(太原師范學院數(shù)學系,山西太原030012)
基于一種新的更一般分裂,文章提出求解大型稀疏線性方程組的廣義AOR迭代法,它的顯著特征是更易于執(zhí)行并行計算.進一步,AOR方法的一些性質相應地推廣到了新方法中.最后,用數(shù)值例子驗證了新方法的優(yōu)點.
線性方程組;并行計算;廣義AOR迭代法
【責任編輯:王映苗】
1672-2027(2010)01-0021-04
O 151.21 〔Documen t code〕 A
——生態(tài)學
- 太原師范學院學報(自然科學版)的其它文章
- 維爾斯特拉斯逼近定理的兩個推廣
- 10.7 A GeV 197 Au-Em作用電荷為3≤Z≤9的射彈碎片研究

